Demos and Proofs

April 26, 2020 Mouctar Algebra 0

Prove that:

\sqrt{a \pm \sqrt{b}}= \sqrt{\frac{a+\sqrt{a^2-b}}{2}} \pm \sqrt{\frac{a-\sqrt{a^2-b}}{2}}

While it is not allowed to drop in home works, we can still give hints when you put it in our forum.
Let b>0 and a^2-b be a square.
We will use two variables x and y to prove it.
\sqrt{a+\sqrt{b}}=\sqrt{(x+y)^2}

=\sqrt{x^2+y^2+2xy}

Now we assign the squares to a and the product to \sqrt{b}
\begin{cases}x^2+y^2=a & (1)\\2xy=\sqrt{b} & (2)\end{cases}

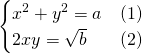
From (2) we have y=\frac{\sqrt{b}}{2x}
In (1) by substitution:
x^2+\frac{b}{4x^2}=a

After multiplication by 4x^2
4x^4-4ax^2+b=0
Let x^2=U
4U^2-4aU+b=0
\Delta=(-4a)^2-4 \times 4 \times b

=16a^2-16b

=16(a^2-b)

Now the square root of \Delta

\sqrt{\Delta}=4(\sqrt{a^2-b})

U_1=\frac{4a+4\sqrt{a^2-b}}{8}

U_1=\frac{a+\sqrt{a^2-b}}{2}

But U_1=x^2
We get:
x^2=\frac{a+\sqrt{a^2-b}}{2}

We now find the value of x

x=\sqrt{\frac{a+\sqrt{a^2-b}}{2}}

From (2) we also get y^2=a-x^2

y^2=\frac{2a-a-\sqrt{a^2-b}}{2}

y^2=\frac{a-\sqrt{a^2-b}}{2}

Please note that: \sqrt{(x+y)^2}=x+y

However, \sqrt{a+\sqrt{b}}=\sqrt{(x+y)^2}

This is what we are looking for.

If we had \sqrt{(x-y)^2}. The answer would have been: x-y

\sqrt{a-\sqrt{b}}=\sqrt{(x-y)^2}

Finally :
\sqrt{a \pm \sqrt{b}}= \sqrt{\frac{a+\sqrt{a^2-b}}{2}} \pm \sqrt{\frac{a-\sqrt{a^2-b}}{2}}

Print Friendly, PDF & Email
Post Views: 226

Be the first to comment

Leave a Reply

Your email address will not be published.


*