Algebraic identities

We have already used lot of identities in our generic problems we solved.

It is important that we learn the basic algebraic identities and how to sue them depending on the situations.
We have not studied binomials and polynomials but we can use the term binomial in these identities. For now, when we have two terms added or subtracted, let’s call it a binomial.

1. Square of a binomial

(1) $\begin{equation*} \begin{split} (a+b)^2&=(a+b)(a+b)\\ &=a^2+ab+ba+b^2\\ &=a^2+2ab+b^2 \end{split} \end{equation*}$

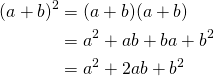
Finally:

$(a+b)^2=a^2+2ab+b^2$

The same way we get:

$(a-b)^2=a^2-2ab+b^2$

Examples:

(2) $\begin{equation*} \begin{split} (x+2)^2&=x^2+2\cdot x \cdot 2+2^2\\ &=x^2+4x+4 \end{split} \end{equation*}$

(3) $\begin{equation*} \begin{split} (3x+5)^2&=(3x)^2+2\cdot 3x \cdot 5+5^2\\ &=9x^2+30x+25 \end{split} \end{equation*}$

(4) $\begin{equation*} \begin{split} (2x-3b)^2&=(2x)^2-2\cdot 2x \cdot 3b+(3b)^2\\ &=4x^2-12bx+9b^2 \end{split} \end{equation*}$

We can also note that:

$a^2+2ab=(a+b)^2-b^2$

2. $(x+a)(x+b)$

(5) $\begin{equation*} \begin{split} (x+a)(x+b)&=x^2+bx+ax+ab\\ &=x^2+(a+b)x+ab \end{split} \end{equation*}$

$(x+a)(x+b)=x^2+(a+b)x+ab$

$(x+7)(x-3)=x^2+4x-21$

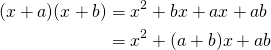
3.Difference of squares

$(a+b)(a-b)&=a^2+(b-b)a-b^2$

Or we write:

$(a+b)(a-b)=a^2-b^2$

$(3x+4y)(3x-4y)=9x^2-16y^2$

4. Square of the trinomial:

(6) $\begin{equation*} \begin{split} (a+b+c)^2&=(a+b)^2+2 \cdot (a+b)c+c^2\\ &=a^2+2ab+b^2+2ac+2bc+c^2\\ &=a^2+b^2+c^2+2ab+2ac+2bc \end{split} \end{equation*}$

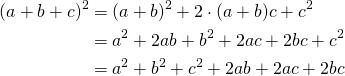
We Write:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

(7) $\begin{equation*} \begin{split} ((2x)^2+25x+7)^2&=((2x)^2)^2+(25x)^2+7^2+2 \cdot (2x)^2 \cdot 25x+2 \cdot (2x)^2 \cdot 7+2 \cdot 25x \cdot 7\\ &=16x^4+625x^2+49+200x^3+56x^2+350x\\ &=16x^4+200x^3+681x^2+350x+49 \end{split} \end{equation*}$

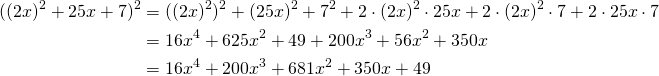
We just re-arranged the polynomial.

5.Cube of a binomial:

(8) $\begin{equation*} \begin{split} (a+b)^3&=(a+b)^2(a+b)\\ &=(a+b)(a^2+2ab+b^2)\\ &=a^3+2a^2b+ab^2+a^2b+2ab^2+b^3\\ &=a^3+3a^2b+3ab^2+b^3 \end{split} \end{equation*}$

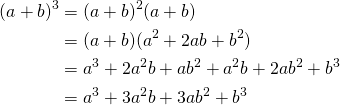
Finally we write:

$(a+b)^3=a^3+3a^2b+3ab^2+b^3$

We can also show:

$(a-b)^3=a^3-3a^2b+3ab^2-b^3$

6. Sum of cubes

If we calculate:

(9) $\begin{equation*} \begin{split} a^3+b^3&=(a+b)^3-3a^2b-3ab^2\\ &=(a+b)^3-3ab(a+b)\\ &=((a+b)^2-3ab)(a+b)\\ &=(a^2+2ab+b^2-3ab)(a+b)\\ &=(a+b)(a^2-ab+b^2) \end{split} \end{equation*}$

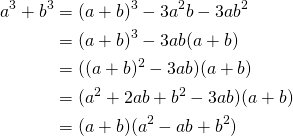
We get:

$a^3+b^3=(a+b)(a^2-ab+b^2)$

Factor: $125x^3+8y^3$

(10) $\begin{equation*} \begin{split} 125x^3+8y^3&=(5x)^3+(2y)^3\\ &=(5x+2y)(25x^2-10xy+4y^2) \end{split} \end{equation*}$

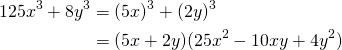
The same way we can show:

(11) $\begin{equation*} \begin{split} a^3-b^3&=(a+b)^3+3a^2b-3ab^2\\ &=(a-b)^3+3ab(a-b)\\ &=((a-b)^2+3ab)(a-b)\\ &=(a^2-2ab+b^2+3ab)(a+b)\\ &=(a-b)(a^2+ab+b^2) \end{split} \end{equation*}$

$a^3-b^3=(a-b)(a^2+ab+b^2)$

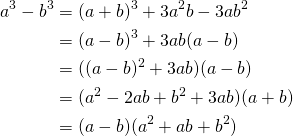
Another formula:

(12) $\begin{equation*} \begin{split} (a+b+c)^3&=\left[(a+b)+c\right]^3\\ &=(a+b)^3+3(a+b)^2c+3(a+b)c^2+c^3\\ &=a^3+3a^2b+3ab^2+b^2+3a^2c+6abc+3b^2c+3ac^2+3bc^2+c^3\\ &=a^3+b^3+c^3+3a^2b+3a^2c+3b^2a+3b^2c+3c^2a+3c^2b+6abc \end{split} \end{equation*}$