
Introduction to matrices
Introduction to Matrices
Before we start solving multiple equations, I have to introduce the matrix calculations.
Tables can be represented by what we call matrices.
A matrix is a type of rectangular array of numbers.
The dimensions of a matrix are the number of rows and columns. A matrix having 3 rows and 5 columns is called a matrix with dimensions of ![]() spelled “3 by 5”.
spelled “3 by 5”.
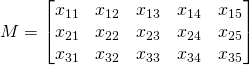
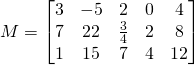
Or
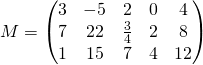
Or another valid notation:
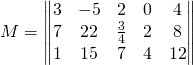
Or even
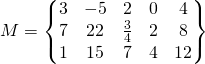
All these forms are valid and can be used. We’ll use the first one for this text.
The numbers in a matrix are called ![]() . Each element is accessed using an address.
. Each element is accessed using an address.
The element is named by the intersection of the row and the column as seen in normal spreadsheets.
If we read the element located at the third row and second column, we can that we have 15.
We can say ![]()
Comparing matrices:
Two matrices are equal when they have same dimensions with equivalent corresponding elements. Operations on matrices: Addition and subtraction: When two matrices have the same dimensions, we can add them or subtract them by merely adding or subtracting the corresponding elements.
If we have the following matrices:
![]()
![]()
We can add or subtract because they have the same dimensions ![]()
![]()
![]()
For the subtraction:
![]()
![]()
Scalar multiplication:
To multiply a matrix by a number, multiply all elements by the number:
![]()
![]()
-If we multiply a ![]() by a real number
by a real number ![]() , all elements have to be multiplied by that number.
, all elements have to be multiplied by that number.
If ![]() , the scalar multiplication will give us the
, the scalar multiplication will give us the ![]() of the original matrix.
of the original matrix.
![]()
The matrix ![]() is the
is the ![]() of matrix
of matrix ![]() .
.
Properties:
The following algebraic properties we learned apply to matrix addition:
-Commutativity: ![]()
-Additive identity : The matrix ![]() with only
with only ![]() for all elements is the identity matrix for our addition.
for all elements is the identity matrix for our addition.
-Associativity ![]()
-Finally, the additive inverse has all elements opposite to the corresponding elements of ![]()
Matrix multiplication
The golden rule in matrix multiplication is to have the following condition:
The number of columns of the first matrix must be equal to the number of rows of the second matrix.
The resulting matrix has the number of rows equal to the one of the first matrix and the number of columns equal to the one of the second matrix.
If ![]() and
and ![]() , for the multiplication to be possible we must have
, for the multiplication to be possible we must have ![]()
After the multiplication,: ![]() will be of dimensions
will be of dimensions ![]()
Process: To find an element of ![]() located at row
located at row ![]() and column
and column ![]() of
of ![]() , we have to take the sum of the products of corresponding elements in row
, we have to take the sum of the products of corresponding elements in row ![]() of
of ![]() and column
and column ![]() of
of ![]()
Example:
![]()
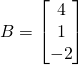
In this case :
![]() is a
is a ![]() matrix.
matrix.
![]() is a
is a ![]() matrix
matrix
The matrix product ![]() =
=![]() is a
is a ![]() matrix.
matrix.
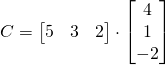
![]()
![]()
Another example
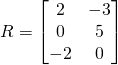
![]()
![]() is a
is a ![]() matrix.
matrix.
![]() is a
is a ![]() matrix.
matrix.
The matrix product ![]() =
=![]() is a
is a ![]() matrix.
matrix.
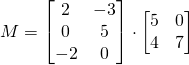
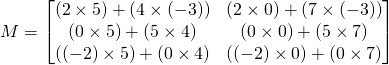
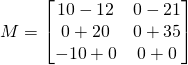
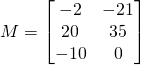
Now for bigger matrices
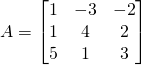
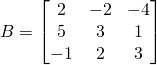
![]() is a
is a ![]() matrix.
matrix.
![]() is a
is a ![]() matrix.
matrix.
The matrix product ![]() =
=![]() is a
is a ![]() matrix.
matrix.
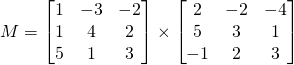
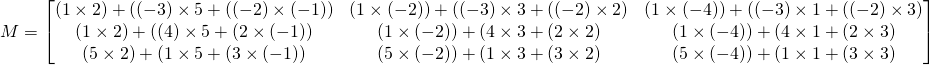
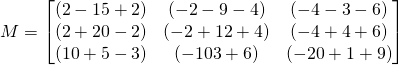
Finally:
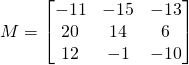
In an ![]() matrix, each element can be represented by
matrix, each element can be represented by ![]() where
where ![]() is the row of the element and
is the row of the element and ![]() is the column of the element.
is the column of the element.
What we have learned so far:
If ![]() and
and ![]() :
:
Matrix ![]() iff for every
iff for every ![]() and
and ![]() ,
, ![]()
Matrix ![]() iff for every
iff for every ![]() and
and ![]() ,
, ![]()
The ![]() noted
noted ![]() of matrix
of matrix ![]() is the matrix
is the matrix ![]()
The product of a real number ![]() and a matrix
and a matrix ![]() is equal to
is equal to ![]()
When a multiplication is possible, the matrix ![]() product of matrices
product of matrices ![]() and
and ![]() has elements
has elements ![]()
Important matrices
Matlab relies heavily on matrices manipulation.
It is important that we know some particular matrices.
Square matrix:
A square matrix is a matrix that has the same number of rows and columns.
If ![]() is a
is a ![]() matrix, we can say that
matrix, we can say that ![]() is a
is a ![]() .
.
In this case, ![]() is a matrix of order
is a matrix of order ![]() .
.
The main diagonal elements of a square matrix of order ![]() are
are ![]()
The Identity matrix
This is a square matrix noted ![]() is a matrix of order
is a matrix of order ![]() with each main diagonal element equal to
with each main diagonal element equal to ![]() and all the other elements
and all the other elements ![]() .
.
Examples
![]()
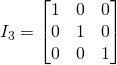
We have the following interesting fact:
![]()
Inverse of a matrix
The inverse of matrix ![]() of order
of order ![]() noted
noted ![]() , called
, called ![]() is such:
is such: ![]()
It is important to note that some matrices have no inverse or are not invertible.
We’ll see it later. Finding inverse without using ![]() may be tedious.
may be tedious.
We’ll see it on the videos that go with this refresher.
When we solve the equation ![]() , we can find the elements of
, we can find the elements of ![]()
The following example shows what I mean:
![]()
And
![]()
We can say
![]()
But ![]() since
since ![]() is of order 2.
is of order 2.
We have
![]()
![]()
![]()
![]()
![]()
We find:
![]()
Finally:
![]()
Matrix Transpose:
The transpose of a Matrix ![]() noted
noted ![]() is a new matrix whose columns are the rows of the original and making its rows, the columns of the original.
is a new matrix whose columns are the rows of the original and making its rows, the columns of the original.
If we have:
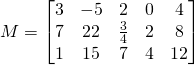
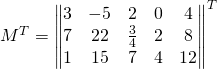
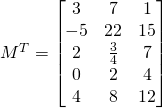
We can notice that:
![]() is a
is a ![]() matrix and
matrix and
![]() is a
is a ![]() matrix.
matrix.
We can say:
If ![]()
A small rule:
![]()
Upper and lower triangular matrices:
The diagonal of a square matrix may show two type of matrices:
-When all elements above the diagonal are zeros, we get the lower-triangular matrix.
-On the other hand, if the lower part consists of zeros, the matrix is upper-triangular
Symmetric matrix:
A symmetric matrix is a square matrix equal to its transpose.
If ![]() is symmetric, we have
is symmetric, we have ![]() =
=![]() .
.
Diagonal matrix:
A diagonal matrix is a symmetric matrix with all elements zeros but the ones on the diagonal.
Determinants: Rule of Sarrus
For 3 x 3 matrices, there is a rule called Rule of Sarrus or Sarrus’ Rule used to simplify the complicated calculations of the determinants. With this method, there is no need to calculate cofactors. There are other methods used for the 4 x 4 and above matrices. However, in this text, we will just limit our calculations to the 3 x 3 dimensions matrices.
How does it work?
We add the first column as the fourth column and we add the second column as the fifth column.
If we have a matrix:

The Determinant
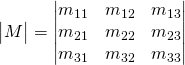
Now let’s add the two first columns:
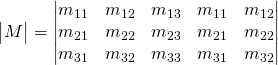
Now we take the sum of the downward diagonals of 3 elements each and we subtract the sum of the upward diagonals:


![]()
Solve using Sarrus’ Rule:
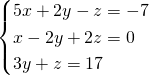
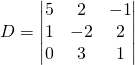

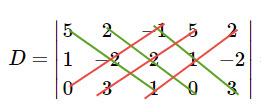
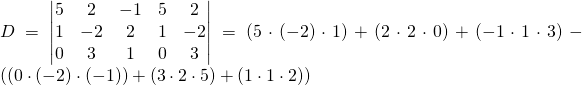
![]()
Now for ![]()
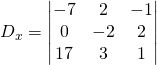
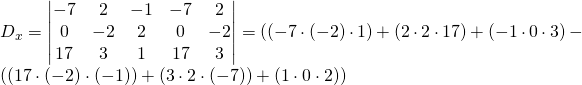
![]()
![]()
Now for ![]()
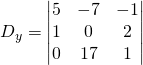
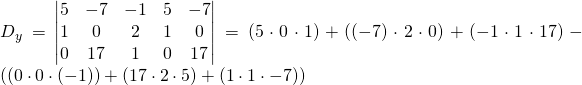
![]()
![]()
Now for ![]()
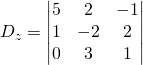
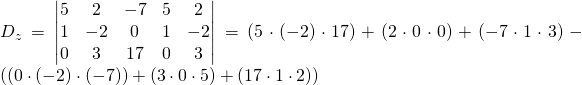
![]()
![]()
Thus, the solution is ![]()
Project Bonus: Find a number xyzuw
A number of 5 digits can be written xyzuw.
The sum of the digits is 22.
If the number is rewritten xywuz, the value increases by 297.
The digit x added to digit u and to 2 times the digits y and w, then subtracted 3 times the digit z equal 21.
Two times the digit x added to digit z then subtracted 3 times digit y and 4 times digit w equal -34.
Two times the digit u subtracted digit w and 3 times digit z equal -1.
Find the number xyzuw.
Solving by substitution:
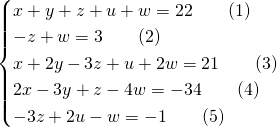
From ![]() we can write:
we can write:
![]()
![]()
From ![]() :
:
![]()
Replacing ![]() by its value of
by its value of ![]()
![]()
![]()
![]()
![]()
Now let’s subtract ![]() from
from ![]() :
:
![]()
![]()
![]()
![]()
In ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
Now we plug in everything in ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finally: Our number xyzuw is:
![]()
Using the Matrix inverse:
We get the augmented matrix
![Rendered by QuickLaTeX.com M=\left[ \begin{array}{ccccc|c} 1 & 1 & 1 & 1&1&22 \\ 0 & 0 & -1 & 0&1&3 \\1 & 2 & -3 & 1&2&21\\2 & -3 & 1 & 0&-4&-34\\0 & 0 & -3 & 2&-1&-1 \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-880a5e0d2b5b42edab03e6dadb783e5b_l3.png)
Making ![]()
![Rendered by QuickLaTeX.com M=\left[ \begin{array}{ccccc|c} 1 & 1 & 1 & 1&1&22 \\ 0 & 0 & -1 & 0&1&3 \\0 & 1 & -4 & 0&1&-1\\2 & -3 & 1 & 0&-4&-34\\0 & 0 & -3 & 2&-1&-1 \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-9a869eadbe6688593ec3128a52d47de3_l3.png)
Making ![]()
![Rendered by QuickLaTeX.com M=\left[ \begin{array}{ccccc|c} 1 & 1 & 1 & 1&1&22 \\ 0 & 0 & -1 & 0&1&3 \\0 & 1 & -4 & 0&1&-1\\2 & -3 & 1 & 0&-4&-34\\0 & 0 & 0 & 2&-4&-10 \end{array} \right]](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-fb89073da26691432bf5f34ba6e7608d_l3.png)
Finding:![]()
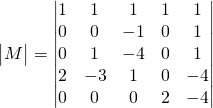
We use row 2 since we have only two values in that row:![]() is in row 2 and column 3,
is in row 2 and column 3, ![]() same for the 1 (row 2 column 5).
same for the 1 (row 2 column 5).
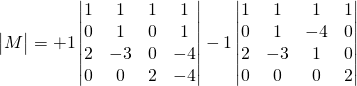
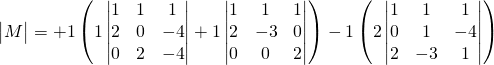
![]()
![]()
The determinant is ![]() , so we can calculate the inverse:
, so we can calculate the inverse:
The tanspose of matrix ![]() is
is
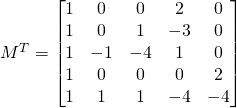
The comatrix has 25 elements, we calculate 2 elements and let the students find the rest.
For ![]() of the comatrix:
of the comatrix:
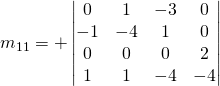
![]()
For ![]() of the comatrix:
of the comatrix:
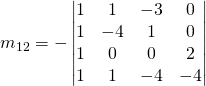
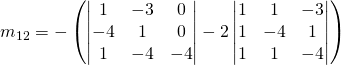
![]()
![]()
After all calculations we have:
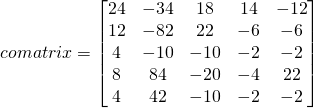
The ![]() matrix is:
matrix is:
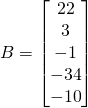
Now the solution is :
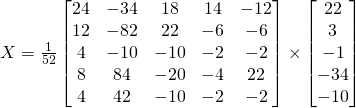
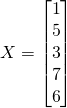
Cramer’s rule
We previously setup the solution and simplified
The student can calculate the following matrices:
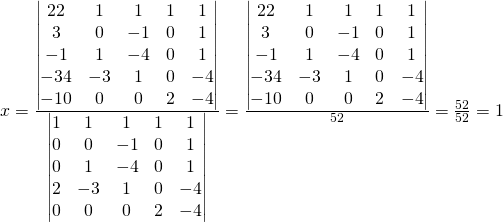
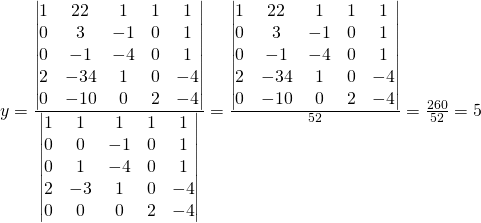
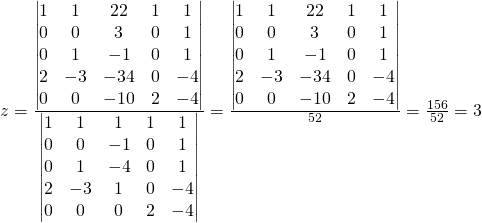
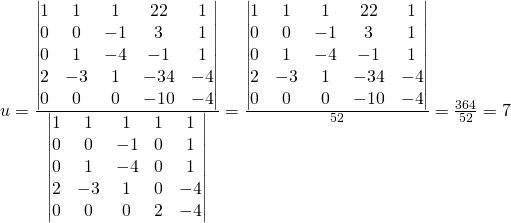
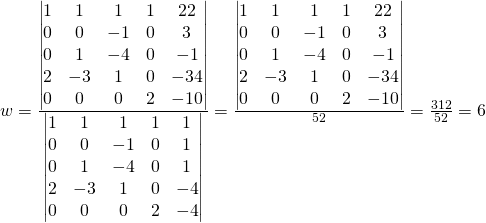
The student can practice the matrix calculation for: ![]()


Be the first to comment