

Sum and difference formulas
We have seen in the past cases where we had to use these sum and difference formulas. At this stage, we are now exploring them to be able to use them even better.
Now that we know how to identify functions of a given angle. Now we’ll see what those functions are when two angles are added and when two angles are subtracted.
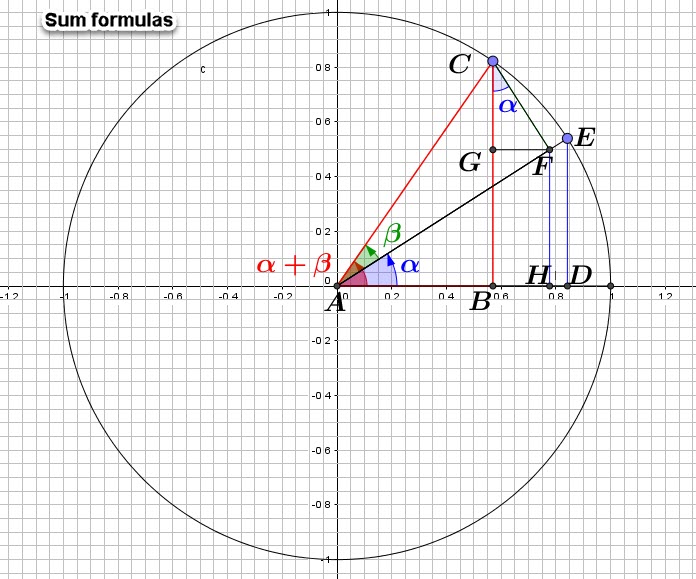
Let’s take two angles ![]() and
and ![]() and use some of well-known “postulates” fro Geometry.
and use some of well-known “postulates” fro Geometry.
Angle ![]() is in
is in ![]()
Angle ![]() is in
is in ![]()
Angle ![]() is in
is in ![]()
We know that:
![]()
But we can see that ![]()
![]()
![]()
But from ![]() we have:
we have:
![]()
From ![]() we can see that:
we can see that:
![]()
From ![]() we can see that:
we can see that:
![]()
That yields:
![]()
We can also see that: ![]()
Finally:
![]()
Sum and difference formulas using distances
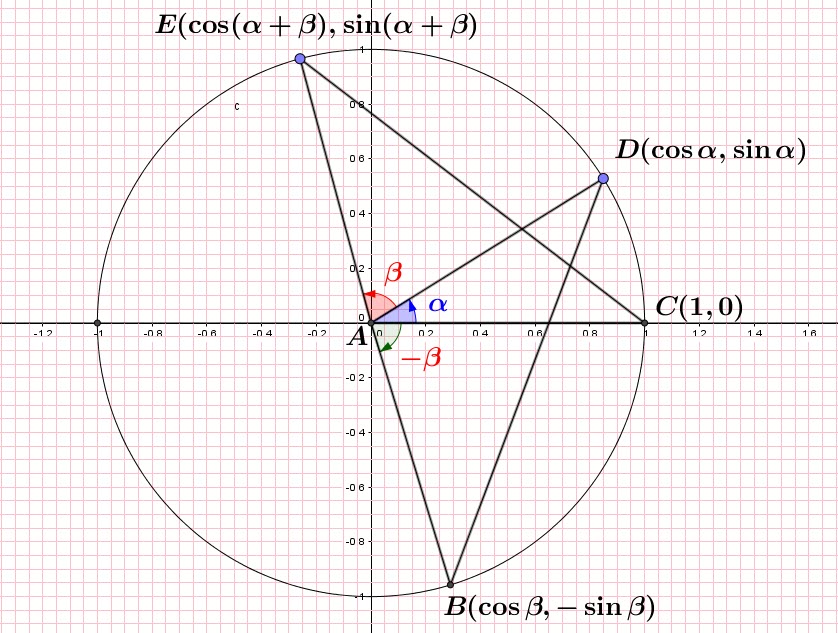
We should remember that the distance between two points is:
![]() where the coordinates pairs are
where the coordinates pairs are ![]() and
and ![]()
In the following figure:
![]()
![]() by CPCTC
by CPCTC
![]()
![]()
Simplifying:
![]()
This yields:
Using complex numbers and the de Moivre’s formula
Before we proceed, it should be noted that for two complex numbers to be equal, the real parts must be equal and the imaginary parts must be equal.
![]()
![]()
![]()
We know that ![]()
![]()
![]()
Also:
![]()
![]()
This yields:
This open the gates to a long list of trigononetric formulas that we cover in next chapters.


Be the first to comment