Formules d’addition en trigonométrie

Ce sont des formules que nous avons déjà utilisées. A ce stade, nous allons les voir plus en détails pour pouvoir les utiliser de façon plus efficace.

Nous savons trouver les fonctions trigonométriques d’un angle donné, voyons ce que ces fonctions deviennent quand des angles forment une somme ou une différence.

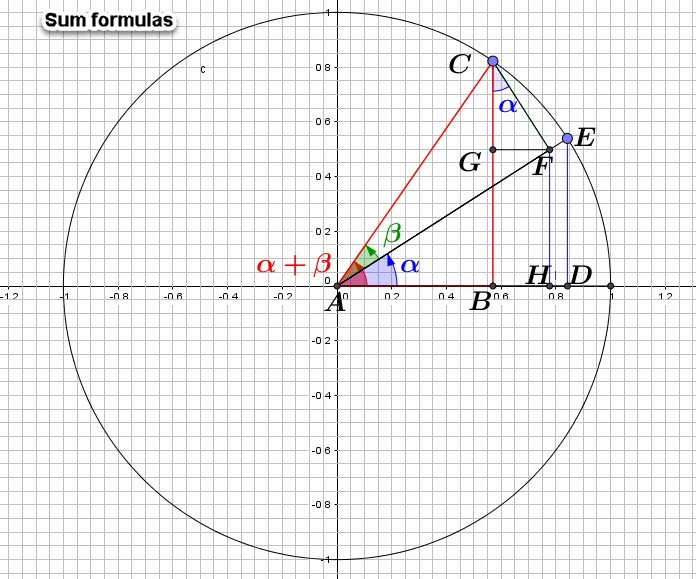
Prenons deux angles $\alpha$ et $\beta$ et servons nous de nos connaissances en géométrie.

Angle $\alpha$ est dans $\triangle DAE$

Angle $\beta$ est dans $\triangle FAC$

Angle $\alpha+ \beta$ est dans $\triangle BAC$

Nous savons que:
$\sin (\alpha+ \beta)=BC$

mais nous voyons que $BC=BG+GC$

$\cos \alpha=\frac{AH}{AF}$

$\sin \beta=FC$

Mais du triangle $\triangle GCF$ nous avons:
$\cos \alpha=\frac{GC}{FC}=\frac{GC}{\sin \beta}\Rightarrow GC=\sin \beta \cdot \cos \alpha$

De $\triangle HAF$ nous voyons que:
$\sin \alpha=\frac{HF}{AF}$

De $\triangle FAC$ nous voyons que:
$\cos \beta=AF$

Ce qui donne:
$\sin \alpha=\frac{HF}{\cos \beta} \Rightarrow HF=\sin \alpha \cdot \cos \beta$

On voit aussi que: $BG=HF$

Finalement:
$\sin (\alpha+ \beta)=BC=BG+GC=\sin \alpha \cdot \cos \beta+\sin \beta \cdot \cos \alpha$

$\sin (\alpha+\beta)=\sin {\alpha}\cos \beta+ \cos {\alpha} \sin \beta$

Formules d’addition à partir de la distance

La distance entre deux points est de:

$d=\sqrt{(X_2-X1)^{2}+(Y_2-Y1)^{2}}$ dont les coordonnées sont $(X_1,Y_1)$ et $X_2,Y_2)$

Sur la figure qui suit:

$\triangle BAD \cong \triangle CAE$

$(BD)^{2}=(CE)^{2}$ by CPCTC

$(\cos \alpha-\cos \beta)^{2}+(\sin \alpha+\sin \beta)^{2}=(\cos (\alpha+\beta)-1)^{2}+(\sin (\alpha+\beta))^{2}$

$\cos^{2} \alpha-2\cos \alpha \cos \beta+\cos^{2}\beta+ \sin^{2}\alpha+2\sin \alpha \sin \beta+\sin^{2}\beta=\cos^{2} (\alpha +\beta)-2\cos (\alpha+\beta)+1+\sin^{2} (\alpha +\beta)$

En simplifiant:
$2-2\cos \alpha \cos \beta+ 2\sin \alpha \sin \beta=-2\cos (\alpha+\beta)+2$

Ce qui donne:

$\cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta$

Utilisation des nombres complexes et de la formule de Moivre

Rappelons la condition d’égalité de deux nombres complexes:

$z=a+bi$

$z'=a'+b'i$

$a=a'\; and \; b=b' \Rightarrow z=z'$

Nous savons que $z=e^{i\alpha}=\cos \alpha+ i\sin \alpha$

$z'=e^{i\beta}=cos \beta+ i\sin \beta$

$zz'=e^{i\alpha}e^{i\beta}=e^{i(\alpha+\beta)}=\cos (\alpha+\beta)+ i\sin (\alpha+\beta)$

Aussi:

$zz'=(\cos \alpha+ i\sin \alpha)(\cos \beta+ i\sin \beta)=\cos \alpha \cos \beta+i^{2}\sin \alpha \sin \beta+i(\sin \alpha \cos \beta+\cos \alpha \sin \beta)$