Solving trigonometric equations
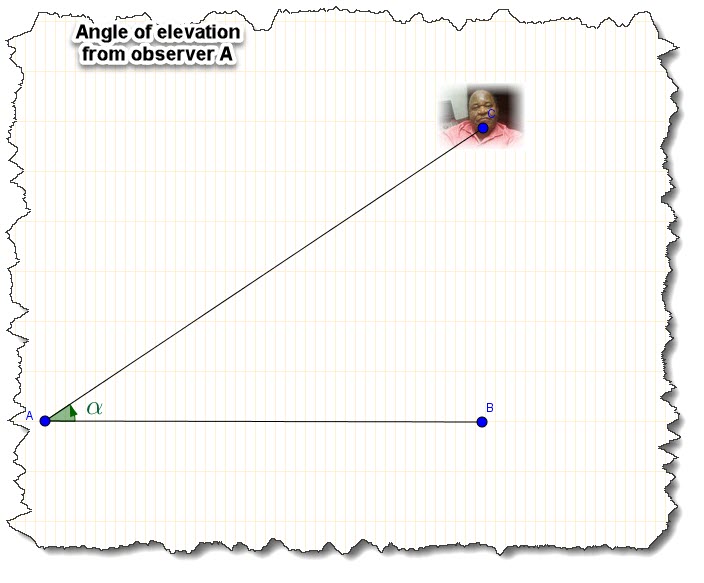
Angle of elevation:
In most trigonometric problems, you’ll see the word “Angle of elevation”.
The angle of elevation of an object is the angle formed by the horizontal and the line from that object with the vertex being the point of observation (eye of observer).
The observer looks up to see the object being observed.
In this figure ![]() or
or ![]() is the angle of elevation.
is the angle of elevation.
Angle of depression:
IThe angle of depression of an object is the angle formed by the horizontal and the line from that object with the vertex being the point of observation (eye of observer).
If you look at the figure, in this situation the observer is at a level higher that the one of the object. The observer looks down to see the object being observed.
In this figure ![]() or
or ![]() is the angle of depression.
is the angle of depression.

Right triangle Formulas
We have already seen these for the unit circle.
The challenge here is that our hypotenuse may never be ![]() .
.
We can,however,divide all the sides, including the hypotenuse, by the hypotenuse and we get:
For a non-right angle in the triangle:
![]() for the unit circle.
for the unit circle.
![]() for the unit circle.
for the unit circle.
These two formulas become:
The tangent remains unchanged:
Most of the elementary trigonometry problems will be solved using these formulas.
We can see now why we should create a right angle for any given problem, where that can help, and solve using these simple formulas.
Inverse trigonometric functions:
Our trigonometric functions being one-to-one functions, we can find their inverse functions.
Those functions are of the form:
If ![]() , we can reverse the correspondence and get
, we can reverse the correspondence and get ![]() .
.
We will have a special chapter on inverse functions.
For ![]() we have:
we have:
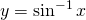 for
for 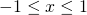 and
and 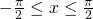
We have the property:
![]() if
if ![]()
![]() if
if ![]()
Example:
Find ![]() for:
for:
![]()
![]()
![]()
For ![]() we have:
we have:
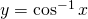 for
for 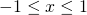 and
and 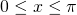
Please read “y is the inverse cosine of x” or arccosine
We have the property:
![]() if
if ![]()
![]() if
if ![]()
For ![]() we have:
we have:
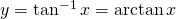 iff
iff 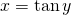
for any 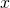 and for
and for 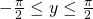
Please read “y is the inverse tangent of x” or arctangent
We have the property:
![]() for every
for every ![]()
![]() if
if ![]()
Example:
Find the value of:
if ![]() we can have
we can have ![]()
The hypotenuse here is ![]() .
.
Now :
![]()
![]()
if ![]() we can have
we can have ![]()
The hypotenuse here is ![]() .
.
Now :
![]()
All we need is ![]()
![]()
After simplification we have:
![]()


Be the first to comment