Latest Topics

Formules trigonométriques et identités

December 16, 2016 Mouctar Trigonometry 0

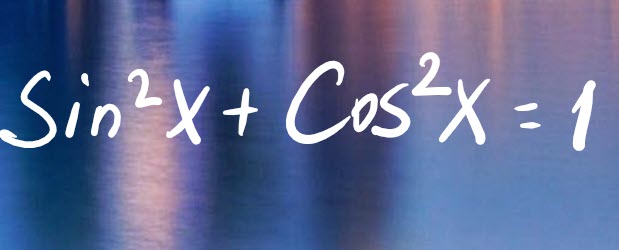
trigo1

Formules trigonométriques et identités

Nous avons pratiquement pris connaissance de beaucoup de formules trigonométriques. Il est temps de les mettre sur une liste et commencer à nous préparer dans la résolution des problèmes.

Dans certains des cas, nous allons ajouter des détails montrant comment nous sommes parvenus à certaines formules. des vidéos pourraient y figurer.

Trigonométrie du triangle rectangle

Pour un triangle ABC, rectangle en $C$ , $\angle C=90^{\circ}$

$\cos A=\frac{adjacent side}{hypotenuse}=\frac{1}{\sec A}$

$\sin A=\frac{opposite side}{hypotenuse}=\frac{1}{\csc A}$

$\tan A=\frac{opposite side}{adjacent \;side}=\frac{1}{\cot A}=\frac{\sin A}{\cos A}$

$\sec A=\frac{hypotenuse}{adjacent \; side}=\frac{1}{\cos A}$

$\csc A=\frac{hypotenuse}{opposite \;side}=\frac{1}{\sin A}$

$\cot A=\frac{adjacent side}{opposite \;side}=\frac{1}{\tan A}=\frac{\cos A}{\sin A}$

Ces relations sont connues. On ne fera que diviser les trois côtés du triangle par l’hypothenuse pour avoir le cercle trigonométrique de $rayon=1$ , l’hypothenuse.

Loi des cosinus

Pour un triangle quelconque:

${a}^2={b}^2+{c}^2-2 \cdot b \cdot c\cdot\cos{A}$

${b}^2={a}^2+{c}^2-2 \cdot a \cdot c\cdot\cos{B}$

${c}^2={a}^2+{b}^2-2 \cdot a \cdot b\cdot\cos{C}$

Loi des sinus

$\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}$

Autres identités

$\sin^{2} A+ \cos^{2} A=1$

We can easely show:

$1+\tan^{2} A= \sec^{2} A$

$1+\cot^{2} A= \csc^{2} A$

On peut facilement retrouver toutes ces formules sur le cercle unitaire.

Angles complémentaires:

Si $A$ et $B$ sont des angles complémentaires $sum=90^{\circ}$ :

$B=90^{\circ}-A$

$\sin A=\cos B$

$\sin B=\cos A$

$\sec A= \csc B$

$\sec B= \csc A$

$\tan A= \cot B$

$\tan B= \cot A$

Formules d’addition et de soustraction

$\sin (A+B)=\sin {A} \cos{B}+\cos {A} \sin {B}$

$\sin (A-B)=\sin {A} \cos{B}-\cos {A} \sin {B}$

$\cos (A+B)=\cos {A} \cos{B}-\sin {A} \sin {B}$

$\cos (A-B)=\cos {A} \cos{B}+\sin {A} \sin {B}$

On les utilise pour trouver

$\tan {(A+B)}=\frac{\tan {A}+ \tan {B}}{1-\tan {A} \tan{B}}$

$\tan {(A-B)}=\frac{\tan {A}- \tan {B}}{1+\tan {A} \tan{B}}$

Angles doubles

From above when $B=A$

$\sin {2A}=2\sin {A} \cos{A}$

$\cos {2A}=\cos^{2}A-\sin^{2}A$

$\tan {2A}=\frac{2\tan A}{1-\tan^{2} A}$

Arc-moitié

Quand $B=A$

$\sin {\frac{A}{2}}=\pm \sqrt{\frac{1-\cos A}{2}}$

$\cos {\frac{A}{2}}=\pm \sqrt{\frac{1+\cos A}{2}}$

$\tan {\frac{A}{2}}=\frac{1-\cos A}{\sin A}=\frac{\sin A}{1+\cos A}$

Product à somme

Des formules précédentes :

$\sin {A} \cos{B}=\frac{1}{2}(\sin (A+B)+\sin (A-B) )$

$\cos {A} \sin{B}=\frac{1}{2}(\sin (A+B)-\sin (A-B) )$

$\cos {A} \cos{B}=\frac{1}{2}(\cos (A+B)+\cos (A-B) )$

$\sin {A} \sin{B}=\frac{1}{2}(\cos (A-B)-\cos (A+B) )$

Somme à produit

$\sin {A} + \sin{B}=2\sin {\frac{A+B}{2}}\cos {\frac{A-B}{2}}$

$\sin {A} - \sin{B}=2\cos {\frac{A+B}{2}}\sin {\frac{A-B}{2}}$

$\cos {A} + \cos{B}=2\cos {\frac{A+B}{2}}\cos {\frac{A-B}{2}}$

$\cos {A} - \cos{B}=-2\sin {\frac{A+B}{2}}\sin {\frac{A-B}{2}}$

Post Views: 798

Leave a Reply Cancel reply

Mouctar.org 2023, All Rights Reserved