
Solutions of the cubic Function
We have already discussed most of it in our polynomials discussion.
The following discussion takes care of all possible values of the solution when we are facing a problem involving the cubic function.
Given:
![]()
Let’s depress the equation.
![]()
We apply the substitution
![]()
![]()
![]()
![]()
We simplify:
![]()
We factor like terms and eliminate cancelling terms:
![]()
![]()
Dividing by ![]() we can let:
we can let:
![]()
and
![]()
We get the deprecated function.
![]()
Please note that when ![]() , we can simply deduct the 3 values of
, we can simply deduct the 3 values of ![]() from those of
from those of ![]() .
.
This situation is ideal because the term in ![]() has vanished.
has vanished.
Let:
![]()
We get
![]()
![]()
![]()
We can see that :
![]() and
and ![]() will make our equation
will make our equation ![]() .
.
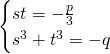
Let’s cube the first line:
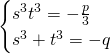
Now let:
![]() and
and ![]()
We get:
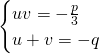
To solve this we’ll use:
![]()
If ![]() , the equation has one real root and 2 complex roots
, the equation has one real root and 2 complex roots
If ![]() , the equation has one root
, the equation has one root ![]() and a double root
and a double root ![]()
If ![]() , the equation has three real roots
, the equation has three real roots
Case 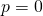
![]()
We have complex roots:
![]()
![]()
![]() with
with ![]()
If ![]()
We get:
![]()
![]()
![]()
![]()
Case 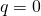
![]()
![]()
![]()
if ![]()
![]()
![]()
![]()
![]()
![]()
if ![]()
![]()
![]()
![]()
![]()
![]()
Case 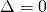
![]()
This means:
![]() Meaning
Meaning ![]()
We get the following solutions:
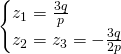
We use
![]() to get
to get ![]()
Case 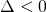
We proceed as follows:
![]()
When we replace ![]() in our equation:
in our equation:
![]()
![]()
![]()
![]()
By simple division we get:
![]()
Let’s simplify the left side:
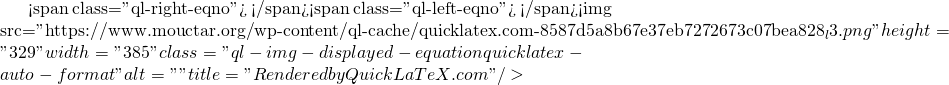
From this we get:
![]()
If we let :
![]()
From our main equation:
![]()
Replacing from above
![]()
![]()
The same technic we used earlier helps us get
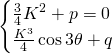
With ![]()
![]()
![]()
The simplified Equation is:
![]() Remember
Remember ![]()
![]() with
with ![]()
Our Solutions:
![]()
![]()
![]()
We can now find ![]() .
.
![]()
![]()
![]()
Case 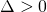
when 
Here we say:
![]()
The same transformations yield:
![]()
And:
![]()
when 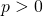
Here we say:
![]()
The same transformations yield:
![]()
And:
![]()
General rule for all solutions including the complex conjugates:
From
![]()
With:
![]()
First case: when 
Let’s calculate ![]() and
and ![]()
![]()
Now:
![]()
The ![]() values:
values:
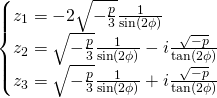
For ![]() values we just apply
values we just apply ![]()
Second case: when 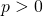
Let’s calculate ![]() and
and ![]()
![]()
Now:
![]()
The ![]() values:
values:
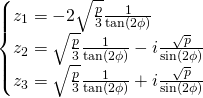
For ![]() values we just apply
values we just apply ![]()
Example 1:
Find the solutions of the following equation:
![]()
Solution:

Instead of using multiple tries between 72 and 10 and their factors, we are going to use the methods learned here.
To avoid big numbers, let’s divide the function by 10.
We get
![]()
We have the following coefficients:
![]()
![]()
![]()
![]()
Let’s calculate ![]() and
and ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Both values were left at their fractions forms to avoid accuracy loss.
Now:
![]()
![]()
![]()
We are in the case where ![]()
We call our method to get the 3 real roots:
![]()
![]()
![]() in degrees
in degrees
![]()
![]()
![]()
The solutions:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finally the solutions are:
Answer: ![]() ,
, ![]() and
and ![]()
Example 2:
Find the solutions of the following equation:
![]()
Solution:

Instead of using multiple tries between 4 and 50 and their factors, we are going to use the methods learned here.
To avoid big numbers, let’s divide the function by 50.
In future exercises, we’ll use simplest methods.
We get:
![]()
We have the following coefficients:
![]()
![]()
![]()
![]()
Let’s calculate ![]() and
and ![]()
![]()
![]()
We plug in:
![]()
![]()
![]()
The exponent ![]() vanishes
vanishes
![]()
![]()
Here:
![]()
![]()
Let’s check on ![]()
![]()
![]()
![]()
We are in the case where ![]()
We get the following solutions:
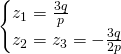
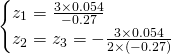
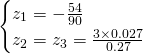
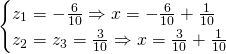
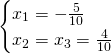
Finally the solutions are:
Answer: ![]() ,
, ![]() and
and ![]()
Example 3:
Find the solutions of the following equation:
![]()
Solution:

Instead of using multiple tries between 6 and 1 and their factors, we are going to use the methods learned here.
In future exercises, we’ll use simplest methods.
We have the following coefficients:
![]()
![]()
![]()
![]()
Let’s calculate ![]() and
and ![]()
![]()
![]()
We plug in:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If ![]() , the equation has one real root and 2 complex roots
, the equation has one real root and 2 complex roots
![]()
Let’s calculate ![]() and
and ![]()
![]()
![]()
![]()
Now:
![]()
![]()
![]()
The ![]() values:
values:
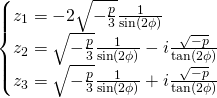
For the ![]() values:
values:
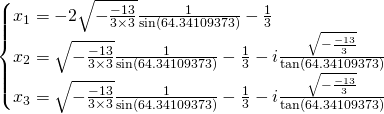
We get:
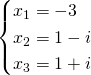
Finally the solutions are:
Answer: ![]() ,
, ![]() and
and ![]()
Atlernate methods using division
The following documents show how the division can get the factors, reducing the cubic function to a product that we normally solve:
Example 1:
Find the solutions of the following equation:
![]()
Solution:
[accordion hideSpeed=”300″ showSpeed=”400″][accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Click here to see the solution of: ![]() “]
“]
{aridoc engine=”pdfjs” width=”100%” height=”800″}images/Alternate2.pdf{/aridoc}
[/item] [/accordion]
Example 2:
Find the solutions of the following equation:
![]()
Solution:
[accordion hideSpeed=”300″ showSpeed=”400″][accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Click here to see the solution of:![]() “]
“]
{aridoc engine=”pdfjs” width=”100%” height=”800″}images/Alternate1.pdf{/aridoc}
[/item] [/accordion]
Example 3:
Find the solutions of the following equation:
![]()
Solution:
[accordion hideSpeed=”300″ showSpeed=”400″][accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Click here to see the solution of:![]() “]
“]
{aridoc engine=”pdfjs” width=”100%” height=”800″}images/Alternate3.pdf{/aridoc}
[/item] [/accordion]
HELPER FUNCTION
Open this using the right box with pointing arrow and select ‘OPEN WITH GOOGLE SHEETS’ to solve more cubic equations.
![]()
{aridoc engine=”google” width=”100%” height=”800″}images/cubic1.xlsx{/aridoc}

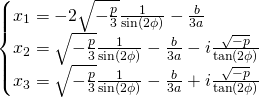
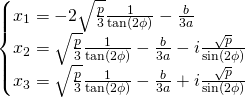

Be the first to comment