Introduction to Conic Sections
Conic sections can be generated when one slanted line revolves around an intersecting a vertical line . We get two cones joined at the intersection and expading indefinitely upward and downward.
When a plane intersects the created double cone, we have a conic section at the intersection.
Depending on how the plane is intersecting the conic section, we get different types of conic sections.
The conic sections may be : parabola, ellipse, hyperbola, circle etc…
The following is a summary to enable us to solve problems involving the conic sections.
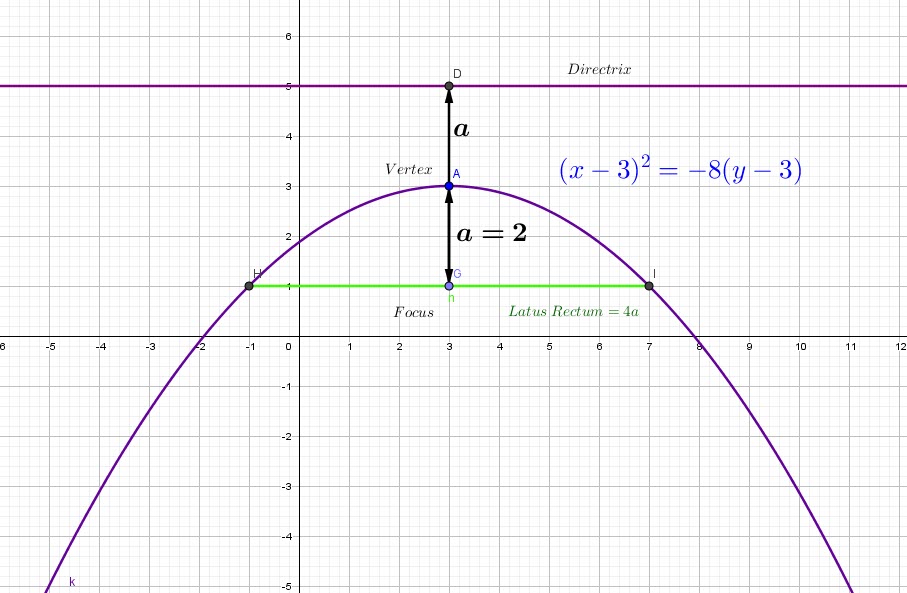
The Parabola:
A parabola can be defined as the collection of all points ![]() in the plane that are the same distance
in the plane that are the same distance ![]() from a fixed point
from a fixed point ![]() as they are from another fixed line
as they are from another fixed line ![]() .
.
The point ![]() is called the
is called the ![]()
The line ![]() is the
is the ![]() .
.
![]()
The line through the focus ![]() and perpendicular to the directrix
and perpendicular to the directrix ![]() is the
is the ![]() .
.
The point of intersection of the parabola and its axis of symmetry is the ![]() , noted
, noted ![]() .
.
If we take a VERTEX at ![]() , with FOCUS at
, with FOCUS at ![]() while
while ![]() , by definition the DIRECTRIX will be the line
, by definition the DIRECTRIX will be the line ![]() .
.
Using the definition above and the distance formula:
![]()
Solving we get:
Equation of the parabola:
![]()
The LATUS RECTUM here has a length of ![]() and is defined as the line segment joining
and is defined as the line segment joining ![]() and
and ![]()
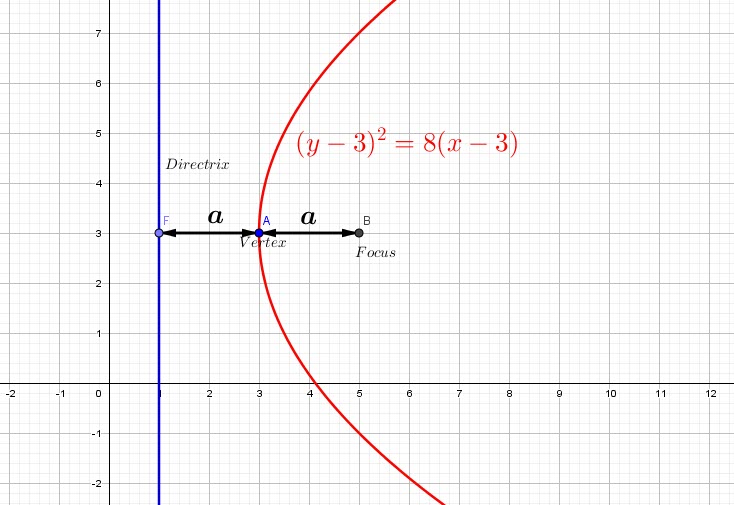
We get the following cases: for a VERTEX at (h,k):
-When for vertex ![]() we have a focus
we have a focus ![]() , the DIRECTRIX will be the line
, the DIRECTRIX will be the line ![]() and the equation is
and the equation is ![]() Symmetry axis is parrallel to
Symmetry axis is parrallel to ![]() , opens right.
, opens right.
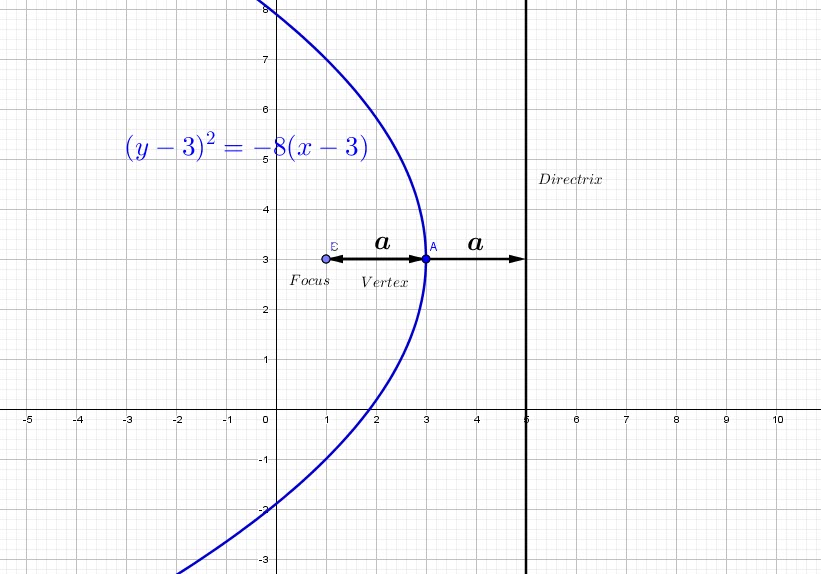
-When for vertex ![]() we have a focus
we have a focus ![]() , the DIRECTRIX will be the line
, the DIRECTRIX will be the line ![]() and the equation is
and the equation is ![]() Symmetry axis is parrallel to
Symmetry axis is parrallel to ![]() , opens left.
, opens left.
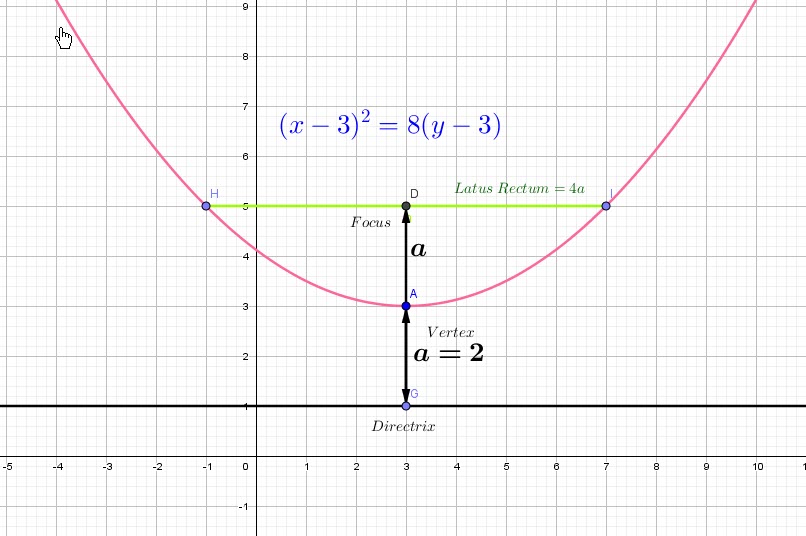
-When for vertex ![]() we have a focus
we have a focus ![]() , the DIRECTRIX will be the line
, the DIRECTRIX will be the line ![]() and the equation is
and the equation is ![]() Symmetry axis is parrallel to
Symmetry axis is parrallel to ![]() , opens up.
, opens up.
-When for vertex ![]() we have a focus
we have a focus ![]() , the DIRECTRIX will be the line
, the DIRECTRIX will be the line ![]() and the equation is
and the equation is ![]() Symmetry axis is parrallel to
Symmetry axis is parrallel to ![]() , opens down.
, opens down.
We get the following cases: for a VERTEX at (0,0):
-When for vertex ![]() we have a focus
we have a focus ![]() , the DIRECTRIX will be the line
, the DIRECTRIX will be the line ![]() and the equation is
and the equation is ![]() Symmetry axis is
Symmetry axis is ![]() , opens right.
, opens right.
-When for vertex ![]() we have a focus
we have a focus ![]() , the DIRECTRIX will be the line
, the DIRECTRIX will be the line ![]() and the equation is
and the equation is ![]() Symmetry axis is
Symmetry axis is ![]() , opens left.
, opens left.
-When for vertex ![]() we have a focus
we have a focus ![]() , the DIRECTRIX will be the line
, the DIRECTRIX will be the line ![]() and the equation is
and the equation is ![]() Symmetry axis is
Symmetry axis is ![]() , opens up.
, opens up.
-When for vertex ![]() we have a focus
we have a focus ![]() , the DIRECTRIX will be the line
, the DIRECTRIX will be the line ![]() and the equation is
and the equation is ![]() Symmetry axis is
Symmetry axis is ![]() , opens down.
, opens down.
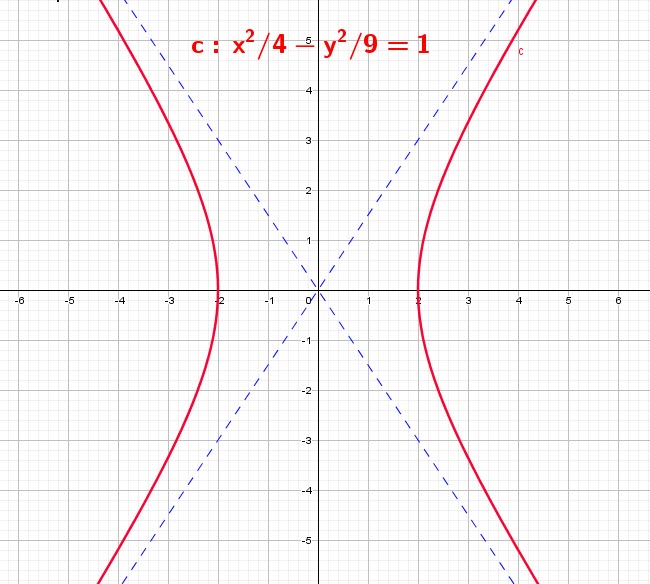
The Hyperbola:
A hyperbola can be defined as the collection of all points ![]() in the plane, haveing a difference of distances from two points,
in the plane, haveing a difference of distances from two points, ![]() as constant.
as constant.
The line containing the Foci is the ![]() .
.
The ![]() of the hyperbola is the midpoint of the segment joining the
of the hyperbola is the midpoint of the segment joining the ![]() .
.
The perpendicular of the transverse axis trhough the center is called the ![]() .
.
The two separate curves of the hyperbola are the ![]()
The points of intersection of the hyperbola and the transverse axis are the ![]() of the hyperbola.
of the hyperbola.
If ![]() ,
, ![]() with
with ![]() the distance between a focus and the center.
the distance between a focus and the center.
For any given point ![]() , we can have:
, we can have:
![]()
Using the distance formula:
In this equation we have ![]()
![]()
![]()
Let’s square both sides:
![]()
We simplify:
![]()
Simplifying by 4
![]()
![]()
Let’s square both sides again:
![]()
![]()
![]()
![]()
![]()
Let: ![]()
We get:
![]()
Now dividing both sides by ![]()
We have the hyperbola formula:
![]()
The transverse axis here is the ![]()
Asymptotes:
We’ll see in future chapters how to calculate the limits.
However, if we take:
![]()
When ![]() approaches infinity (left or right side), the value
approaches infinity (left or right side), the value ![]() approaches
approaches ![]()
we get:
![]() and
and ![]()
These are the two oblique asymptotes:
![]() and
and ![]()
For the hyperbola of Center at ![]() ; The transverse Axis along the
; The transverse Axis along the ![]()
Foci are at ![]() and
and ![]() ,
,
and vertices at ![]() and
and ![]()
![]()
Asymptotes:
We’ll see in future chapters how to calculate the limits.
However, if we take:
![]()
When ![]() approaches infinity (left or right side), the value
approaches infinity (left or right side), the value ![]() approaches
approaches ![]()
we get:
![]() and
and ![]()
These are the two oblique asymptotes:
![]()
and
![]()
Hyperbola Equations:
Transverse parallel to the ![]()
Center ![]()
Foci: ![]()
Vertices: ![]()
Equation:
![]()
![]()
Asymptotes:
![]()
Transverse parallel to the ![]()
Center ![]()
Foci: ![]()
Vertices: ![]()
Equation:
![]()
![]()
Asymptotes:
![]()
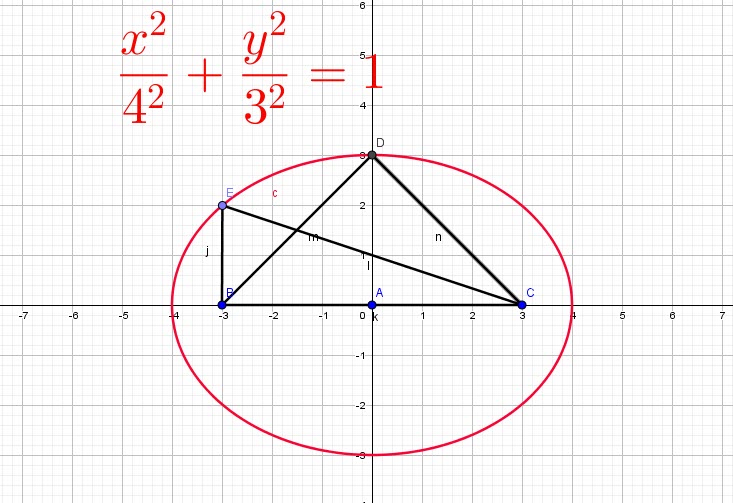
The ELLIPSE:
The Ellipse can be defined as the collection of all points ![]() in the plane, having a sum of distances from two points,
in the plane, having a sum of distances from two points, ![]() as constant.
as constant.
The line containing the Foci is the ![]() .
.
The ![]() of the ellipse is the midpoint of the segment joining the
of the ellipse is the midpoint of the segment joining the ![]() .
.
The perpendicular of the major axis trhough the center is called the ![]() .
.
The points of intersection of the ellipse and themajor axis are the ![]() of the ellipse.
of the ellipse.
If ![]() and
and ![]() ,
, ![]() is the constant distance: Point
is the constant distance: Point ![]()
Using the same technic we used for the Hyperbola:
![]()
![]() where
where ![]()
The major axis here is along the ![]()
For the Ellipse of Center at ![]() ; The major Axis along the
; The major Axis along the ![]()
Foci are at ![]() and
and ![]() ,
,
and vertices at ![]() and
and ![]()
![]() where
where ![]()
![]()
Ellipse Equations:
Major axis parallel to the ![]()
Center ![]()
Foci: ![]()
Vertices: ![]()
Equation:
![]()
![]()
Major axis parallel to the ![]()
Center ![]()
Foci: ![]()
Vertices: ![]()
Equation:
![]()
![]()
The Circles
A circle is the set of all points in a plane that are equidistant from a given point in the plane, ![]()
The distance from any point to the center is ![]() .
.
For a circle of center ![]() .
.
For a point ![]()
The radius ![]() can be found using the distance formula;
can be found using the distance formula;
![]()
We square both sides:
![]()
The Equation of the circle of center ![]()
![]()
The tangent is perpendicular to the radius at the tangency point.
For more details see our course on CIRCLE ESSENTIALS.
Conics, general equation
Conics can be identified using the general equation when we do not have a degenerating case:
![]() and
and ![]() cannot both equal
cannot both equal ![]()
When ![]() , we have a PARABOLA
, we have a PARABOLA
When ![]() we have an ELLIPSE (or CIRCLE)
we have an ELLIPSE (or CIRCLE)
When ![]() , it is a hyperbola
, it is a hyperbola
We can also use the following rule to identify a conic:
When we do not have a degenerating case:
When ![]() , we have a PARABOLA
, we have a PARABOLA
When ![]() we have an ELLIPSE (or CIRCLE)
we have an ELLIPSE (or CIRCLE)
When ![]() , it is a hyperbola
, it is a hyperbola
Conics in polar Equations
In this passage, we are going to express the conics dicussed above, using their polar notations.
For a given Conic, we will call the line ![]() the
the ![]() ,
, ![]() a given
a given ![]() .
.
In our new notation, let’s introduce ![]() as a fixed positive number, the
as a fixed positive number, the ![]() .
.
A ![]() is then the set of points
is then the set of points ![]() such the ratio of the distance
such the ratio of the distance ![]() to the distance
to the distance ![]() is
is ![]() .
.
– For the parabola, we can note that ![]()
-For the ellipse we have ![]()
-For the hyperbola ![]()
If ![]() is the distance from the center to the focus and
is the distance from the center to the focus and ![]() is the distance from the center to the vertex, for ellipse and hyperbola:
is the distance from the center to the vertex, for ellipse and hyperbola:
Each point ![]() can be expressed in polar coordinates as
can be expressed in polar coordinates as ![]()
![]()
If we drop a perpendicular from ![]() to the polar axis with
to the polar axis with ![]() as intersection, we can write:
as intersection, we can write:
![]()
But we can see that ![]()
We can plug in:
![]()
![]()
Solving for ![]() we get:
we get:
The polar equation of a Conic:
With ![]() the eccentricity of the conic.
the eccentricity of the conic.
If the ![]() is perpendicular to the polar-axis at a distance
is perpendicular to the polar-axis at a distance ![]() on the right of the pole:
on the right of the pole:
we get:
SUMMARY
1. Directrix perpendicular to the polar axis at ![]() units to the left of the pole:
units to the left of the pole:
![]()
2. Directrix perpendicular to the polar axis at ![]() units to the right of the pole:
units to the right of the pole:
![]()
3. Directrix parallel to the polar axis at ![]() units above the pole:
units above the pole:
![]()
4. Directrix parallel to the polar axis at ![]() units below the pole:
units below the pole:
![]()
Please note:
-For ![]() , the conic is a parabola, the axis of symmetry is perpendicular to the
, the conic is a parabola, the axis of symmetry is perpendicular to the ![]()
-For ![]() , the conic is an ellipse. The major axis is perpendicular to the
, the conic is an ellipse. The major axis is perpendicular to the ![]()
-For ![]() , the conic is a hyperbola. The transverse axis is perpendicular to the
, the conic is a hyperbola. The transverse axis is perpendicular to the ![]()
Converting from polar to rectangular and vice-versa
We use the following relationships:
![]()
![]()
![]()
And of course:
![]()


Be the first to comment