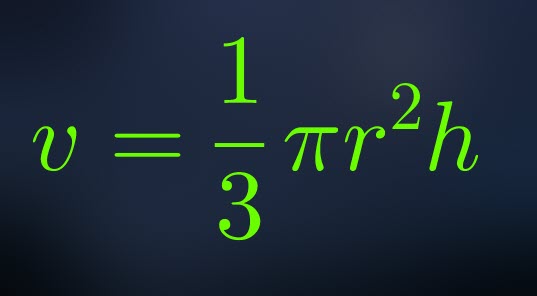
Implicit differentiation

Sometimes we are presented with equations in two variables, $x$ and $y$ that may have multiple solutions for $x$ in terms of $y$ or for $y$ in terms of $x$ .
The solutions found will be implicitly defined by the given equation.

For parametric functions, we use the following rule:

$\frac{dy}{dx}=\frac{dy/du}{dx/du}$

Problem 1
Given:
$x^{2}+y^{2}=1$
Find $y'$ or $\frac{dy}{dx}$

Solution:

$2x+2y \frac{dy}{dx}=0$
$2y \frac{dy}{dx}=-2x$
$\frac{dy}{dx}=-\frac{2x}{2y}$

Finally :
$\frac{dy}{dx}=-\frac{x}{y}$
We know that the given equation is a circle.
$\frac{dy}{dx}$ is simply the slope of the tangent of the circle at any point of coordinates $(x,y)$

Problem 2:
Given:
$xy+x-2y-1=0$
Find $y'$ or $\frac{dy}{dx}$

Solution:
$\frac{d(xy)}{dx}+\frac{dx}{dx}-\frac{d(2y)}{dx}-\frac{d(1)}{dx}=\frac{d(0)}{dx}$
$x\frac{dy}{dx}+y\frac{dx}{dx}+\frac{dx}{dx}-2\frac{dy}{dx}-\frac{d(1)}{dx}=\frac{d(0)}{dx}$
$x\frac{dy}{dx}+y+1-2\frac{dy}{dx}-0=0$
$(x-2)\frac{dy}{dx}+y+1=-(y+1)$
$\frac{dy}{dx}=-\frac{y+1}{x-2}=\frac{y+1}{2-x}$

Finally :
$\frac{dy}{dx}=-\frac{y+1}{x-2}=\frac{y+1}{2-x}$

Problem 3:

A sphere has a radius $R$ at time $t_{0}$ . What will be the value of that radius $R$ when the rate of increase of the volume $V$ is twice the rate of increase of the radius $R$ .

Find the corresponding value of the Volume $V$ .

Solution

The volume of a sphere is given by the formula:

$V=\frac{4}{3}\pi R^{3}$

$\frac{dV}{dt}=\frac{4}{3}\pi \cdot 3R^{2} \frac{dR}{dt}$

But: At the time when the rate of increase of $V$ is twice the one of $R$ , we can write:

$\frac{dV}{dt}=2 \frac{dR}{dt}$

$\frac{dV}{dt}=\frac{4}{3}\pi \cdot 3R^{2} \frac{dR}{dt} \Rightarrow 2\frac{dR}{dt}=\frac{4}{3}\pi \cdot 3R^{2} \frac{dR}{dt}$

We get:

$2=4 \pi R^{2} \Rightarrow R=\sqrt{\frac{2}{4 \pi}}$

$R=\sqrt{\frac{1}{2 \pi}}$

The volume $V$

$V=\frac{4}{3}\pi R^{3}$

$V=\frac{4}{3}\pi \left (\sqrt{\frac{1}{2 \pi}} \right )^{3}$

$V=\frac{4}{3}\pi \cdot \frac{1}{2 \pi} \sqrt{\frac{1}{2 \pi}}$

$V=\frac{2}{3} \sqrt{\frac{1}{2 \pi}}$

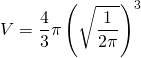
Finally:

$R=\sqrt{\frac{3}{4 \pi}}$

$V=\frac{2}{3} \sqrt{\frac{1}{2 \pi}}$

Problem 4:

Find the equation of the tangent and the normal to the curve:

$\begin{cases}x=a \cos^{4} \theta\\ y=a \sin^{4} \theta\end{cases}$

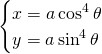
At the point $\theta=\frac{\pi}{4}$

Solution

We can find the $\frac{dy}{dx}$

$\frac{dy}{d \theta}=4a\sin^{3}\theta \cdot \cos \theta$

$\frac{dx}{d \theta}=-4a\cos^{3}\theta \cdot \sin \theta$

$\frac{dy}{dx}=\frac{4a\sin^{3}\theta \cdot \cos \theta}{-4a\cos^{3}\theta \cdot \sin \theta}$

$\frac{dy}{dx}=-\tan^{2} \theta$

At point $\theta=\frac{\pi}{4}$ :

$\frac{dy}{dx}=-\tan^{2} \frac{\pi}{4}=-1$

This is the slope of the tangent. It is clear that the slope of the normal is 1.

$y=a\sin^{4}\theta=a\sin^{4}\frac{\pi}{4}=\frac{1}{4}a=\frac{a}{4}$

$y=a\cos^{4}\theta=a\cos^{4}\frac{\pi}{4}=\frac{1}{4}a=\frac{a}{4}$

For the tangent, we know that:

$y-y_{0}=m(x-x_{0})$

$y-\frac{a}{4}=-1(x-\frac{a}{4})$

$y=-x+\frac{a}{4}+\frac{a}{4}$

$y=-x+\frac{a}{2}$

$x+y=\frac{a}{2}$

Equation of the tangent:

$2x+2y-a=0$

For the nomal we use the same method but different slope:

$y-\frac{a}{4}=1(x-\frac{a}{4})$

$y=x-\frac{a}{4}+\frac{a}{4}$

$y=x$

$x-y=0$

Equation of the normal:

$x-y=0$

Problem 5:

Water is being poured, at a rate of $10 ft^{3}/min$ into a leaking cylindrical cone shaped container with the top having 8 feet as diameter and which is 16 feet deep.
When the water is 12 feet deep, it was measured to be rising at a rate of $4 in/min$ .
How fast is the water leaking?

Solution

The ratio of cone height over radius is : $\frac{16}{4}$ . The diameter is 8 feet.

We can then write:

$\frac{h}{r}=4 \Rightarrow r=\frac{h}{4}$

Where $h$ is the height and $r$ is the radius.

Let $\frac{dv}{dt}$ be the rate of volume change at time $t$ .

$\frac{dL}{dt}$ be the leaking rate at time $t$ .

$\frac{df}{dt}$ be the filling rate at time $t$ . It is 10 ft^{3}/min at any given time.

$\frac{dh}{dt}$ is the rate of change of the height at any time

$\frac{dv}{dt}=\frac{df}{dt}-\frac{dL}{dt}$

The volume of the cone:
$v=\frac{1}{3} \pi r^{2} h$

But: $r=\frac{h}{4}$

$v=\frac{1}{3} \pi \frac{h^{2}}{16}h$

$v=\frac{1}{48} \pi h^{3}$

Taking the derivative of v with $h$ as variable:

$\frac{dv}{dt}=\frac{1}{48} \pi \cdot 3 h^{2}\frac{dh}{dt}$

$\frac{dv}{dt}=\frac{1}{16} \pi h^{2}\frac{dh}{dt}$

$\frac{dh}{dt}=4 in/min=\frac{1}{3}$ ft/min and $h=12$

$\frac{dv}{dt}=\frac{1}{16} \pi 12^{2}\frac{1}{3}$

$\frac{dv}{dt}=\frac{144}{48} \pi=3 \pi$

$3 \pi=10-\frac{dL}{dt}$

$\frac{dL}{dt}=10- 3 \pi$

Finally:

The leaking rate is $(10- 3 \pi)\; ft^{3}/min$

Problem 6:

Find the minimum distance from the point $(4,2)$ to the parabola $y^{2}=8x$

What is the equation of the tangent of the parabola at the point of the minimum distance to $(4,2)$

Solution

For each point we use the following coordinates:

$P(x, \sqrt{8x})$

The distance from any point:

$D^{2}=(x-x_{0})^{2}+(y-y_{0})^{2}$

$D^{2}=(x-4)^{2}+(\sqrt{8x}-2)^{2}$

$D^{2}=x^{2}-8x+16+8x-4 \sqrt{8x}+4$

$D^{2}=x^{2}-4 \sqrt{8x}+20$

The Distance:

$D=\sqrt{x^{2}-4 \sqrt{8x}+20}$

$\frac{dD}{dx}=\left(\sqrt{x^{2}-4 \sqrt{8x}+20} \right)'$

$\frac{dD}{dx}=\frac{1}{2}(x^{2}-4 \sqrt{8x}+20)^{-\frac{1}{2}}(x^{2}-4 \sqrt{8x}+20)'$

$\frac{dD}{dx}=\frac{2x-\frac{4}{2}(8x)^{-\frac{1}{2}}\cdot 8}{2\sqrt{x^{2}-4 \sqrt{8x}+20}}$

$\frac{dD}{dx}=\frac{2x\sqrt{8x}-16}{2\sqrt{8x}\sqrt{x^{2}-4 \sqrt{8x}+20}}$

We can see that the equation of the distance opens up. So the first derivative test is a minimum.

We just need the numerator to be $0$

$2x\sqrt{8x}-16=0$

$x\sqrt{8x}=8$

Let’s square both sides:
$x^{2}\cdot 8x=8^{2}$

$x^{3}=8$

$x=2$

When $x=2$ we can see that $y=\sqrt{8x}=\sqrt{16}=4$

Back to the distance to plug in $x$ and $y$ values:

$D=\sqrt{x^{2}-4 \sqrt{8x}+20}$

$D_{min}=\sqrt{2^{2}-4 \sqrt{16}+20}=\sqrt{24-16}=\sqrt{8}$

For the tangent:

$y^{2}=8x$

$2y\frac{dy}{dx}-8\frac{dx}{dx}=0$

$2y\frac{dy}{dx}=8$

$\frac{dy}{dx}=\frac{8}{2y}$

For our point $y=4$

The slope of the tangent is $m=\frac{8}{2 \times 4}$

$m=1$

The equation:

$y-y_{0}=m(x-x_{0})$

$y-4=1(x-2)$

$y-4=x-2$

$y=x-2+4$

$y=x+2$

Finally

$D_{min}=2 \sqrt{2}$

The tangent $y=x+2$

Post Views: 205

Implicit differentiation

Implicit differentiation

$\frac{dy}{dx}=\frac{dy/du}{dx/du}$

Be the first to comment

Leave a Reply Cancel reply