Introduction aux sections coniques
Les sections coniques peuvent être engendrées lorsqu’une ligne oblique tourne autour d’une ligne verticale en l’intersectant. On obtient deux cônes joints à cette intersection et s’étend indéfiniment vers le haut ou vers le bas.
Quand un plan coupe ce double cône, nous obtenons une section conique au niveau de l’intersection.
La position du plan définit le type de la section conique.
La section conique peut être: une parabole, ellipse, hyperbole, cercle, etc…
Le resumé qui suit nous permettra de résoudre les problèmes liés aux sections coniques.
La Parabole:
Une parabole est le lieu géométrique de tous les points situés à égale distance d’une droite fixe ![]() appelée directrice et d’un point fixe
appelée directrice et d’un point fixe ![]() appelé foyer.
appelé foyer.
Le point ![]() est le
est le ![]()
La ligne ![]() est la
est la ![]() .
.
![]()
La ligne qui passe par ![]() et perpendiculaire à la directrice
et perpendiculaire à la directrice ![]() est L’AXE DE SYMETRIE.
est L’AXE DE SYMETRIE.
Le point d’intersection de la parabole avec son axe de symétrie est le SOMMET que l’on note ![]() .
.
Si le sommet se trouve au point ![]() , avec le FOYER au point
, avec le FOYER au point ![]() avec
avec ![]() , par définition la DIRECTRICE sera la ligne
, par définition la DIRECTRICE sera la ligne ![]()
Cette définition avec la formule de distance:
![]()
Ce qui donne:
L’Equation de la parabole:
![]()
Le LATUS RECTUM ici est la longueur ![]() et est défini comme la ligne du segment joignant
et est défini comme la ligne du segment joignant ![]() and
and ![]()
Nous obtenons les cas suivants: Pour le SOMMET (h,k):
-Pour le sommet ![]() , nous avons le foyer
, nous avons le foyer ![]() , la DIRECTRICE sera la droite
, la DIRECTRICE sera la droite ![]() et l’équation est
et l’équation est ![]() . L’axe de symétrie est parallèle à l’axe des
. L’axe de symétrie est parallèle à l’axe des ![]() , s’ouvre vers la droite.
, s’ouvre vers la droite.
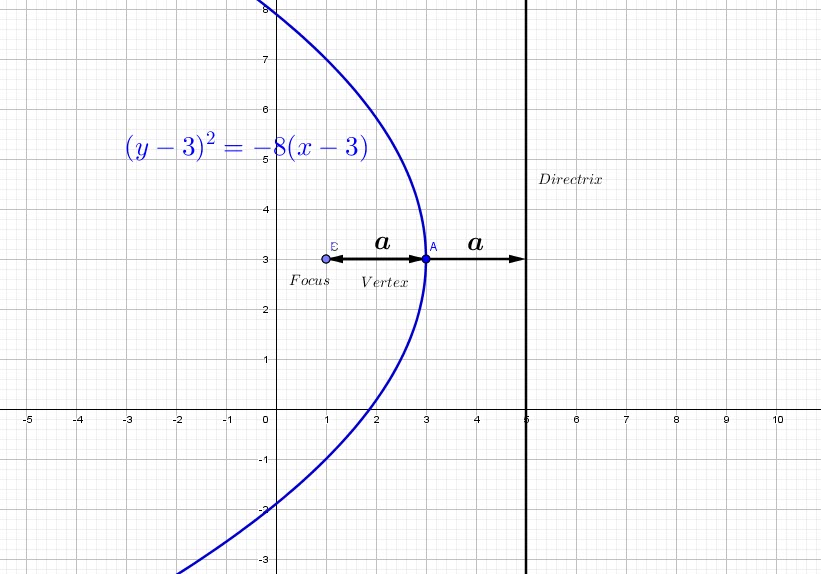
-Pour un sommet ![]() nous avons le foyer au point
nous avons le foyer au point ![]() , la DIRECTRICE sera la droite
, la DIRECTRICE sera la droite ![]() et l’Equation est
et l’Equation est ![]() avec un axe de symétrie parallele aux
avec un axe de symétrie parallele aux ![]() , ouverte à gauche.
, ouverte à gauche.
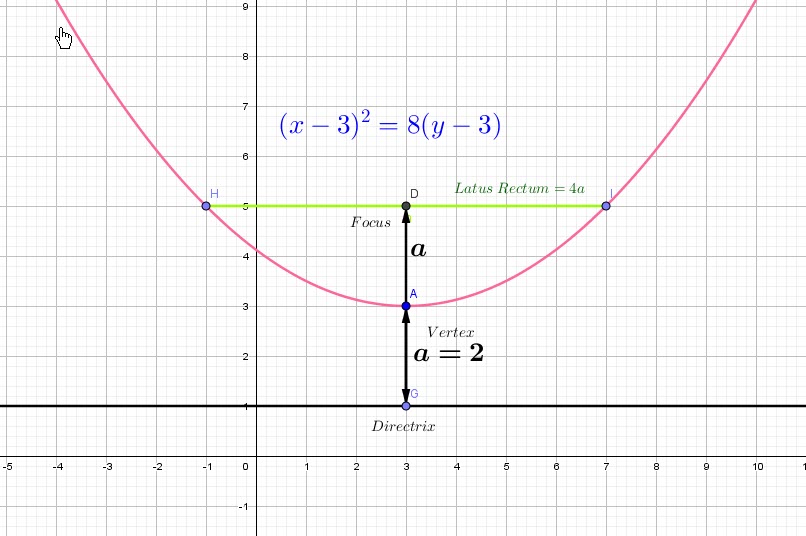
-Pour un sommet ![]() nous avons un foyer au point
nous avons un foyer au point ![]() , la DIRECTRICE sera la droite
, la DIRECTRICE sera la droite ![]() et l’Equation est
et l’Equation est ![]() avec un axe de symétrie parallele aux
avec un axe de symétrie parallele aux ![]() , ouverte vers le haut.
, ouverte vers le haut.
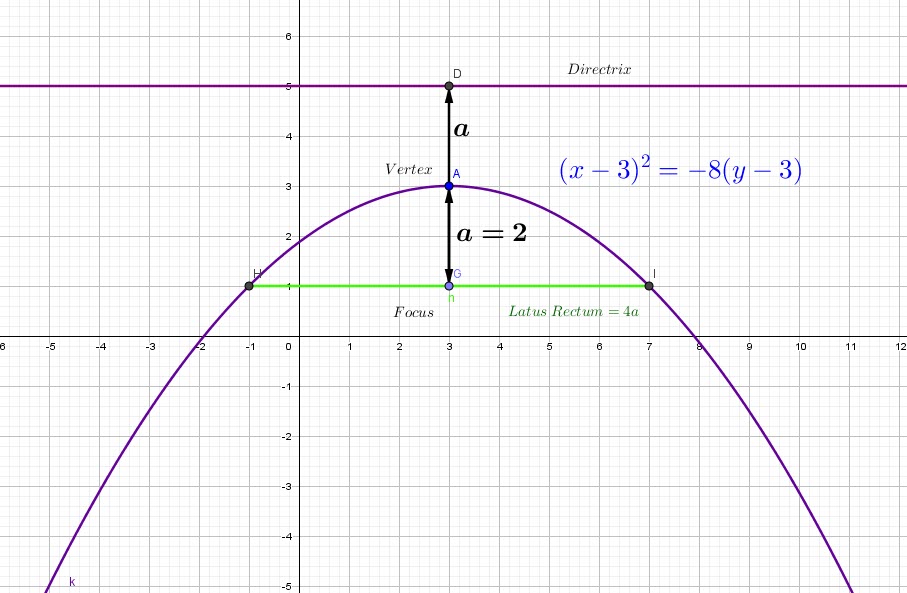
-Pour un sommet ![]() nous avons un foyer au point
nous avons un foyer au point ![]() , la DIRECTRICE sera la droite
, la DIRECTRICE sera la droite ![]() et l’Equation est
et l’Equation est ![]() avec un axe de symétrie parallele aux
avec un axe de symétrie parallele aux ![]() , ouverte vers le bas.
, ouverte vers le bas.
Nous avons les cas qui suivent: Pour un SOMMET AU (0,0):
-Avec un foyer sommet au ![]() nous avons le foyer
nous avons le foyer ![]() , la DIRECTRICE sera la droite
, la DIRECTRICE sera la droite ![]() et l’équation est
et l’équation est ![]() , l’axe de symétrie est parallèle à l’axe des
, l’axe de symétrie est parallèle à l’axe des ![]() , s’ouvrant vers la droite.
, s’ouvrant vers la droite.
-Avec un foyer sommet au ![]() , un foyer
, un foyer ![]() , la DIRECTRICE sera la droite
, la DIRECTRICE sera la droite ![]() et l’équation est
et l’équation est ![]() , l’axe de symétrie est parallèle à l’axe des
, l’axe de symétrie est parallèle à l’axe des ![]() , s’ouvrant vers la gauche.
, s’ouvrant vers la gauche.
-Avec un foyer sommet au ![]() , un foyer
, un foyer ![]() , la DIRECTRICE sera la droite
, la DIRECTRICE sera la droite ![]() et l’équation est
et l’équation est ![]() , l’axe de symétrie est parallèle à l’axe des
, l’axe de symétrie est parallèle à l’axe des ![]() , s’ouvrant vers le haut.
, s’ouvrant vers le haut.
-Avec un foyer sommet au ![]() , un foyer
, un foyer ![]() , la DIRECTRICE sera la droite
, la DIRECTRICE sera la droite ![]() et l’équation est
et l’équation est ![]() , l’axe de symétrie est parallèle à l’axe des
, l’axe de symétrie est parallèle à l’axe des ![]() , s’ouvrant vers le bas.
, s’ouvrant vers le bas.
L’Hyperbole:
Une hyperbole est le lieu géométrique de tous les points dont la différence des distances à deux points fixes appelés FOYERS est constante. Cette constante est égale à la distance entre les deux sommets de l’hyperbole. Le point milieu du segment joignant les deux sommets est le centre de l’hyperbole.
la droite passant par les deux foyers est L’AXE TRANSVERSAL.
Le ![]() de l’hyperbole est le point milieu du segment joignat les deux FOYERS.
de l’hyperbole est le point milieu du segment joignat les deux FOYERS.
La perpendiculaire à l’axe transversal passant par le centre s’appelle l’AXE CONJUGUÉ.
Les deux courbes représentant l’hyperbole sont les ![]()
Les points d’intersection de l’hyperbole et de l’axe transversal sont les ![]() de l’hyperbole.
de l’hyperbole.
Si ![]() ,
, ![]() avec
avec ![]() la distance entre le foyer et le centre.
la distance entre le foyer et le centre.
Pour tout point ![]() , nous avons:
, nous avons:
![]()
Utilisant la formule de distance:
Dans cette Equation ![]()
![]()
![]()
On élève les deux membres au carré:
![]()
On simplifie:
![]()
Simplifiant par 4:
![]()
![]()
On élève les deux membres au carré encore:
![]()
![]()
![]()
![]()
![]()
Let: ![]()
Nous avons:
![]()
En divisant les deux membres par ![]()
Nous avons la formule de l’hyperbole:
![]()
Ici l’axe transversal ![]()
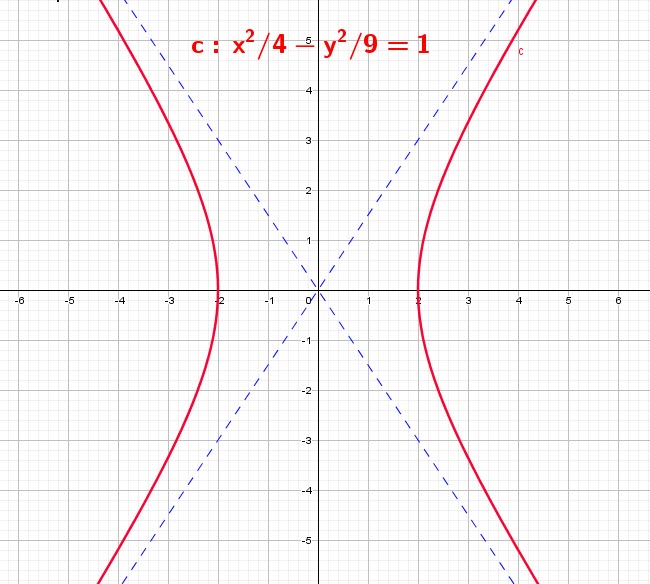
Asymptotes:
Nous apprendrons les calculs des limites dans d’autres chapitres.
Cependant si nous prenons:
![]()
Lorsque ![]() tend vers l’infini (à gauche ou à droite),la quantité
tend vers l’infini (à gauche ou à droite),la quantité ![]() tend vers
tend vers ![]()
Nous avons:
![]() and
and ![]()
Il y a deux asymptotes obliques:
![]() and
and ![]()
Pour une hyperbole de centre ![]() ; L’axe transversal sur l’axe des
; L’axe transversal sur l’axe des ![]()
Les foyers sont ![]() et
et ![]() ,
,
et les sommets sont ![]() et
et ![]()
![]()
Asymptotes:
Nous apprendrons les calculs des limites dans d’autres chapitres.
Cependant si nous prenons:
![]()
Lorsque ![]() tend vers l’infini (à gauche ou à droite),la quantité
tend vers l’infini (à gauche ou à droite),la quantité ![]() tend vers
tend vers ![]()
Nous avons:
![]() and
and ![]()
Il y a deux asymptotes obliques:
![]()
and
![]()
Equations de l’hyperbole:
L’axe transversal est parallèle aux ![]()
Centre ![]()
Foyers: ![]()
Sommets: ![]()
Equation:
![]()
![]()
Asymptotes:
![]()
L’axe transversal est parallèle aux ![]()
Centre ![]()
Foyers: ![]()
Sommet: ![]()
Equation:
![]()
![]()
Asymptotes:
![]()
ELLIPSE:
Une ellipse est le lieu géométrique de tous les points dont la somme des distances à deux points fixes appelés FOYERS est constante.
La droite contenant les deux foyers est L’AXE MAJEUR.
La perpendiculaire de l’axe majeur passant par le centre is l’AXE MINEUR.
Les points d’intersection de l’ellipse avec l’axe majeur sont les SOMMETS de l’ellipse.
Si ![]() et
et ![]() ,
, ![]() est la distance fixe: Point
est la distance fixe: Point ![]()
En utilisant les techniques similaires à celles de l’hyperbole on obtient:
![]()
![]() where
where ![]()
Ici l’axe majeur se trouve sur l’axe des ![]()
Pour l’Ellipse de centre ![]() ; TL’axe majeur se trouve sur l’axe des
; TL’axe majeur se trouve sur l’axe des ![]()
Les foyerst ![]() et
et ![]() ,
,
Et les sommets ![]() et
et ![]()
![]() où
où ![]()
![]()
Equations d’Ellipse:
L’axe majeur est parallèle à l’axe des ![]()
Centre ![]()
Foyers: ![]()
Sommets: ![]()
Equation:
![]()
![]()
L’axe majeur est parallèle à l’axe des ![]()
Centre ![]()
Foyers: ![]()
Sommets: ![]()
Equation:
![]()
![]()
Les Cercles
Un cercle esl l’ensemble des points dans le plan qui sont équidistants d’un point dans le plan, LE CENTRE
Cette distance est le ![]() .
.
Pour un cercle de ![]() .
.
Pour un point ![]()
Le rayon ![]() se trouve en utilisant la formule de distance;
se trouve en utilisant la formule de distance;
![]()
On élève les deux membres au carré:
![]()
L’Equation du cercle de centre ![]()
![]()
La tangente est perpendiculaire au rayon au point de tangence.
Pour plus détails, voir notre cours sur les cercles.
Equation générale des coniques
S’il n’y a pas un cas de dégeneration, on peut identifier les coniques comme suit:
![]() et
et ![]() ne peuvent pas avoir une valeur
ne peuvent pas avoir une valeur ![]() , tous les deux.
, tous les deux.
Lorsque ![]() , nous avons une PARABOLE
, nous avons une PARABOLE
Lorsque ![]() nous avons une ELLIPSE (or CERCLE)
nous avons une ELLIPSE (or CERCLE)
Lorsque ![]() , nous avons une HYPERBOLE
, nous avons une HYPERBOLE
On peut aussi utiliser:
![]()
Quand ![]() , nous avons une PARABOLE
, nous avons une PARABOLE
Quand ![]() nous avons une ELLIPSE (or CERCLE)
nous avons une ELLIPSE (or CERCLE)
Quand ![]() , on a une HYPERBOLE
, on a une HYPERBOLE
Coniques en Equations polaires
Pour une section conique, on appelle la droite ![]() la directrice,
la directrice, ![]() un foyer.
un foyer.
Nous allons introduire ![]() comme un numbre fixe positif, l’EXCENTRICITE
comme un numbre fixe positif, l’EXCENTRICITE
Les coniques peuvent se definir comme l’ensemble des points ![]() dont le rapport des distances
dont le rapport des distances ![]() sur
sur ![]() est
est ![]() .
.
– Pour une parabole ![]()
-Pour l’Ellipse nous avons ![]()
-Pour l’hyperbole ![]()
Si ![]() est la distance du centre au foyer et
est la distance du centre au foyer et ![]() est la distance du centre au sommet pour l’ellipse ou la parabole.
est la distance du centre au sommet pour l’ellipse ou la parabole.
Tout pointt ![]() peut avoir les coordonnées polaires
peut avoir les coordonnées polaires ![]()
![]()
En abaissant une perpendiculaire de ![]() à l’axe polaire avec le point
à l’axe polaire avec le point ![]() comme intersection, on a:
comme intersection, on a:
![]()
Mais on peut voirt ![]()
On remplace
![]()
![]()
En tirant ![]() nous avons:
nous avons:
L’Equation polaire de la section conique:
Avec ![]() comme excentricité de la section conique.
comme excentricité de la section conique.
Si la ![]() est perpendiculaire à l’axe polaire à une distance
est perpendiculaire à l’axe polaire à une distance ![]() à la droite du pôle:
à la droite du pôle:
Nous avons:
SOMMAIRE
1. Directrice perpendiculaire à l’axe polaire à ![]() unités à la gauche du pôle:
unités à la gauche du pôle:
![]()
2. Directrice perpendiculaire à l’axe polaire à ![]() unités à la droite du pôle:
unités à la droite du pôle:
![]()
3.Directrice parallèle à l’axe polaire à ![]() unités au dessus du pôle:
unités au dessus du pôle:
![]()
4. .Directrice parallèle à l’axe polaire à ![]() unités en bas du pôle:
unités en bas du pôle:
![]()
A noter:
-Pour ![]() , on a une parabole, l’axe de symétrie est perpendiculaire à la
, on a une parabole, l’axe de symétrie est perpendiculaire à la ![]()
-Pour ![]() , on a une ellipse. L’axe majeur est perpendiculaire à la
, on a une ellipse. L’axe majeur est perpendiculaire à la ![]()
-Pour ![]() , la section conique est une hyperbole. L’axe transversal est perpendiculaire à la
, la section conique est une hyperbole. L’axe transversal est perpendiculaire à la ![]()
Conversion des coordonnées polaires en coordonnées rectangulaires et vice-versa
On utilise la méthode suivante:
![]()
![]()
![]()
Et bien sûr:
![]()


Be the first to comment