
Fonctions hyperboliques
Nous avons déjà utilisé les fonctions hyperboliques dans certains de nos passages.
Ce qui suit n’est qu’un sommaire qui pourra nous permettre d’utiliser ces fonctions dans des passages qui suivront.
Nous examinerons leurs définitions et nous utiliserons les similarités avec les fonctions trigonométriques pour voir la plupart des formules.
{aridatatables moduleId=”158″}
Fonction cosinus hyperbolique
Le ![]() que l’on note
que l’on note ![]() se définit comme suit:
se définit comme suit:
![]()
Cette simple formule sera utilisée pour définir d’autres fonctions hyperboliques.

La fonction sinus hyperbolique
Le ![]() noté
noté ![]() se définit comme suit:
se définit comme suit:
![]()

Cette simple formule sera utilisée pour définir d’autres fonctions hyperboliques.
Autres fonctions hyperboliques
Sans surprise nous pouvons écrire:
![]()
Nous trouvons
![]()
A noter que:
![]()
Si l’on note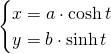
Quand ![]() change dans l’ensemble des réels, les points
change dans l’ensemble des réels, les points ![]() suivent une branche de l’hyperbole.
suivent une branche de l’hyperbole.
Trigonométrie hyperbolique
![]()
![]()
![]() Ceci montre que
Ceci montre que ![]()
On peut aussi montrer que:
![]()
Formules d’addition
Les relations ci-dessus montrent que:
![]()
![]()
![]()
![]()
Angle double:
![]()
![]()
Poue les tangentes:
![]()
![]()
![]()
Formules de Transformation
Les formules ci-dessus montrent que:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Si l’on pose ![]()
Nous obtenons de ce qui précéde:
![]()
![]()
![]()
Fonctions hyperboliques Inverses:
Soit ![]()
Nous pouvons écrire:
![]() with
with ![]()
Mais on sait que:
![]()
En remplaçant:
![]()
Prenant le ![]() des deux membres:
des deux membres:
![]()
Soit ![]()
On peut écrire:
![]() with
with ![]()
Mais on sait que:
![]()
En remplaçant:
![]()
Prenant le ![]() des deux membres:
des deux membres:
![]()
Problème 1:
Prouver l’égalité:
![]()
Solution
Pour résoudre ce problème nous utiliserons les formules qui suivent:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
On peut aussi prouver de la même manière que:
![]()
De retour à la formule:



Be the first to comment