
Intégrales indéfinies ou primitives
Ayant couvert les calculs des dérivées, on peut s’interesser à un autre sujet.
Connaissant la dérivée, on recherche la famille des fonctions qui diffèrent par des constantes et qui donnent cette dérivée après leur dérivation.
C’est le calcul de primitives qui devient intéressant dans notre cas de situation.
Une fonction ![]() est une primitive de la fonction
est une primitive de la fonction ![]() si
si ![]() pour tout
pour tout ![]() dans le domaine de
dans le domaine de ![]() .
.
Le seule problème est que la calcul de la dérivée d’une constante ![]() ,nous donne
,nous donne ![]() .
.
Voyons:
Si nous avons ![]()
Nous savons que ![]()
Mais c’est aussi: ![]() .
.
Quelle que soit la constante, la dérivée reste la même.
Et le théorème:
Théorème: Forme générale des primitives
Soit ![]() une primitive de
une primitive de ![]() sur un intervalle
sur un intervalle ![]() . Alors,
. Alors,
1. Pour toute constante ![]() , la fonction
, la fonction ![]() is aussi une primitive de
is aussi une primitive de ![]() sur
sur ![]() .
.
2. Si ![]() est une primitive de
est une primitive de ![]() sur
sur ![]() ,il existe une constante
,il existe une constante ![]() pour laquelle
pour laquelle ![]() sur
sur ![]() .
.
Ce qui donne la forme générale de la primitive de ![]() sur
sur ![]() comme
comme ![]() .
.
EXEMPLE:
Trouver la primitive de ![]()
Nous voyons que c’est ![]()
Intégrales indéfinies
Voici la notation utilisée pour les primitives:
![]()
![]() s’appelle
s’appelle ![]() et la variable
et la variable ![]() est la
est la ![]()
Formules Fundamentales
![]()
![]()
![]() with
with ![]() a constant
a constant
![]()
![]()
![]()
![]() with
with ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Problème 1:
Trouver: ![]()
Nous savons que ![]()
De ![]() nous voyons que
nous voyons que
![]()
Nous obtenons
(1) 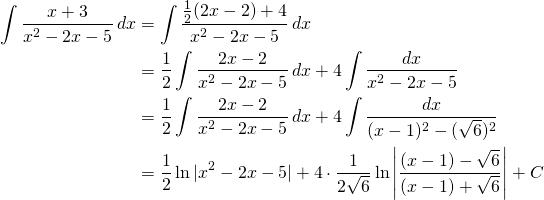
Finalement:
![]()
Problème 2:
Trouver: ![]()
Nous savons que ![]()
De ![]() nous voyons que
nous voyons que
![]()
Nous obtenons
(2) 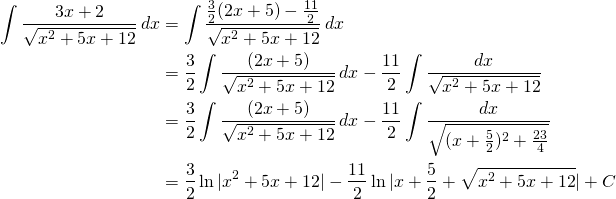
Finalement:
![]()


Be the first to comment