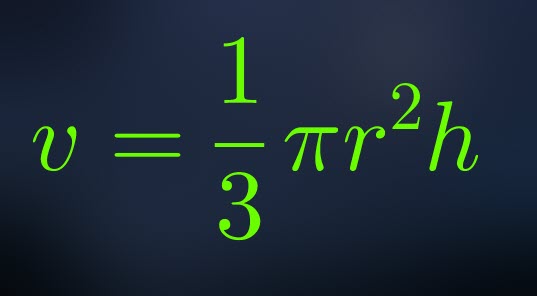
Dérivation implicite

Des fois on trouve des équations à deux variables, $x$ et $y$ pouvant avoir des solutions multiples pour $x$ en termes de $y$ ou pour $y$ en termes de $x$ .
Les solutions trouvées seront définie par l’équation donnée.

Nous utiliserons la règle suivante pour les fonctions paramétriques:

$\frac{dy}{dx}=\frac{dy/du}{dx/du}$

Problème 1
Etant donné que:
$x^{2}+y^{2}=1$
Trouver $y'$ ou $\frac{dy}{dx}$

Solution:

$2x+2y \frac{dy}{dx}=0$
$2y \frac{dy}{dx}=-2x$
$\frac{dy}{dx}=-\frac{2x}{2y}$

Finalement :
$\frac{dy}{dx}=-\frac{x}{y}$
C’est comme on le sait l’équation d’un cercle.
$\frac{dy}{dx}$ est simplement le coefficient directeur de la tengente au cercle en tout point de coordonnées $(x,y)$

Problème 2:
Etant donné que:
$xy+x-2y-1=0$
Trouver $y'$ or $\frac{dy}{dx}$

Solution:
$\frac{d(xy)}{dx}+\frac{dx}{dx}-\frac{d(2y)}{dx}-\frac{d(1)}{dx}=\frac{d(0)}{dx}$
$x\frac{dy}{dx}+y\frac{dx}{dx}+\frac{dx}{dx}-2\frac{dy}{dx}-\frac{d(1)}{dx}=\frac{d(0)}{dx}$
$x\frac{dy}{dx}+y+1-2\frac{dy}{dx}-0=0$
$(x-2)\frac{dy}{dx}+y+1=-(y+1)$
$\frac{dy}{dx}=-\frac{y+1}{x-2}=\frac{y+1}{2-x}$

Finalement :
$\frac{dy}{dx}=-\frac{y+1}{x-2}=\frac{y+1}{2-x}$

Problème 3:

Soit une sphère de rayon $R$ au temps $t_{0}$ . Quel sera la valeur de ce rayon $R$ quand le taux d’augmentation du volume $V$ est le double du taux d’augmentationdu rayon $R$ .

Trouver la valeur correspondante du volume $V$ .

Solution

Le volume de la sphère est donné par la formule:

$V=\frac{4}{3}\pi R^{3}$

$\frac{dV}{dt}=\frac{4}{3}\pi \cdot 3R^{2} \frac{dR}{dt}$

Mais: Au moment ou le taux d’augmentation de $V$ est le double de celui de $R$ , on peut écrire:

$\frac{dV}{dt}=2 \frac{dR}{dt}$

$\frac{dV}{dt}=\frac{4}{3}\pi \cdot 3R^{2} \frac{dR}{dt} \Rightarrow 2\frac{dR}{dt}=\frac{4}{3}\pi \cdot 3R^{2} \frac{dR}{dt}$

Nous aurons:

$2=4 \pi R^{2} \Rightarrow R=\sqrt{\frac{2}{4 \pi}}$

$R=\sqrt{\frac{1}{2 \pi}}$

Le volume $V$

$V=\frac{4}{3}\pi R^{3}$

$V=\frac{4}{3}\pi \left (\sqrt{\frac{1}{2 \pi}} \right )^{3}$

$V=\frac{4}{3}\pi \cdot \frac{1}{2 \pi} \sqrt{\frac{1}{2 \pi}}$

$V=\frac{2}{3} \sqrt{\frac{1}{2 \pi}}$

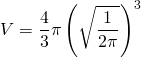
Finalement:

$R=\sqrt{\frac{3}{4 \pi}}$

$V=\frac{2}{3} \sqrt{\frac{1}{2 \pi}}$

Problème 4:

Trouver l’equation de la tangente et de la normale à la courbe:

$\begin{cases}x=a \cos^{4} \theta\\ y=a \sin^{4} \theta\end{cases}$

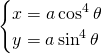
au point $\theta=\frac{\pi}{4}$

Solution

On peut trouver $\frac{dy}{dx}$

$\frac{dy}{d \theta}=4a\sin^{3}\theta \cdot \cos \theta$

$\frac{dx}{d \theta}=-4a\cos^{3}\theta \cdot \sin \theta$

$\frac{dy}{dx}=\frac{4a\sin^{3}\theta \cdot \cos \theta}{-4a\cos^{3}\theta \cdot \sin \theta}$

$\frac{dy}{dx}=-\tan^{2} \theta$

Au point $\theta=\frac{\pi}{4}$ :

$\frac{dy}{dx}=-\tan^{2} \frac{\pi}{4}=-1$

C’est le coefficient directeur de la tangente.Il s’en va de soit que le coeffient directeur de la normale est de 1.

$y=a\sin^{4}\theta=a\sin^{4}\frac{\pi}{4}=\frac{1}{4}a=\frac{a}{4}$

$y=a\cos^{4}\theta=a\cos^{4}\frac{\pi}{4}=\frac{1}{4}a=\frac{a}{4}$

Pour la tangente nous savons que:

$y-y_{0}=m(x-x_{0})$

$y-\frac{a}{4}=-1(x-\frac{a}{4})$

$y=-x+\frac{a}{4}+\frac{a}{4}$

$y=-x+\frac{a}{2}$

$x+y=\frac{a}{2}$

Equation de la tangente:

$2x+2y-a=0$

Pour la normale on procède de la même manière:

$y-\frac{a}{4}=1(x-\frac{a}{4})$

$y=x-\frac{a}{4}+\frac{a}{4}$

$y=x$

$x-y=0$

Equation de la normale:

$x-y=0$

Problem 5:

On verse da l’eau, à une vitesse de $10 ft^{3}/min$ dans une récipient de forme cône cylindrique qui coule avec un diamètre 8 ft en haut et une hauteur de 16 ft.
Quang l’eau aura une hauteru de 12 ft, le récipient se remplissait à une vitesse $4 in/min$ .
A quel débit l’eau coule?

Solution

Le rapport de la hauteur du cône sur son rayon est de : $\frac{16}{4}$ . Le diamètre étant de 8 feet.

Nous avons:

$\frac{h}{r}=4 \Rightarrow r=\frac{h}{4}$

Avec $h$ la hauteur et $r$ le rayon.

Soit $\frac{dv}{dt}$ le taux de variation du volume au temps $t$ .

$\frac{dL}{dt}$ le débit avec lequel l’eau sort du cône en coulant au temps $t$ .

$\frac{df}{dt}$ le débit avec lequel l’eau remplit le cône au temps $t$ .Il est de 10 f^{3}/min à tout moment.

$\frac{dh}{dt}$ est le taux de variation de la hateur à tout moment.

$\frac{dv}{dt}=\frac{df}{dt}-\frac{dL}{dt}$

Le volume du cône:
$v=\frac{1}{3} \pi r^{2} h$

Mais: $r=\frac{h}{4}$

$v=\frac{1}{3} \pi \frac{h^{2}}{16}h$

$v=\frac{1}{48} \pi h^{3}$

On prend la dérivée de v avec $h$ comme variable:

$\frac{dv}{dt}=\frac{1}{48} \pi \cdot 3 h^{2}\frac{dh}{dt}$

$\frac{dv}{dt}=\frac{1}{16} \pi h^{2}\frac{dh}{dt}$

$\frac{dh}{dt}=4 in/min=\frac{1}{3}$ ft/min and $h=12$

$\frac{dv}{dt}=\frac{1}{16} \pi 12^{2}\frac{1}{3}$

$\frac{dv}{dt}=\frac{144}{48} \pi=3 \pi$

$3 \pi=10-\frac{dL}{dt}$

$\frac{dL}{dt}=10- 3 \pi$

Finalement:

Le débit de fuite de l’eau $(10- 3 \pi)\; ft^{3}/min$

Problème 6:

Trouver la plus courte distance entre le point $(4,2)$ et la parabole $y^{2}=8x$

Quelle est l’équation de la tangente à la parabole au point où la distance de la parabole au point $(4,2)$ est la plus

courte

Solution

Pour tout point on peut utiliser les coordonnées suivantes:

$P(x, \sqrt{8x})$

La distance à tout point est de:

$D^{2}=(x-x_{0})^{2}+(y-y_{0})^{2}$

$D^{2}=(x-4)^{2}+(\sqrt{8x}-2)^{2}$

$D^{2}=x^{2}-8x+16+8x-4 \sqrt{8x}+4$

$D^{2}=x^{2}-4 \sqrt{8x}+20$

La distance:

$D=\sqrt{x^{2}-4 \sqrt{8x}+20}$

$\frac{dD}{dx}=\left(\sqrt{x^{2}-4 \sqrt{8x}+20} \right)'$

$\frac{dD}{dx}=\frac{1}{2}(x^{2}-4 \sqrt{8x}+20)^{-\frac{1}{2}}(x^{2}-4 \sqrt{8x}+20)'$

$\frac{dD}{dx}=\frac{2x-\frac{4}{2}(8x)^{-\frac{1}{2}}\cdot 8}{2\sqrt{x^{2}-4 \sqrt{8x}+20}}$

$\frac{dD}{dx}=\frac{2x\sqrt{8x}-16}{2\sqrt{8x}\sqrt{x^{2}-4 \sqrt{8x}+20}}$

Une quadratique ouverte vers le haut. La dérivée s’ennule au minimum.

Le numéteur s’ennule comme suit:

$2x\sqrt{8x}-16=0$

$x\sqrt{8x}=8$

Elevant les deux membres au carré:
$x^{2}\cdot 8x=8^{2}$

$x^{3}=8$

$x=2$

Quand $x=2$ won voit que $y=\sqrt{8x}=\sqrt{16}=4$

Retournant au calcul de distance, remplaçant $x$ et $y$ par leurs valeurs:

$D=\sqrt{x^{2}-4 \sqrt{8x}+20}$

$D_{min}=\sqrt{2^{2}-4 \sqrt{16}+20}=\sqrt{24-16}=\sqrt{8}$

Pour la tangente:

$y^{2}=8x$

$2y\frac{dy}{dx}-8\frac{dx}{dx}=0$

$2y\frac{dy}{dx}=8$

$\frac{dy}{dx}=\frac{8}{2y}$

Pour notre point $y=4$

Le coefficient directeur de la tangente $m=\frac{8}{2 \times 4}$

$m=1$

L’équation:

$y-y_{0}=m(x-x_{0})$

$y-4=1(x-2)$

$y-4=x-2$

$y=x-2+4$

$y=x+2$

Finalement

$D_{min}=2 \sqrt{2}$

La tangente est $y=x+2$

Post Views: 902

Dérivation implicite

Dérivation implicite

$\frac{dy}{dx}=\frac{dy/du}{dx/du}$

Be the first to comment

Leave a Reply Cancel reply