Promoting the study of Geometry

Joining forces with institut-delbol.com, mouctar.org is publishing the first challenge.

The callenge second part is now solved. No more answers will be accepted. There was no winner for this challenge.

PROBLEM 2: THE TRAPEZOID

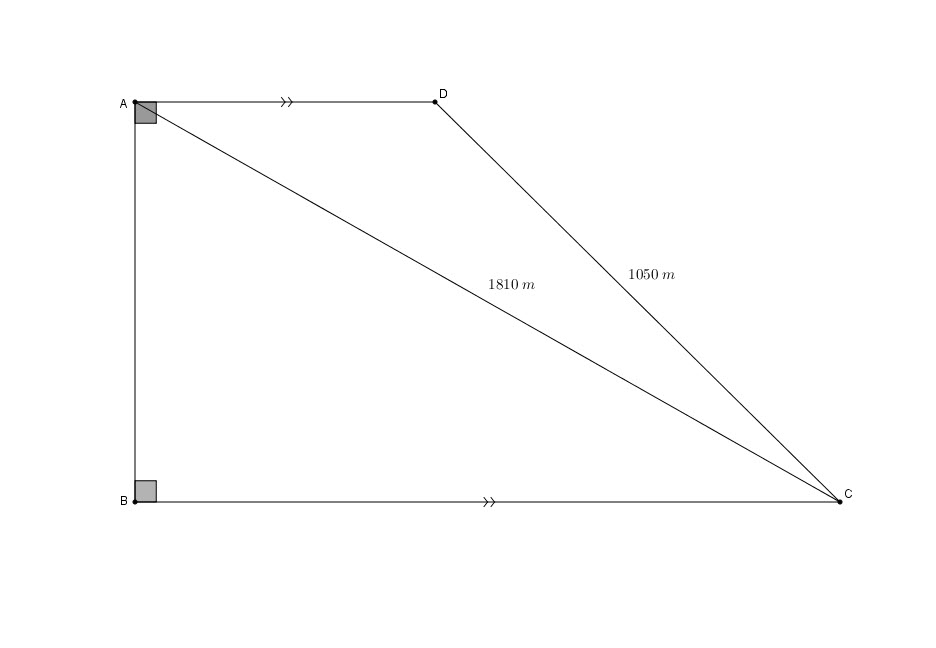
An agency is assigning the area bounded by figure $ABCD$ to a city population.

Each member will receive an equal area of a land plot.

Calculations have shown that out of the 5160 members of the population, 2000 will receive their plots from the area covered by triangle $ADC$

The remaining people will be assigned plots from $ABC$ , (See graph).

$DC=1050\;m$ and $AC=1810\:m$

1. Find the area of $ABCD$ $(30\; points)$

2. Verify the area of ADC using the Heron’s Formula $(10\; points)$

3. What is the area, in square meters, assigned to each person? $(10\; points)$

Click this link to read the pdf file

SOLUTION: METHOD BY TRIGONOMETRY

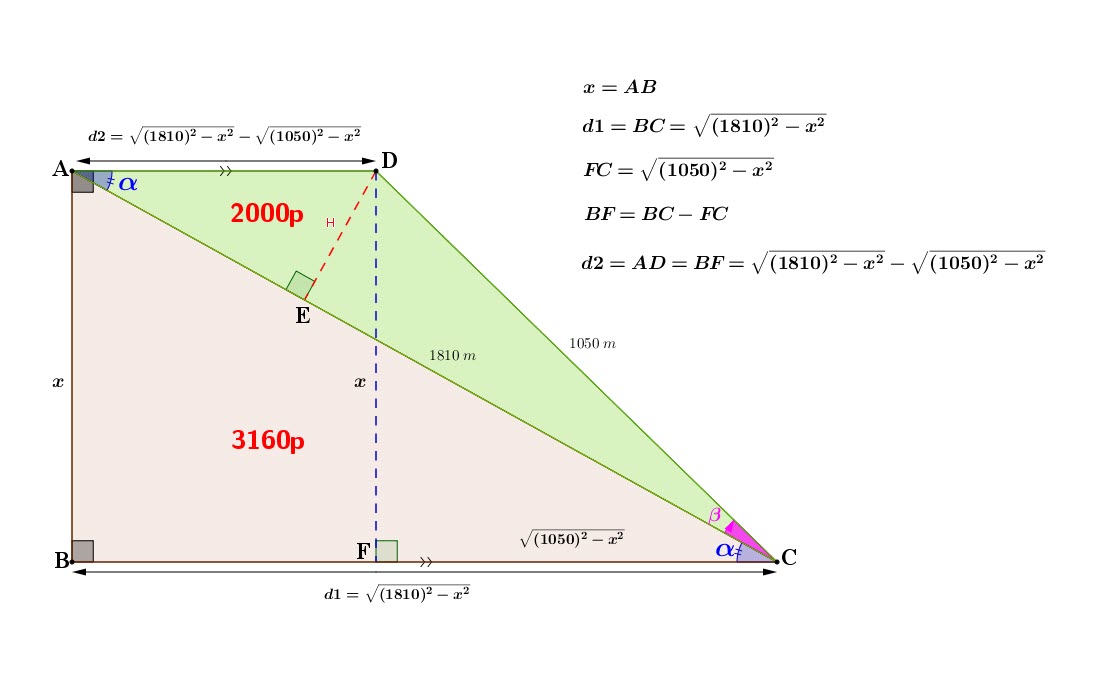
Let $AB=x$

$BC=d_{1}$

From the right triangle $\triangle ABC$ We have the hypothenuse $AC=1810$ .

We have:

$d_{1}=\sqrt{(1810)^{2}-x^{2}}$

We also have the right triangle $\triangle DFC$

$FC=\sqrt{(1050)^{2}-x^{2}}$

Another equality:

$AD=d_{2}=BF=BC-FC$

We can then say:

$d_{2}=\sqrt{(1810)^{2}-x^{2}}-\sqrt{(1050)^{2}-x^{2}}$

We can also see that :

$\angle BCA \cong \angle CAD$

$m\angle BCA=\alpha=m\angle CAD$

The area of $\triangle ABC$ contains 3160 plots of land:

$Area;\triangle ABC=3160p$

Also

$Area;\triangle ACD=2000p$

If we use areas by angle and adjacent sides we get:

For $\triangle ABC$ :

$\frac{1}{2}\cdot BC \cdot AC \cdot \sin {\alpha}=3160p \tag{1} \label{1}$

For $\triangle ACD$ :

$\frac{1}{2}\cdot AD \cdot AC \cdot \sin {\alpha}=2000p \tag{2} \label{2}$

Now let’s divide $(1)$ by $(2)$

$\displaystyle{\frac{\frac{1}{2}\cdot BC \cdot AC \cdot \sin {\alpha}}{\frac{1}{2}\cdot AD \cdot AC \cdot \sin {\alpha}}=\frac{3160p}{2000p}}$

Simplifying we get:

$\frac{BC}{AD}=\frac{3.16}{2}$

$\frac{BC}{AD}=1.58$

But $d_{1}=BC$ and $d_{2}=AD$

We get:

$\displaystyle{\frac{\sqrt{(1810)^{2}-x^{2}}}{\sqrt{(1810)^{2}-x^{2}}-\sqrt{(1050)^{2}-x^{2}}}=1.58}$

Multiplying both members by the denominator of the left side:

$\sqrt{(1810)^{2}-x^{2}}=1.58(\sqrt{(1810)^{2}-x^{2}}-\sqrt{(1050)^{2}-x^{2}})$

$\sqrt{(1810)^{2}-x^{2}}=1.58(\sqrt{(1810)^{2}-x^{2}})-1.58(\sqrt{(1050)^{2}-x^{2}})$

$(1.58-1)\sqrt{(1810)^{2}-x^{2}}=1.58\sqrt{(1050)^{2}-x^{2}}$

$0.58\sqrt{(1810)^{2}-x^{2}}=1.58\sqrt{(1050)^{2}-x^{2}}$

$\sqrt{(1810)^{2}-x^{2}}=\frac{1.58}{0.58}\sqrt{(1050)^{2}-x^{2}}$

$\sqrt{(1810)^{2}-x^{2}}=\frac{0.79}{0.29}\sqrt{(1050)^{2}-x^{2}}$

Let $k=\frac{0.79}{0.29}$

We get:

$\sqrt{(1810)^{2}-x^{2}}=k\sqrt{(1050)^{2}-x^{2}}$

Let’s square both sides:

$(1810)^{2}-x^{2}=k^{2}((1050)^{2}-x^{2})$

$(1810)^{2}-x^{2}=k^{2}(1050)^{2}-k^{2}x^{2}$

$(k^{2}-1)x^{2}=k^{2}\cdot (1050)^{2}-(1810)^{2}$

$\displaystyle{ x^{2}=\frac{k^{2}\cdot (1050)^{2}-(1810)^{2}}{k^{2}-1}}$

$\displaystyle{x=\sqrt{\frac{k^{2}\cdot (1050)^{2}-(1810)^{2}}{k^{2}-1}}}$

We plugin the values:

$\displaystyle{x=\sqrt{\frac{(\frac{0.79}{0.29})^{2}\cdot (1050)^{2}-(1810)^{2}}{(\frac{0.79}{0.29})^{2}-1}}}$

$x=874.0605963$

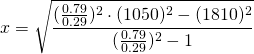
Rounded Value here:

$x=874\; m$

Finding angles $\alpha$ and $\beta$

$\sin \alpha=\frac{x}{1810}$

Yields

$\displaystyle{\sin \alpha=\frac{874.0605963}{1810} \Leftarrow \alpha=28^{\circ}.8753967}$

On the other hand, in $\triangle ADC$ :

$\displaystyle{\frac{\sin {(180^{\circ}-(\alpha+\beta))}}{1810}=\frac{\sin {\alpha}}{1050} \Rightarrow \frac{\sin {(\alpha+\beta)}}{1810}=\frac{\sin {\alpha}}{1050}}$

Which gives:

$\sin {(\alpha+\beta)}=\frac{1810}{1050}\sin {\alpha}$

$\displaystyle{\displaystyle{\sin {(\alpha+\beta)}=\frac{1810}{1050}\sin {28^{\circ}.8753967} \Leftarrow (\alpha+\beta)=56^{\circ}.35006873}}$

We then get

$\beta=56^{\circ}.35006873-28^{\circ}.8753967$

$\beta=27^{\circ}.47467203$

Areas:

Area $\triangle ABC=\frac{1}{2}\cdot x \cdot AC \cdot \cos {\alpha}$

Area $\triangle ABC=\frac{1}{2}\times 874.0605963\times 1810 \times \cos {28^{\circ}.8753967}$

Area $\triangle ABC=692678.2811$

Rounding:

Area $\triangle ABC=692678 \;m^{2}$

For $\triangle ADC$

Area $\triangle ADC=\frac{1}{2}\cdot 1050 \cdot 1810 \cdot \sin {\beta}$

Area $\triangle ADC=\frac{1}{2}\cdot 1050 \cdot 1810 \cdot \sin {27^{\circ}.47467203}$

Area $\triangle ADC=438403.9754$

ROUNDING

Area $\triangle ADC=438404\; m^{2}$

$TOTAL\; AREA:$

We add the two areas:

$AREA\; ABCD=692678+438404$

$AREA\; ABCD=1131082\;m^{2}$

$SIZE\; OF \;THE\; PLOT:\; 5160\; plots$

$AREA \;PLOT=\frac{1131082}{5160}$

$AREA \;PLOT=219\;m^{2}$

Using the heron Formula for Area ADC

Calculating $d_{2}$

$\displaystyle{\frac{\sin {\alpha}}{1050}=\frac{\sin {\beta}}{d_{2}} \Rightarrow d_{2}=1050 \cdot \frac{\sin {\beta}}{\sin {\alpha}}}$

$\displaystyle{d_{2}=1050 \cdot \frac{\sin {27^{\circ}.47467203}}{\sin {28^{\circ}.8753967}}}$

$d_{2}=1003.143208$

The sides are: $1050$ , $1810$ , $1003.143208$

Calculating $s$ :

$s=\frac{1050+1810+1003.143208}{2}$

$s=1931.571604$

$s-1050=1931.571604-1050=881.571604$

$s-1810=1931.571604-1810=121.571604$

$s-1003.143208=1931.571604-1003.143208=928.428396$

Area $\triangle ADC=\sqrt{1931.571604 \times 881.571604 \times 121.571604 \times 928.428396 }$

Area $\triangle ADC=438403.9751$

ROUNDING:

Area $\triangle ADC=438404\; m^{2}$

Post Views: 660

Challenge 1 Spring of 2017: Trapezoid Solution

Promoting the study of Geometry

PROBLEM 2: THE TRAPEZOID

SOLUTION: METHOD BY TRIGONOMETRY

Areas:

Using the heron Formula for Area ADC

Be the first to comment

Leave a Reply Cancel reply