Promotion de la Géometrie élémentaire

En accord avec l’ institut-delbol.com, mouctar.org punlie en cette fin Septembre 2018 la solution du problème sur les parcelles.

La deuxième partie du défi est ainsi résolue.Aucune réponse sur ce problème ne sera acceptée. Pas de gagnant cette fois..

PROBLEME 2: LE TRAPEZE

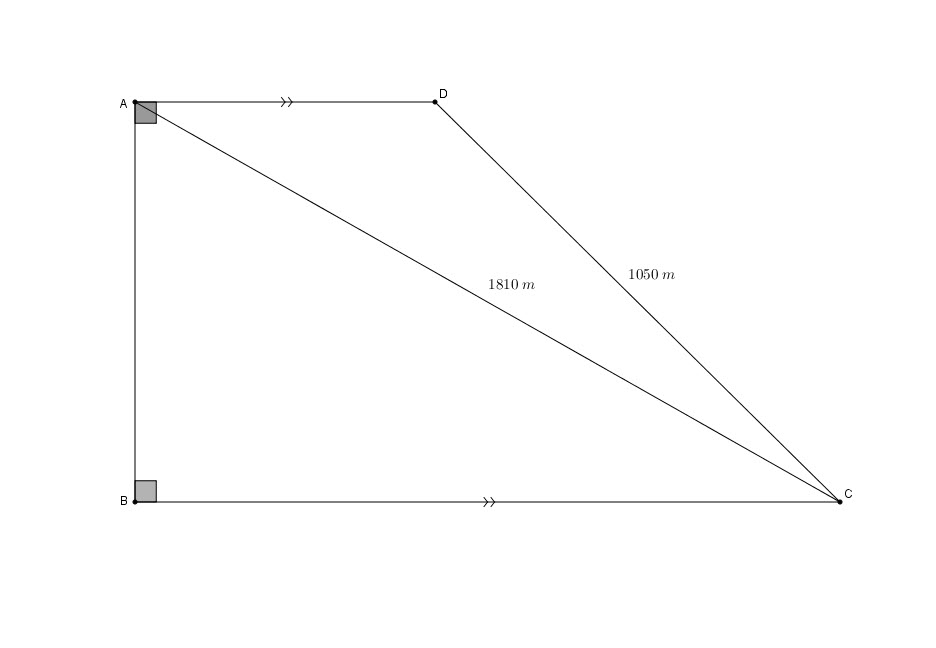
Un domaine a été mis en vente par l’autorité compétente.

Au total 5160 parcelles des superficies égales peuvent être assignées.

Les calculs montrent que 2000 parcelles peuvent être assignées au niveau de la zone couverte par le triangle $ADC$ .

Le reste des parcelles couvrent la zone du triangle $ABC$ (Voir figure).

$DC=1050\;m$ et $AC=1810\:m$ .

1.Trouvez la superficie totale de la zone $ABCD$ . (30 points)

2.Vérifier par la formule de Héron l’aire de la zone $ADC$ . (10 points)

3. Quelle sera la superficie de chaque parcelle? (10 points)

$N.B.\;Tous\; les \;calculs \;seront \;effectués\; avec \;une\; précision \;de \;5\; décimales$

Cliquer ici pour le fichier pdf

SOLUTION: Par méthode Algébrique

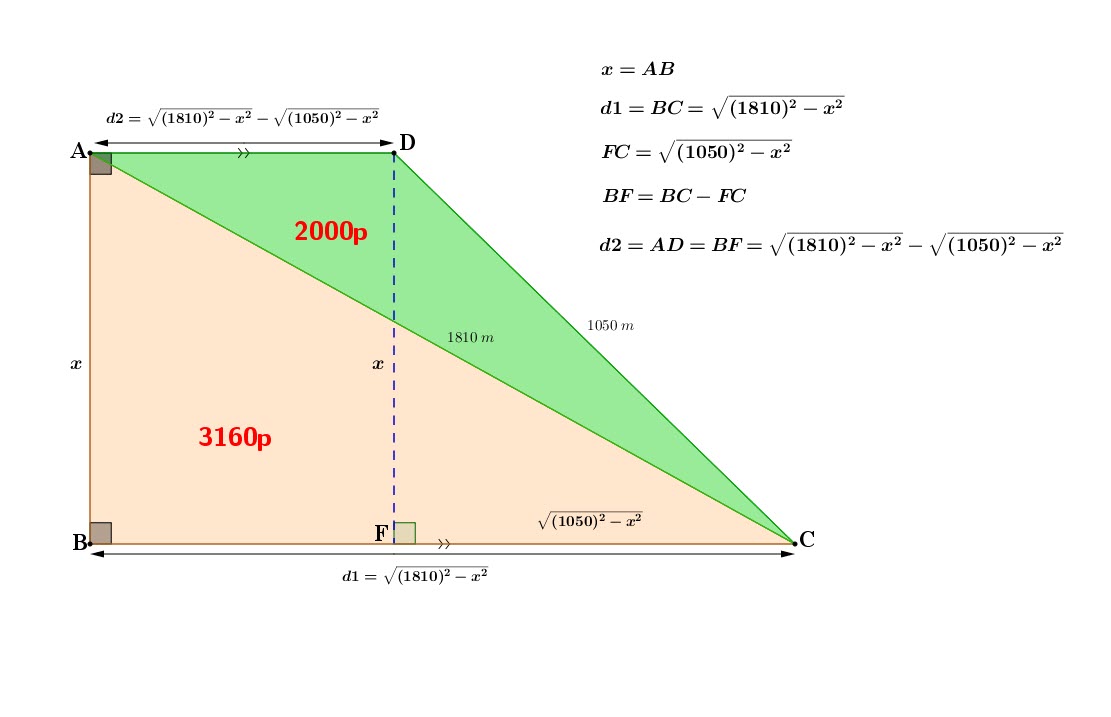
Soit $AB=x$

$BC=d_{1}$

Pour le triangle rectangle $\triangle ABC$ nous avons l’hypothenuse $AC=1810$ .

Nous avons:

$d_{1}=\sqrt{(1810)^{2}-x^{2}}$

Nous avons aussi le triangle rectangle $\triangle DFC$

$FC=\sqrt{(1050)^{2}-x^{2}}$

Une autre égalité:

$AD=d_{2}=BF=BC-FC$

Nous pouvons aussi écrire:

$d_{2}=\sqrt{(1810)^{2}-x^{2}}-\sqrt{(1050)^{2}-x^{2}}$

L’aire de la surface $\mathcal{A}\triangle ABC$ doit contenir 3160 parcelles sur 5160.

Pour $\triangle ABC$ :

$\mathcal{A} \triangle ABC$

L’aire de la surface $\mathcal{A}\triangle ABC=\frac{1}{2}\cdot x \cdot BC$

OU BIEN

$\mathcal{A}\triangle ABC=\frac{1}{2}\cdot x \cdot d_{1}$

$\mathcal{A}\triangle ABC=\frac{1}{2}x \sqrt{(1810)^{2}-x^{2}}$

Maintenant cherchons la surface totale:

$\mathcal{A}\;\square ABCD=\square ABFD+\triangle DFC$

L’aire de la surface $\mathcal{A}\;\square ABFD$ :

L’aire de la surface $\mathcal{A}\;\square ABFD=x\cdot d_{2}$

On remplace:

$\displaystyle{\mathcal{A}\;\square ABFD=x\cdot (\sqrt{(1810)^{2}-x^{2}}-\sqrt{(1050)^{2}-x^{2}})}$

$\displaystyle{\mathcal{A}\;\square ABFD=x\sqrt{(1810)^{2}-x^{2}}-x\sqrt{(1050)^{2}-x^{2}}}$

Pour le $\triangle DFC$ :

L’aire de la surface $\mathcal{A}\;\triangle DFC=\frac{1}{2}\cdot x \cdot FC$

OU BIEN

L’aire de la surface $\mathcal{A}\;\triangle DFC=\frac{1}{2}\cdot x \cdot d_{1}$

L’aire de la surface $\displaystyle{\mathcal{A}\;\triangle DFC=\frac{1}{2}\cdot x \cdot \sqrt{(1050)^{2}-x^{2}}}$

SURFACE TOTALE :

L’aire de la surface $\mathcal{A}\;\square ABCD=\square ABFD+\triangle DFC$

On remplace:

L’aire de la surface $\displaystyle{\mathcal{A}\;\square ABCD=x\sqrt{(1810)^{2}-x^{2}}-x\sqrt{(1050)^{2}-x^{2}}+\frac{1}{2}x \sqrt{(1050)^{2}-x^{2}}}$

L’aire de la surface $\mathcal{A}\;\square ABCD=x\sqrt{(1810)^{2}-x^{2}}-\frac{1}{2}x \sqrt{(1050)^{2}-x^{2}}$

Comparons les aires:

L’aire du $\triangle ABC=3160p$

L’aire du $\square ABCD=5160p$

Ce qui donne:

$\frac{Area\; \square ABCD}{Area \; \triangle ABC}=\frac{5160p}{3160p}$

Ou bien:

$\mathcal{A} \; \triangle ABC=\frac{3160p}{5160p}Area\; \square ABCD$

On simplifie:

$\mathcal{A} \; \triangle ABC=\frac{79}{129}Area\; \square ABCD$

En remplaçant:

$\displaystyle{\frac{1}{2} x \sqrt{(1810)^{2}-x^{2}}=\frac{79}{129}(x\sqrt{(1810)^{2}-x^{2}}-\frac{1}{2}x \sqrt{(1050)^{2}-x^{2}})}$

Nous pouvons écrire:

$\displaystyle{\frac{129}{158}x \sqrt{(1810)^{2}-x^{2}}=x\sqrt{(1810)^{2}-x^{2}}-\frac{1}{2}x \sqrt{(1050)^{2}-x^{2}}}$

Divisons les deux membres par $x$

$\frac{129}{158} \sqrt{(1810)^{2}-x^{2}}=\sqrt{(1810)^{2}-x^{2}}-\frac{1}{2} \sqrt{(1050)^{2}-x^{2}}$

On arrange:

$\frac{1}{2} \sqrt{(1050)^{2}-x^{2}}=(1-\frac{129}{158}) \sqrt{(1810)^{2}-x^{2}}$

$\frac{1}{2} \sqrt{(1050)^{2}-x^{2}}=\frac{29}{158} \sqrt{(1810)^{2}-x^{2}}$

Multiplions les deux membres par 2:

$\sqrt{(1050)^{2}-x^{2}}=\frac{29}{79} \sqrt{(1810)^{2}-x^{2}}$

Nous pouvons aussi écrire:

$\frac{0.79}{0.29}\sqrt{(1050)^{2}-x^{2}}=\sqrt{(1810)^{2}-x^{2}}$

Soit $k=\frac{0.79}{0.29}$

Nous avons:

$\sqrt{(1810)^{2}-x^{2}}=k\sqrt{(1050)^{2}-x^{2}}$

Elevons les 2 membres au carré:

$(1810)^{2}-x^{2}=k^{2}((1050)^{2}-x^{2})$

$(1810)^{2}-x^{2}=k^{2}(1050)^{2}-k^{2}x^{2}$

$(k^{2}-1)x^{2}=k^{2}\cdot (1050)^{2}-(1810)^{2}$

$\displaystyle{x^{2}=\frac{k^{2}\cdot (1050)^{2}-(1810)^{2}}{k^{2}-1}}$

$\displaystyle{x=\sqrt{\frac{k^{2}\cdot (1050)^{2}-(1810)^{2}}{k^{2}-1}}}$

Remplaçons les données par leurs valeurs:

$\displaystyle{x=\sqrt{\frac{(\frac{0.79}{0.29})^{2}\cdot (1050)^{2}-(1810)^{2}}{(\frac{0.79}{0.29})^{2}-1}}}$

$x=874.0605963$

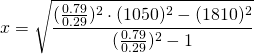
On arrondit:

$x=874\; m$

SURFACES:

Les autres côtés:

$d_{1}=\sqrt{(1810)^{2}-x^{2}}$

$d_{1}=\sqrt{(1810)^{2}-(874.0605963)^{2}}$

$d_{1}=1584.966269$

$d_{1}=1585\;m$

$d_{2}=\sqrt{(1810)^{2}-x^{2}}-\sqrt{(1050)^{2}-x^{2}}$

$d_{2}=\sqrt{(1810)^{2}-(874.0605963)^{2}}-\sqrt{(1050)^{2}-(874.0605963)^{2}}$

$d_{2}=1003.143208$

$d_{2}=1003\;m$

L’aire du $\triangle ABC=\frac{1}{2}x\cdot d_{1}$

L’aire du $\triangle ABC=\frac{1}{2}\times 874.0605963\times 1584.966269$

L’aire du $\triangle ABC=692678.2811$

En arrondissant:

$\mathcal{A}\;\triangle ABC=692678 \;m^{2}$

$SURFACE\; TOTALE:$

Le trapèze:

$\mathcal{A}\; \square ABCD=\frac{d_{1}+d_{2}}{2}\cdot x$

$\mathcal{A}\; \square ABCD=\frac{1584.966269+1003.143208}{2}\times 874.0605963$

$\mathcal{A}\; \square ABCD=1131082.256$

$\mathcal{A}\; ABCD=1131082\;m^{2}$

$AIRE\; D'UNE\; PARCELLE:\; 5160\; PARCELLES$

$mathcal{A} \;parcelle=\frac{1131082}{5160}$

$mathcal{A} \;Parcelle=219\;m^{2}$

Formule de Heron pour le 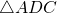$\triangle ADC$

Calculons $d_{2}$

$\displaystyle{\frac{\sin {\alpha}}{1050}=\frac{\sin {\beta}}{d_{2}} \Rightarrow d_{2}=1050 \cdot \frac{\sin {\beta}}{\sin {\alpha}}}$

$\displaystyle{d_{2}=1050 \cdot \frac{\sin {27^{\circ}.47467203}}{\sin {28^{\circ}.8753967}}}$

$d_{2}=1003.143208$

Les côtés: $1050$ , $1810$ , $1003.143208$

Calculons $s$ :

$s=\frac{1050+1810+1003.143208}{2}$

$s=1931.571604$

$s-1050=1931.571604-1050=881.571604$

$s-1810=1931.571604-1810=121.571604$

$s-1003.143208=1931.571604-1003.143208=928.428396$

L’aire $\displaystyle{\mathcal{A}\;\triangle ADC=\sqrt{1931.571604 \times 881.571604 \times 121.571604 \times 928.428396 }}$

L’aire $\mathcal{A}\;\triangle ADC=438403.9751$

En arrondissant:

L’aire $\mathcal{A}\triangle ADC=438404\; m^{2}$

Post Views: 159

Challenge 1 Spring of 2017: Solution Trapèze par méthode Algébrique

Promotion de la Géometrie élémentaire

PROBLEME 2: LE TRAPEZE

SOLUTION: Par méthode Algébrique

Formule de Heron pour le $\triangle ADC$

Be the first to comment

Leave a Reply Cancel reply