Quadratic Equations
Quadratic Equations
A quadratic equation is written in the following form:
These equations contain polynomials of the second degree, with the square being the highest exponent.
It is important that we find the values of the constants ![]() ,
, ![]() and
and ![]() . The standard form must be written in the above format.
. The standard form must be written in the above format.
The exponent of 2 must be present in order for it to be a quadratic equation. When the equation is given in another form, we can always re-arrange it to get ![]()
Example: ![]() We need to put this in the standard form:
We need to put this in the standard form:
![]()
![]()
Now multiply all by ![]() to get the standard form:
to get the standard form: ![]()
Please note that ![]() and
and ![]() can be
can be ![]() ,
, ![]() or
or ![]() .
.
1.Solving by Factoring:
We have used factoring in our examples in this site. Now we can see how we arrived at these factors.
Given :
Solve by factoring.
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} ax^2+bx+c&=a(x^2+\frac{b}{a}x+\frac{c}{a})\\ &=a\left[{(x+\frac{b}{2a})}^2-{(\frac{b}{2a})}^2+\frac{c}{a}\right]\\ &=a\left[{(x+\frac{b}{2a})}^2-\frac{b^2}{4a^2}+\frac{4ac}{4a^2}\right]\\ &=a\left[{(x+\frac{b}{2a})}^2-\frac{(b^2-4ac)}{4a^2}\right]\\ &=a\left[{(x+\frac{b}{2a})}^2-{(\frac{\sqrt{b^2-4ac}}{2a})}^2\right] \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-01a28772e3a1b8a8e12a97c63a084779_l3.png)
Now we have the difference of squares seen in the identities lesson:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} a\left[{\left(x+\frac{b}{2a}\right)}^2-{\left(\frac{\sqrt{b^2-4ac}}{2a}\right)}^2\right]&=a\left[\left(x+\frac{b}{2a}+\frac{\sqrt{b^2-4ac}}{2a}\right)\left(x+\frac{b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}\right)\right]\\ &=a\left[\left(x+\frac{b+\sqrt{b^2-4ac}}{2a}\right)\left(x+\frac{b-\sqrt{b^2-4ac}}{2a}\right)\right] \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-1276b788e0c70a4b5fcbf74dd0adee81_l3.png)
Going back to our equation:
![]()
Finally we get:
From ![]()
![]()
Any of the two factors will define one solution.
The two values of ![]() are:
are:
Solved by factoring.
2. Further Factoring methods
It may so happen that the roots are simple integers easy to find. We use the following method for factoring.
If we have ![]() We can try to find two values such:
We can try to find two values such:
-Their sum is ![]() -Their product is
-Their product is ![]() Then we rewrite our expression by replacing
Then we rewrite our expression by replacing ![]() by these two numbers. Example:
by these two numbers. Example:
Factor:
![]()
Here
![]()
![]()
![]()
Find 2 numbers with a sum of ![]() and a product of
and a product of ![]() .
.
With experience, we see that ![]() and
and ![]() are the two numbers.
are the two numbers.
Now we write:
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} 5x^2-21x-20&=5x^2-25x+4x-20\\&=(5x^2-25x)+(4x-20)\\ &=\left[5x(x-5)+4(x-5)\right]\\&=(x-5)(5x+4) \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-be6051a12f0aa2123598c31323e425a7_l3.png)
Finally: ![]()
3- Using the quadratic formula
To solve ![]() , we are not going to factor every time. We use the formula we discovered earlier.
, we are not going to factor every time. We use the formula we discovered earlier.
let’s use a discriminant ![]() such:
such: ![]()
From part 1 we get the following case:
-When ![]() we have two roots for solution
we have two roots for solution
![]()
-When ![]() we have a duplicate root for solution
we have a duplicate root for solution
![]()
–When ![]() there is no root in the real number system
there is no root in the real number system
(Since we do not have a square root for a negative number).
4. Completing the square:
We have nearly used it in part 1. We have to isolate the ![]() by moving everything else to the right side.
by moving everything else to the right side.
![]()
![]()
But we know from identities that:
![]()
So we simply get: ![]()
Then
![]()
![]()
![]()
![]()
Finally, the solution with the two possible roots:
![]()
Example:Solve by completing the square:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Answer: ![]()
Relationships between the roots of a quadratic equation
When the equation has two roots ![]() and
and ![]() in
in ![]() , we can note the following:
, we can note the following:
Sum of the roots
(4) 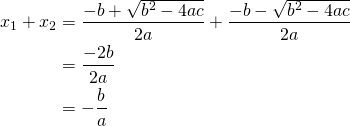
Finally:
![]()
The product of the roots
(5) 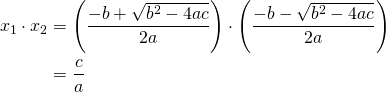
Finally:
![]()
Solve for ![]()
![]()
Please note that ![]()
let ![]()
We get:
![]()
Here:
![]()
![]()
![]()
(6) ![]()
![]()
Since ![]() we plug in:
we plug in:
![]()
![]()
![]()
![]()
Since ![]() we plug in:
we plug in:
![]()
![]()
![]()
![]()
Solve for ![]() :
:
![]()
We proceed by grouping:
![]()
![]()
![]()
![]()
Two cases:
![]()
This is the only solution:
Answer: ![]()
Solve for ![]()
![]()
Let ![]()
We get:
![]()
![]()
![]()
![]()
(7) 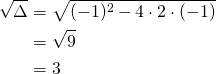
![]()
But ![]()
![]()
![]()
But ![]()
![]()
Answer: ![]()
Solve for ![]()
![]()
But when we can factor: ![]()
The Equation becomes: ![]() with
with ![]()
By using the common denominator: ![]()
![]()
![]()
![]()
The roots:
![]()
Not acceptable
![]()
Answer: ![]()
Solve for ![]()
![]()
Squaring both sides ![]()
![]()
Squaring one more time ![]()
![]()
![]()
Verification shows ![]() on each side.
on each side.
Answer: ![]()
Quadratic functions
A quadratic function has the form
![]()
As we have already seen, a,b and c are real numbers with ![]()
The domain of the quadratic function is the set of all real numbers. ![]() is defined for any value of
is defined for any value of ![]() .
.
![]()
Or simple:
![]() .
.
In the previous paragraphs, we solved the quadratic for ![]() . We can use the same concept here in graphing the quadratic functions.
. We can use the same concept here in graphing the quadratic functions.
x-intercepts:
These are the solutions found by solving ![]() . We’ll see that this statement is the
. We’ll see that this statement is the ![]() . The value of
. The value of ![]() is
is ![]() anywhere in this axis.
anywhere in this axis.
So we have 3 possibilities:
When ![]() is
is ![]() , we had two values as roots. In graphing, the function crosses the
, we had two values as roots. In graphing, the function crosses the ![]() at these 2 points.
at these 2 points.

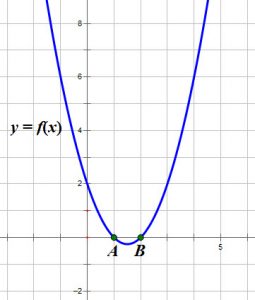
When ![]() is
is ![]() , the function touches the
, the function touches the ![]() at that point.
at that point.
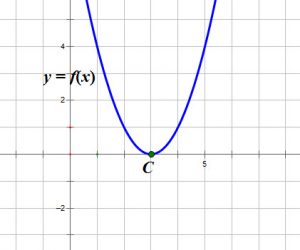
When ![]() is
is ![]() , the function never crosses or touches the
, the function never crosses or touches the ![]() .
.
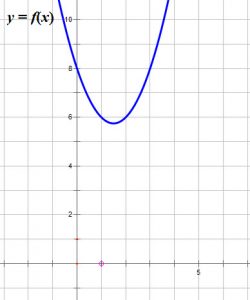
The ![]() is where the function crosses the
is where the function crosses the ![]() .
.

We can get it by making the variable ![]() equal to
equal to ![]() .
.
We need to re-write these functions in the following format
(8) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} (ax^2+bx+c)&=\left[a \left(x+\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2+\frac{c}{a}\right]\\ &=a\left(x+\frac{b}{2a}\right)^2+\frac{4ac-b^2}{4a} \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-109723f9d837bf7ff13341a1a17019de_l3.png)
Let ![]()
And
![]()
The function can be written:
![]()
In graphing we’ll see that the point ![]() is the vertex of the function.
is the vertex of the function.
This is the point that defines the axis of symmetry.
![]() is a vertical line that is the axis of symmetry of the function.
is a vertical line that is the axis of symmetry of the function.
Example
Graph ![]()
![]()
![]()
And ![]()
![]()
We re-write:
![]()
The vertex is ![]()
y-intercept: When ![]() ,
, ![]()
x-intercept:
The solutions:
![]()
It touches the ![]() at the vertex.
at the vertex.
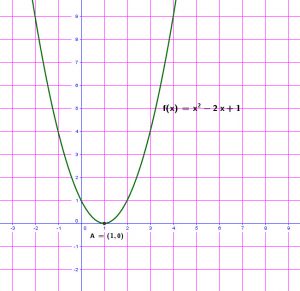

Graphs variations
If we are using the form ![]() , we need to know how to graph these functions without long logics.
, we need to know how to graph these functions without long logics.
Let’s go from the base:
![]()

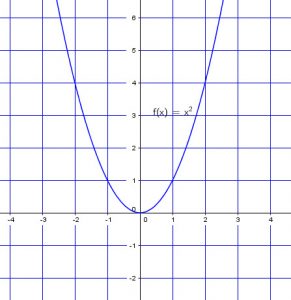
Now for ![]() , we just have to move this original graph 1 unit to the right.
, we just have to move this original graph 1 unit to the right.

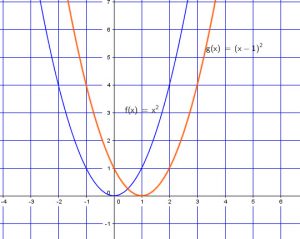
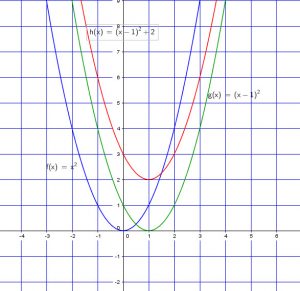
Now let’s add to the y-coordinate
![]() , we just move the graph two units up.
, we just move the graph two units up.

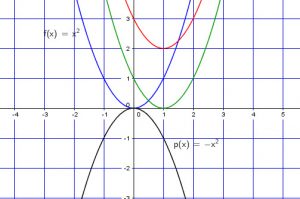
Now if we change the sign of ![]()
![]() . The function is flipped about the
. The function is flipped about the ![]() . It is the mirror of the original.
. It is the mirror of the original.

Now let’s make ![]() from the original
from the original
![]()

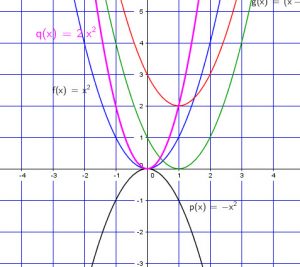
We can now say:
-If![]() we flip the original before moving
we flip the original before moving
-If ![]() , we move the original to the right by
, we move the original to the right by ![]() units.
units.
-If ![]() , we move the original to the left by
, we move the original to the left by ![]() units.
units.
-If ![]() , we move the original up by
, we move the original up by ![]() units.
units.
-If ![]() , we move the original down by
, we move the original down by ![]() units.
units.
-If ![]() the graph is narrower
the graph is narrower
-If ![]() the graph is wider.
the graph is wider.
Example:
![]()
From ![]() ,
,
flip, move 3 units to the left, move 2 units down. Graph is wider.

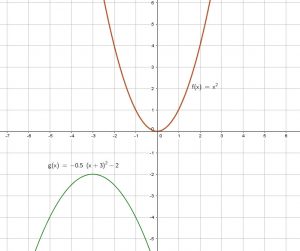
Grph the function:
![]()

Problem 1
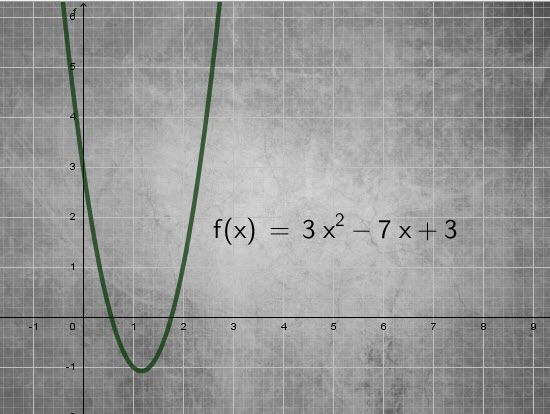
A certain equation has been graphed as follows. Please find the equation in the form of ![]()

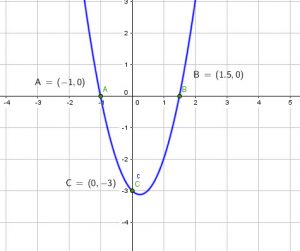
Solution:
Click on the following to watch the video for the solution
Problem 2:
Given the following equation:
1. What values of ![]() make this equation, an equation with 2 roots?
make this equation, an equation with 2 roots?
2. Find the values of ![]() so that the equation has only one root as a solution. Calculate the root in each case.
so that the equation has only one root as a solution. Calculate the root in each case.
3. Find all the values of ![]() making the equation one without a solution in
making the equation one without a solution in ![]() .
.
4. Find the values of ![]() that give a solution of 4 as one of the roots.
that give a solution of 4 as one of the roots.
5.Finally, find the values of ![]() making the product of the two roots
making the product of the two roots ![]() .
.
Solution:
Click here for the Solution in another post.
Problem 3:
Given the following equation:
1. Find the positive value of ![]() so that the equation has only one root as a solution.
so that the equation has only one root as a solution.
2.Calculate the root.
Solution:
![]()
For a double solution, the discriminant ![]() must be
must be ![]()
![]()
![]()
![]()
![]()
This is the only value per the prompt.
For ![]() we get:
we get:
![]()
![]()
![]()


Be the first to comment