Inequalities

Inequalities appear to us in many forms.

Imagine that we want to express the following sentence in an equation:

The total number of cars parked here is at least 50. If this total is $T$ , we can write:

$T \geq 50$ .
This is our first inequality.

Inequalities are sentences containing the verbs $>,\geq,< or \leq$

Solving inequalities require the same steps used to solve equation with two major differences.

-Multiplying both sides by the same negative value changes the orientation of the equality:
When we have $x>5$ , think that when we look at the number line, all values after 5 moving to the right are solution.
Now when we multiply by $-1$ , we must change the inequality:
We get $-x<-5$ . This is true because here the values are all on the left of $5$ .

Addition principle:

The inequalities can be treated the same way as the equations when adding or subtracting the same value from both sides.
If $x<y$ is $true$ then $x+u<y+u$ is also $true$ .
Two inequalities with the same solution are equivalent.

Four times a number $\Rightarrow 4n$
Seven less than a number $\Rightarrow n-7$
Five more than a number $\Rightarrow n+5$
The opposite of 9 $\Rightarrow -9$
NO MORE THAN a number $\Rightarrow$ LESS THAN OR EQUAL TO a number $\Rightarrow \leq n$
NO LESS THAN a number or GREATER THAN OR EQUAL TO a number $\Rightarrow \geq n$

Multiplication principle for inequalities:

If both sides of a true inequality are multiplied or divided by the same positive number, the inequality remains true.

However, when multiplied or divided by the same negative number, the inequality symbol is reversed.

The inequality symbol is also reversed when we take the reciprocals of both sides.

For this introduction, we’ll solve inequalities and graph on the number line.

Compound inequalities:

Sometimes we have situations were two or more inequalities are joined by the words $and$ or $or$ .
Example: The temperature must be kept between 32 and 65.
We can write: $32<temp$ and $temp<65$ . We can join these two inequalities:
$32<temp<65$
We can easily graph this in our number line.
Sometimes we may need to solve them separately and graph the result. Remember that $and$ means both conditions must be met.
The $or$ is a disjunction. The solution here is the union of the individual solution sets.

Solving and graphing inequalities:

We’ll use the principles learnt here and solve some inequalities. We translate every solution to our number line.

When a solution is $>$ or is $<$ than a given number, the graphing on that point is a $\circ$ . Here the dot is not filled in.

If we have solution that is $\leq$ or is $\geq$ a certain number, the graphing on that point is a $\bullet$ . You fill in the dot.

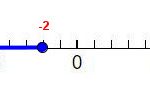
1. Graph on a number line:

$x \leq -2$

Solution

We have the following graph

2. Solve and graph on a number line:

$-7x < 28$

Solution

We have the following:

$-7x < 28$

$\frac{-7x}{-7} >\frac{28}{-7}$ Dividing by $-7$ changes the inequality.

$x>-4$

3. Solve

A theather is offering a sale on tickets to a group of students in 2 ways.

A. An initial fee of 35.00 dollars and any tickets costs only 5.00 dollars.

B. A flat price without initial fee. The tickets costs 6.75 dollars.

What numbers of student make the way $A$ cheaper than way $B$ ?

Solution

We just setup the inequality and solve:

If $N$ is the number of students,

$35+5N$ must be less than $6.75N$

We have:

$35+5N<6.75N$

$35+5N-5N<6.75N-5N$

$35<1.75N$

$\frac{35}{1.75}<\frac{1.75N}{1.75}$

$20<N$

$N>20$

They have to be more than 20 to make way $A$ cheaper.

4. Solve and graph on a number line:

$-3(7x+2)\leq -25x+6$

Solution

We have the following:

$-3(7x+2)\leq -25x+6$

$-21x-6 \leq -25x+6$

$25x-21x-6+6 \leq -25x+25x+6+6$

$4x \leq 12$

$\frac{4x}{4}\leq \frac{12}{4}$

$x \leq 3$

5. Solve and graph on a number line:

$x <\frac{2}{3}x+\frac{1}{2}\leq x+3$

Solution

We have the following:

$x <\frac{2}{3}x+\frac{1}{2}\leq x+3$

Now the same denominator of 6 :

$6x<4x+3 \leq 6x+18$

$6x-3<4x+3-3 \leq 6x+18-3$

$6x-3<4x \leq 6x+15$

$6x-6x-3<4x-6x \leq 6x-6x+15$

$-3<-2x \leq 15$

$\frac{-3}{-2}>\frac{-2}{-2}x \geq \frac{15}{-2}$

$\frac{3}{2}>x \geq -\frac{15}{2}$

We can rewrite:

$-\frac{15}{2}<x \leq \frac{3}{2}$

6. Solve for $x$

$\frac{x-2}{x+3}\geq 0$

Solution

We have tout check the sign of the full part on the left and make sure it is $\geq 0$ .

We use the following table:

Factor	$x<-3$	$-3<x<2$	$x \geq 2$
$x-2$	$-$	$-$	$+$
$x+3$	$-$	$+$	$+$
$\frac{x-2}{x+3}$	$+$	$-$	$+$

We can see the solution:

When $x<-3$ and $x \geq 2$ the inequation is true.

Answer $\{x<-3, x \geq 2\}$

Additional inequalities solving for lower grades:

1. Say: $5-2x>-4$

5 minus two times a number is greater than the opposite of 4.

2. Write: “Three times a number minus 7 is less than or equal to the opposite of 10”

$3x-7 \leq -10$

3. Four times a number is at least 2

$4x \geq 2$

4. One third of the opposite of a number is less than 12.

$1/3 (-x)<12$ or $-x/3<12$

5. A number increased by 5 is less than 7

$x+5<7$

6. Ten less than a number is more than 30

$n-10>30$

7. Two more than 5 times a number is greater or equal to 3

$5x+2 \geq 3$

8. Six less than two times a number is no more than 17

NO MORE: Means less than or equal to.

$2x-6 \leq17$

9. A video game enthusiast saved $750 to spend on a video game player and games.
The player costs $400. the games costs $49 each. At most, how many games can he buy along with the player?

If $x$ is the number of games:
$49x \leq 750-400$
$49x \leq 350$
$x \leq \frac{350}{49}$
$x \leq 7,...$
He can buy 7 games.

10. A health-food producer has 250 samples of a new snack to distribute in the mall.
The producer has to keep AT LEAST 50 samples for display in the store. How long will the samples last if
consumes are taking the samples at the rate of 25 every hour?

$n$ total number of distributed samples

$250-n \geq 50$ or $50 \leq 250-n$

We solve:
$250-n \geq 50$

We multiply by -1 and we flip:
$n-250 \leq -50$

$n-250+250 \leq -50+250$
n<=200

For the number of hours: $h=\frac{n}{25} \Rightarrow n=25h$

We plugin

$25h \leq 200$
$h \leq \frac{200}{25}$

$h \leq 8$
Time is 8 hours AT THE MOST.

11.Write and solve:

Arthur earned $136 in three weeks. He goes back to school in one more week.
He needs AT LEAST $189 to buy a new coat. How much must Arthur earn next week?

$136+n \geq 189$
$n \geq 53$
AT LEAST $53.00.

12. Mama is playing a game where you score less -5 points each time you guess a correct answer.
The goal is to get the lowest score. To win the game, Mama must have a score LESS THAN -80 points. How many correct answers does
Mama need to win the game?

$n$ the number of correct answers
$-5n<-80$
$5n>80$
$n>16.$
She needs to guess correctly more than 16 games.

13. Fifty students are trying to raise AT LEAST $12,500 for a class trip.
They have already raised $1,250.
How much should each student raise, on average, in order to meet their goal?

$x$ amount per student.
$50x+1250 \geq 12500$
$50x+1250-1250 \geq 12500-1250$
$\frac{50x}{50} \geq \frac{11250}{50}$
$x \geq 225$

14. At the end of the day, vegetables at farm market sell for $2.00 a pound, and a basket costs $3.50.
If Charlene wants to buy a basket and spend NO MORE THAN $10.00 total, how many pounds of vegetables can she buy?

NO MORE than $n$ means $\leq n$ .
If $p$ is the number of pounds:
$2p+3.50 \leq 10.00$
$2p+3.50-3.50 \leq 10.00-3.50$
$\frac{2p}{2} \leq \frac{6.50}{2}$
$p \leq 3.25$