Exercise:MD03CE

Hands-on: Pythagorean theorem:

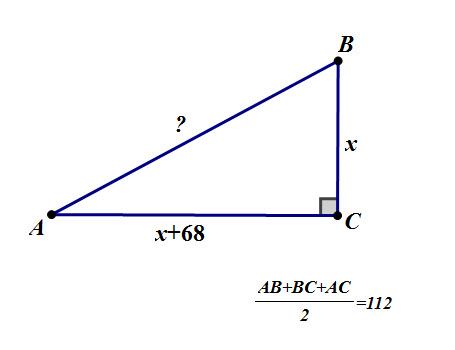
A right triangle has one of the legs 68 meters longer than the other. The semi-perimeter of the triangle is equal to 112 meters.
Find the hypotenuse and the two legs.

Calculate the area of the triangle.

Solution:

Let $x$ be the smallest leg.
The second leg is $x+68$
The hypotenuse is $\sqrt{x^2+(x+68)^2}$
The semi-perimeter is 112, meaning the perimeter is $112 \times 2=224$
We set the following equation:
$x+(x+68)+ \sqrt{x^2+(x+68)^2}=224$
$2x+68-224=\sqrt{x^2+(x+68)^2}$
$2x-156=\sqrt{x^2+(x+68)^2}$
$2(x-78)=\sqrt{x^2+(x+68)^2}$
$4(x-78)^2= x^2+(x+68)^2$
Now we take the squares :
$4(x^2-156x+78^2)=x^2+x^2+136x+68^2$
$4x^2-624x+24336=2x^2+136x+4624$
We get the quadratic equation:
$2x^2-760x+19712=0$
Simplifying:
$x^2-380x+9856=0$
We solve by Discrimant $\delta$
$\delta=(-380)^2-4 \times 1 \times 9856$
$\delta=104976$
$\sqrt{\delta}=324$
$x_1=\frac{380+324}{2}$
$x_1=352$
This value is not acceptable; the leg is longer than the given perimeter.
$x_2=\frac{380-324}{2}$
$x_2=28$
We use this value.
$x+68=96$
The hypotenuse:
$\sqrt{x^2+(x+68)^2}=\sqrt{28^2+(96)^2}$
$=100$
Finally we have the three sides:
$28, 96\;and \; 100$ .
The area of this triangle is merely:
$Area=\frac{28*96}{2}$
Area=1344 square meters.
—-The end—-

Post Views: 212

Solved Samples

Exercise:MD03CE

Hands-on: Pythagorean theorem:

Solution:

Be the first to comment

Leave a Reply Cancel reply