Graphes des fonctions exponentielles
La fonction ![]() est une fonction dont chaque valeur de la variable donne une simple valeur de la fonction.
est une fonction dont chaque valeur de la variable donne une simple valeur de la fonction.
Le domain de la fonction est de ![]() or
or ![]()
L’intersection avec l’axe des ![]() est de
est de ![]() . Il n’y a pas d’intersection de la courbe avec l’axe des
. Il n’y a pas d’intersection de la courbe avec l’axe des ![]() .
.
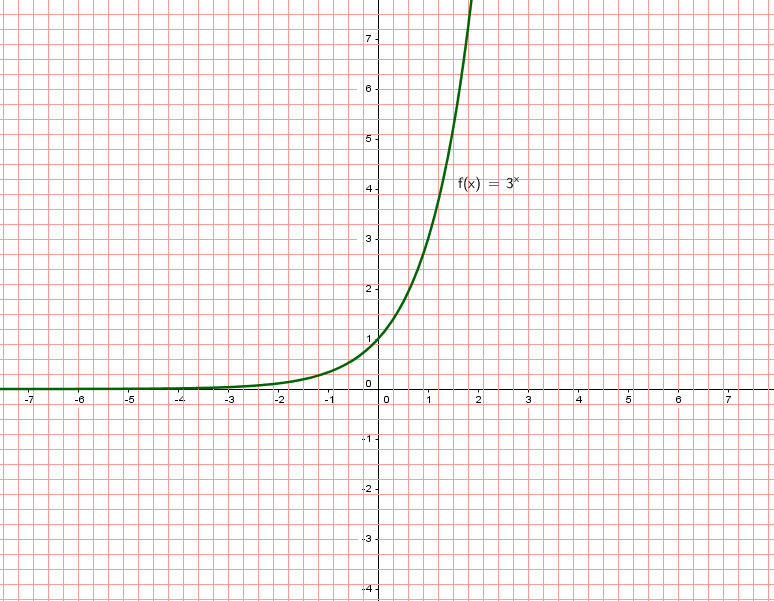
En approchant ![]() , la fonction s’approche de
, la fonction s’approche de ![]() mais quand on va vers la droite, la fonction croît vite.
mais quand on va vers la droite, la fonction croît vite.
Les règles de déplacement sont les mêmes que celles que nous avons vu avec les équations quadratiques.
Une reflexion autour de ![]() nous donne
nous donne ![]() . Si on déplace le graphe 4 unités vers le bas on obtient
. Si on déplace le graphe 4 unités vers le bas on obtient ![]()
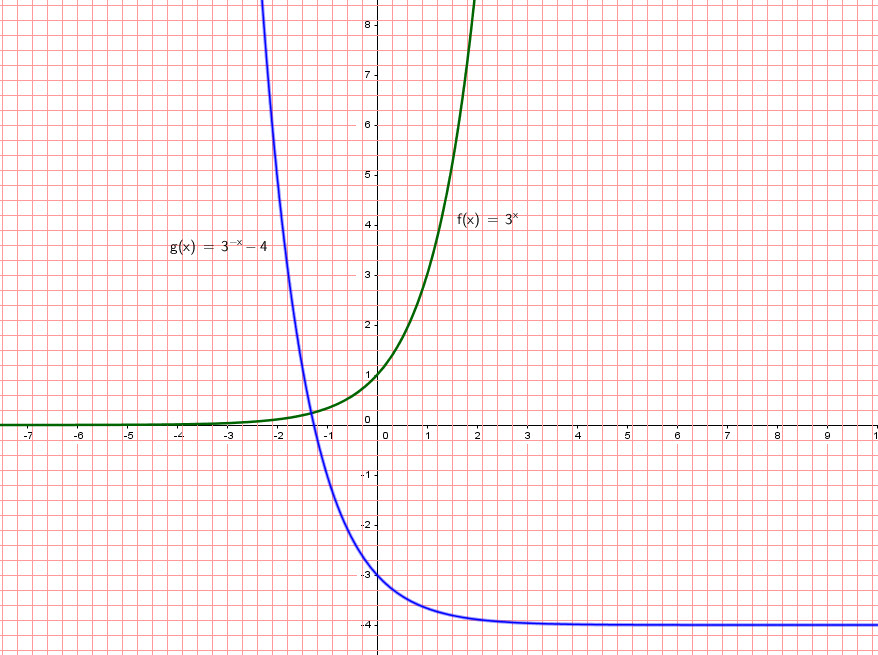
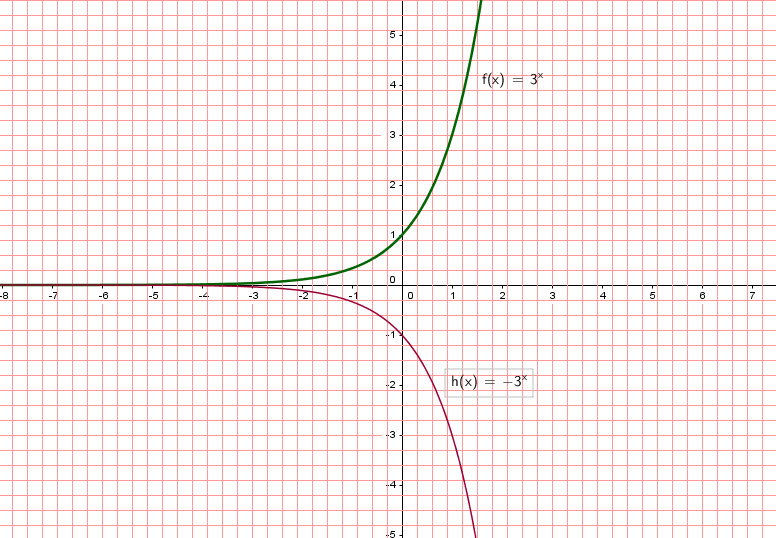
Le graphe de ![]() est une reflexion autour de l’axe des
est une reflexion autour de l’axe des ![]() .
.
Pour la base ![]() :
:
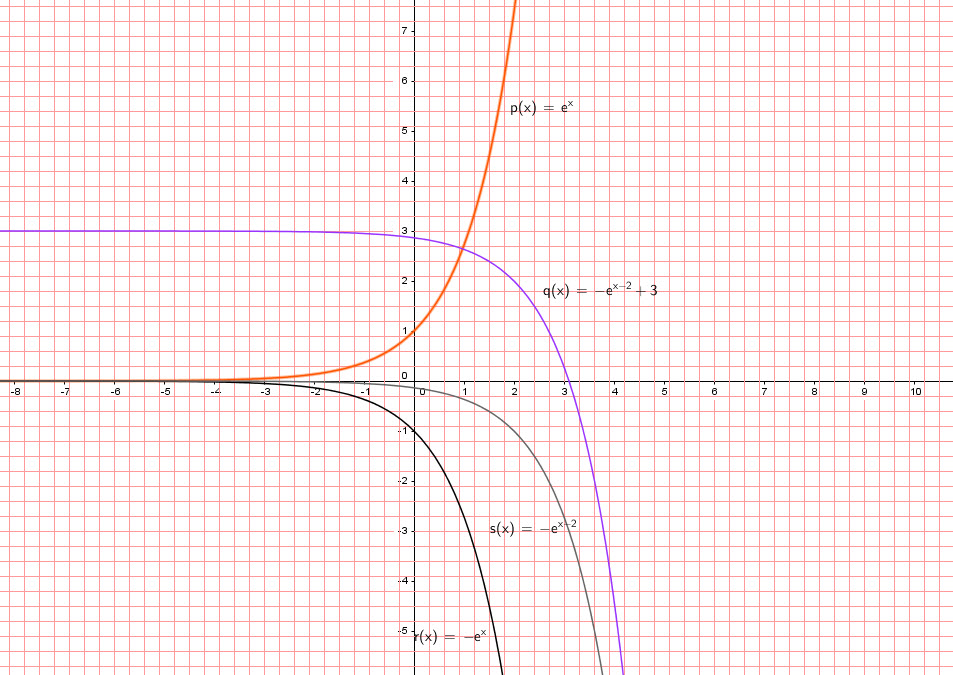
Nous faisons le graphe de ![]() et on utilise les transformations pour faire le graphe de
et on utilise les transformations pour faire le graphe de ![]()
Une reflexion autour de l’axe des ![]() , déplacement de 2 unités vers la droite et 3 unités en haut.
, déplacement de 2 unités vers la droite et 3 unités en haut.


Be the first to comment