Exponentielle et logarithme, pages multiples

Résoudre en $x$

$x=\log_{125}5$

nous prenons l’exposant 125 des deux membres:
$125^{x}=125^{\log_{125}5}$

Simplifiant:
$125^{x}=5$
$5^{3x}=5^{1}$
$3x=1$
$x=\frac{1}{3}$

Réponse: $x=\frac{1}{3}$

Résoudre $x$

$6=\log_{3}x$

Nous avons:
$3^6=x$
$x=729$

Réponse: $x=729$

[/item] [/accordion]

Résoudre en $x$

$10^x=\frac{1}{500}$

[accordion hideSpeed=”300″ showSpeed=”400″]

[item title=”Cliquer ici pour voir la solution de: $10^x=\frac{1}{500}$ “]

$10^x=\frac{2}{1000}$
$10^x=\frac{2}{10^3}$
$10^x=2\times 10^{-3}$
$x=\log_{10}(2\times 10^{-3})$
$x=\log_{10}(2)-3$
$x \approx -2.69897$

Résoudre en $x$

$2x=\log_{5}25$

Nous pouvons écrivons:
$x=\frac{1}{2}\log_{5}25$
$x=\log_{5}25^{\frac{1}{2}}$
$x=\log_{5}5$
$x=1$

Réponse: $x=1$

Evaluer:
$\log_{8}8^{5}+3^{\log_{3}8}$

We can write:
$\log_{8}8^{5}+3^{\log_{3}8}=5+8$
$\log_{8}8^{5}+3^{\log_{3}8}=13$

Réponse: $\log_{8}8^{5}+3^{\log_{3}8}=13$

Résoudre en $x$
$1+5^{x}=360$

$5^{x}=359$
$x=log_{5}359$
$x=\frac{\ln 359}{\ln 5}$
$x\approx 3.6555$

Réponse: $x=\frac{\ln 359}{\ln 5}$

Résoudre en $x$

$2^{x+1}=30$

Nous avons:
$2^{x+1}=30$
$x+1=\log_{2}30$
$x=\frac{\ln 30}{\ln 2}-1$

$x=\frac{\ln(15\times 2)}{\ln 2}-1$
$x=\frac{\ln 15+ \ln 2}{\ln 2}-1$
$x=\frac{\ln 15}{\ln 2}+1-1$

Réponse: $x=\frac{\ln 15}{\ln 2}$

Résoudre en $x$ et arrondir au centième

$7^{-x}=0.022$

Nous avons:

$7^{-x}=0.022$
$x=-\log_{7}0.022$
$x=-\frac{\ln 0.022}{\ln 7}$
$x\approx 1.96$

Réponse: $x\approx 1.96$

Résoudre en $x$

$\log_{2^{x}}256=2$

Nous avons:
$\frac{\ln 256}{\ln (2^{x})}=2$
$\frac{\ln (2^{8})}{\ln (2^{x})}=2$
On simplifie:
$\frac{8}{x}=2$
$2x=8$
$x=4$

Réponse: $x=4$

Résoudre en $x$

$e^{2\ln x}=9$

[accordion hideSpeed=”300″ showSpeed=”400″]

[item title=”Cliquer ici pour voir la solution de: $e^{2\ln x}=9$ “]

Nous avons:

$e^{2\ln x}=9$

$e^{\ln x^{2}}=9$
$x^2=9$
$x=3$

Réponse: $x=3$

[/item] [/accordion]

Résoudre en $x$

$\log_{2}(x+3)=\log_{2}(x-3)+\log_{3}9+4^{\log_{4}3}$

Nous avons:
$\log_{2}(x+3)=\log_{2}(x-3)+\log_{3}9+4^{\log_{4}3}$

$\log_{2}(x+3)=\log_{2}(x-3)+\log_{3}3^{2}+3$
$\log_{2}(x+3)=\log_{2}(x-3)+2+3$
$\log_{2}(x+3)=\log_{2}(x-3)+5$
$\log_{2}(x+3)-\log_{2}(x-3)=5$
$\log_{2}\frac{x+3}{x-3}=5$
$\frac{x+3}{x-3}=2^{5}$
$\frac{x+3}{x-3}=32$
$x+3=32(x-3)$
$x+3=32x-96$
$31x=99$
$x=\frac{99}{31}$

Réponse: $x=\frac{99}{31}$

Résoudre en $x$

$5^{x}=0.0016$

En observant $0.0016$
Son inverse est de $625$
$625=5^4$

Retour à l’équation:
$5^{x}=5^{-4}$
Ce qui signifie:
$x=-4$

Finalement:

Réponse: $x=-4$

Résoudre en $x$

$9e^{-2x}=1$

$e^{-2x}=\frac{1}{9}$
$e^{-2x}=\frac{1}{3^{2}}$
$e^{-2x}=3^{-2}$
$-2x=\ln(3^{-2}$
$-2x=-2\ln3$

Finalement:
$x=\ln3$

Réponse: $x=\ln3$

Résoudre en $x$

$(e^{x}+1)(e^{\frac{x}{2}}-7)=0$

Posons: $e^{\frac{x}{2}}=t$

L’équation devient:
$(t^{2}+1)(t-7)=0$

Seulement une racine ici: $t^{2}+1$ est toujours $>0$
$t-7=0$
$t=7$
Retour sur la notation $x$ :

$e^{\frac{x}{2}}=t$
$e^{\frac{x}{2}}=7$
$\frac{x}{2}=\ln7$
$x=2\ln7$

Finalement:

Réponse: $x=2\ln7$

Résoudre en $x$ :

$2+2\log_{3}x=\log_{3}(26x+3)$

$\log_{3}(26x+3)-\log_{3}x^{2}=2$

$\log_{3}\frac{26x+3}{x^{2}}=\log_{3}3^{2}$

Nous avons:

$\frac{26x+3}{x^{2}}=9$

$26x+3=9x^{2}$

On arrange:

$9x^{2}-26x-3=0$

Nous obtenons:

$x_1=-\frac{1}{9}$ et $x_2=3$

Mais $x$ doit être $>0$

La solution est de : $x=3$

Résoudre en $x$

$\ln(x-2)+\ln(x+1)=\ln(3x-5)$

Nous savons que:
$\ln(x-2)+\ln(x+1)=\ln{(x-2)(x+1)}$
Mais:
$(x-2)(x+1)=x^2-x-2$
L’équation devient:
$\ln(x-2)+\ln(x+1)=\ln(3x-5)$
$\ln{(x-2)(x+1)}=\ln(3x-5)$
En prenant l’exposant des deux membres:
$(x-2)(x+1)=3x-5$
$x^2-x-2=3x-5$
$x^2-x-2-3x+5=3x-5-3x+5$
$x^2-4x+3=0$

Pour factoriser, on doit trouver deux nombres ayant la somme de $-4$ et un produit de $3$ .

Ces deux nombres sont $-1$ et $-3$

En appliquant:

$x^2-4x+3=0$
$x^2-3x-x+3=0$
$x(x-3)-1(x-3)=0$
$(x-1)(x-3)=0$
Les deux racines sont:
$x=1$

Ceci ne marchera pas car nous devons prendre $\ln(1-2)$ qui n’est pas possible.

Ensuite $x=3$
Cette solution vérifie l’équation.

Finalement:

Réponse: $x=3$ .

Résoudre en $x$

$\ln|x+1|+\ln|x-5|=\ln16$

$\ln|(x+1)(x-5)|=\ln16$

Nous avons:
$(x+1)(x-5)=16$ , Seul cas car l’autre solution n’est pas valide.
$x^2-4x-5=16$
$x^2-4x-21=0$

Trouver deux nombres ayant une somme de $-4$ et un produit de $-21$ . Ce sont $-7$ et $3$ .
L’équation devient:
$x^2-7x+3x-21=0$
$x(x-7)+3(x-7)=0$
$(x+3)(x-7)=0$

Les racines:
$x=-3$
Bonne solution.
$\ln|-3+1|+\ln|-3-5|=\ln2+\ln8=\ln16$

La seconde racine:
$x=7$
Cette racine aussi vérifie l’équation.

Finalement:
La solution est de $x=-3$ et $x=7$

Résoudre en $x$ :

$6\ln^{2}x+7\ln(x)-3=0$

Changement de variable: $\ln(x)=t$
Nous avons:
$6t^2+7t-3=0$

Trouvons deux nombres ayant une somme de $7$ and a produit de $-18$ . Ces nombres sont $9$ et $-2$

L’équation devient:
$6t^2-2t+9t-3=0$
$2t(3t-1)+3(3t-1)=0$
$(2t+3)(3t-1)=0$
Les racines:
$2t+3=0$
$2t=-3$
$t=-\frac{3}{2}$
Pour: $\ln(x)=-\frac{3}{2}$
Nous avons:
$x=e^{-\frac{3}{2}}$
$x=\frac{1}{\sqrt{e^3}}$

Seconde racine:
$3t-1=0$
$3t=1$
$t=\frac{1}{3}$

Avec $\ln(x)=\frac{1}{3}$ ,
Nous avons:
$x=e^{\frac{1}{3}}$
Nous pouvons aussi écrire:
$x=\sqrt[3]{e}$

Résoudre en $x$ :

$4^{x}-3(4^{-x})=8$

Nous avons:
$4^{x}-3(4^{-x})=8$

$4^{x}-\frac{3}{4^{x}}=8$

$4^{x}\cdot 4^{x}-3=8\cdot 4^{x}$

Changement de variable: $t=4^{x}$

Nous avons:

$t^2-8t-3=0$

$\Delta=64+12$

$\Delta=76$

$\sqrt{\Delta}=2\sqrt{19}$

$t_1=\frac{8+2\sqrt{19}}{2}$

Retournant en $x$

$4^{x}=\frac{8+2\sqrt{19}}{2}$

$x=\log_{4}(\frac{8+2\sqrt{19}}{2})$

$x=\log_{4}(4+\sqrt{19})$

L’autre racine $t$ est négative et sera rejettée.

Réponse: $x=\log_{4}(4+\sqrt{19})$

Résoudre en $x$ et $y$

$\begin{cases}{}x+y=65 \; (1)\\\ln(xy)=6\ln2 \; (2)\end{cases}$

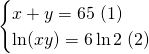
De (2) nous avons:

$\ln(xy)=6\ln2$
$\ln(xy)=\ln(2^{6})$
On obtient:
$xy=64$

De (1) nous avons:
$x+y=65$
$y=65-x$

Du nouveau (2):
$xy=64$
On remplace:
$x(65-x)=64$
$65x-x^2=64$
$x^2-65x+64=0$

Trouvons deux nombres dont la somme est de $-65$ et le produit $64$ . Ces nombres sont $-64$ et $-1$ .

$x^2-65x+64=0$

$x^2-x-64x+64=0$
$x(x-1)-64(x-1)=0$
$(x-64)(x-1)=0$
Les racines sont:
$x=64$
et $y=65-64=1$

Finalement:
La solution est de:
$x=64$ and $y=1$
Ou bien:
$x=1$ et $y=64$

Résoudre en $x$ et $y$

$\begin{cases}{}\ln(x^{3}y^{4})=6 \; (1)\\\ln(\frac{x^2}{y^5})=5; (2)\end{cases}$

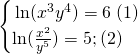
On écrit:
Pour (1):
$\ln(x^{3}y^{4})=6$
$\ln(x^3)+\ln(y^4)=6$
$3\ln(x)+4\ln(y)=6$

Pour (2):
$\ln(\frac{x^2}{y^5})=5$
$\ln(x^2)-\ln(y^5)=5$
$2\ln(x)-5\ln(y)=5$

Le système devient:
$\begin{cases}{}3\ln(x)+4\ln(y)=6\; (11)\\2\ln(x)-5\ln(y)=5; (22)\end{cases}$

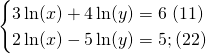
Par élimination, On multiplie (11) par $2$ et (12) par $-3$ et on les additionne.
$6\ln(x)+8\ln(y)=12$
$-6\ln(x)+15\ln(y)=-15$
Quand on ajoute:
$23\ln(y)=-3$
$ln(y)=-\frac{3}{23}$

$y=e^{-\frac{3}{23}}$
$y=\frac{1}{\sqrt[23]{e^3}}$

Maintenant éliminons $\ln(y)$

Par élimination, nous multiplions (11) par $5$ et (12) par $4$ et on additionne.
$15\ln(x)+20\ln(y)=30$
$8\ln(x)-20\ln(y)=20$
On obtient:
$23\ln(x)=50$
$ln(x)=-\frac{50}{23}$