An introduction to Complex numbers

Complex numbers are numbers in the form of $a+bi$ .

They are widely used and make lengthy solutions very short in various fields like Electrical Engineering, Navigation, etc…
In this form, $a$ and $b$ are real numbers. The unit $i$ is the imaginary unit . Please note that $i^2=-1$ .
Both $a$ and $b$ are real numbers.
If we take $z=a+bi$ , the real number $a$ is the $real \;part$ and the real part $b$ is the $imaginary \; part$ .

We may see:

$a=\Re(z)$ and $b=\Im(z)$

Around the 16th century, It became obvious that the solution of $x^2=-1$ would be handy.
When representing the image of a complex number in the $complex \; plane$ , the real part is projected in the $x-axis$ while the imaginary part will be projected in the $y-axis$ .
The quadrant rules we saw in earlier chapters remain the same.
An imaginary number is a number in the form $bi$ where $b$ is a real number.

$i=\sqrt{-1}$

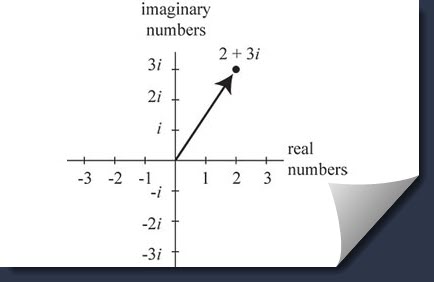
When a complex number has two components, we can represent it in the complex plane. This is called the Argand Diagram.

A point $(a,b)$ will then represent the complex number $a+bi$ .
We can call the $x-axis$ , the $real-axis$ and the $y-axis$ the $imaginary-axis$ .
A point $z=a+bi$ may be thought as a vector too. Adding $z$ to another complex number is a simple translation by vector $\vec(a,b)$
$z_2 \rightarrow z+z_1$ is a translation $a$ units to the right and $b$ units up in the complex plane.

Equality of complex numbers

For two complex numbers to be equal:

$a+bi=c+di$

we need to have the following:

$a=c$ and $b=d$

Example1:

$x+3i=5+yi$ means:

$x=5$ and $y=3$

Example2:

Find the values of $x$ and $y$ , the real numbers in the following equation:

$(x-3)+2i=8+yi$

We have:

$x-3=8$ , Real part

$x-3+3=8+3$

$x=11$

$y=2$ , Imaginary part

Finally:

Answer: $x=11$ and $y=2$

Addition and subtraction of complex numbers

To get the sum or difference, we add or subtract real parts, then we add and subtract imaginary parts:

$z_1=2-3i$

$z_2=3+4i$

$z_1+z_2=(2-3i)+(3+4i)=(2+3)+(-3+4)i=5+i$

Product of complex numbers

If $z_1=a+bi$ and $z_2=c+di$

$z_1z_2=(a+bi)(c+di)=ac+adi+bci+bdi^{2}$

$z_1z_2=ac+(ad+bc)i-bd=(ac-bd)+(ad+bc)i$

Example:

$(1+2i)(3-4i)=3-8i^{2}+(6-4)i=(3+8)+(6-4)i=11+2i$

Conjugate of a complex number

If $z=a+bi$ is a complex number, its conjugate is noted $\overline{z}=a-bi$

It can be represented as follows:

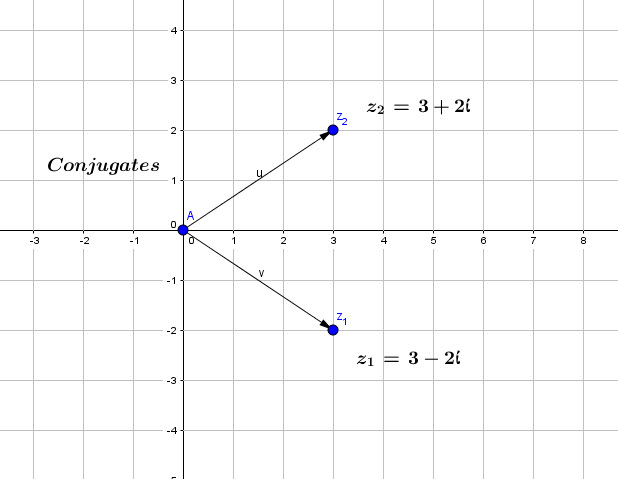
we can also note that:
$\overline{a+bi}=a-bi$

If we consider a quadratic equation with $b^2-4ac<0$ , having two complex roots,we can easily see that these two roots are $conjugate$ pairs.

Properties of conjugates:

The sum and product of a complex number and its conjugate are real numbers.

$(a+bi)+(a-bi)=2a$

$(a+bi)(a-bi)=a^{2}+b^{2}$

$\Re(z)=\Re(\overline{z})$

$\Im(z)=-\Im(\overline{z})$

$\arg(z)=-\arg(\overline{z})$

$|z|=|\overline{z}|$

$z+\overline{z}=2a=2\Re(z)$

$z-\overline{z}=2bi=2\Im(z)$

$\frac{1}{z}=\frac{\overline{z}}{|z|^{2}}$

Examples:

$(1+2i)+(1-2i)=2$

$(1+2i)(1-2i)=1^{2}+2^{2}=1+4=5$

Quotients of complex numbers

We have to multiply the complex number in the denominator by its conjugate.

Let’s calculate: $\frac{1}{a+bi}$

$\frac{1}{a+bi}=\frac{a-bi}{(a+bi)(a-bi)}=\frac{a-bi}{a^2+b^2}$

We can now write:
$(a+bi)^{-1}=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i$

Important:

For complex numbers $z$ and $v$ :

$\overline{z+v}=\overline{z}+\overline{v}$

$\overline{z \cdot v}=\overline{z} \cdot \overline{v}$

If the complex $v \neq 0$ , we can write:

$\overline {(\frac{z}{v})}=\frac{\overline{z}}{\overline{v}}$

Express in the form of $a+bi$ the following:

$\frac{3-i}{2-3i}$

Solution:

$\frac{3-i}{2-3i}=\frac{(3-i)(2+3i)}{(2-3i)(2+3i)}=\frac{(6-3i^{2})+(9-2)i}{2^{2}+3^{2}}=\frac{9+7i}{13}=\frac{9}{13}+\frac{7i}{13}$

Revisiting the quadratic equations

Solve for $x$ in $\mathbb{c}$

$z^3=1$

It means:
$z^3-1=0$

We know that:
$z^3-1=(z-1)(z^2+z+1)$

We get:

$(z-1)(z^2+z+1)=0$

First root: $z-1=0 \Rightarrow z=1$

Now we solve for the quadratic:

$z^2+z+1=0$

We have:
$\Delta=1^2-4\cdot 1 \cdot 1=-3$

However: $i^2=-1$

This means
$\Delta=3i^2$
$\sqrt{\Delta}=\sqrt{3}i$

$z_2=\frac{-1+\sqrt{3}i}{2}$

The third root is the conjugate:

$z_3=\frac{-1-\sqrt{3}i}{2}$

Finally:

Answer: $1$ , $\frac{-1+\sqrt{3}i}{2}$ and $\frac{-1-\sqrt{3}i}{2}$

1 2 3 4 5 6 7

Post Views: 549

An introduction to Complex numbers

An introduction to Complex numbers

Equality of complex numbers

Addition and subtraction of complex numbers

Product of complex numbers

Conjugate of a complex number

Properties of conjugates:

Quotients of complex numbers

Revisiting the quadratic equations

Be the first to comment

Leave a Reply Cancel reply