An introduction to Complex numbers

Introduction to vectors and polar coordinates

Vectors:

Vectors are widely used in navigation, physics, engineering etc…
The vector is always defined by its magnitude (the length of the vector or size) and its direction.
A simple example is a ship steering a certain course at a certain speed. The vector obtained is very useful in collision avoidance calculation.
Without the direction, this magnitude is simply called a $scalar$ .

Vectors can be noted using the lowercase letters such $u$ or $v$ .
They can also be written $\overline{AB}$ . The length can then be $AB$ or $|\overline{AB}|$ .
For the vector $u$ , the length can be written $\overline{u}$ .
When adding vectors, we can use the angles and trigonometry or simply draw them.

This was just a quick introduction, we’ll discuss vectors in later chapters.

Polar coordinates 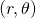$(r, \theta)$

In the plane, these are:
$r$ is the distance from origin and $\theta$ is the angle between $0$ and $2\pi$
Follow the trigonometric increase of angles, counter-clockwise.

$\theta \in \left [0, 2 \pi \right)$ .

Please note that:

$\left(-r, \theta \right)=\left(r, \theta+ \pi \right)$

Please see the example of some points in the polar coordinates in the graph.

Polar and cartesian

For a point $A$ , we have $A(r, \theta)=A(x,y)$
We can see the relationship from our trigonometric functions:
$x=r\cos \theta$
$y=r\sin \theta$
Raising both to the square and adding we get:

$r^{2}=x^{2}+y^{2}$

We can also divide:

$\tan \theta=\frac{y}{x}$

We will this this quick intro in the complex numbers calculations.

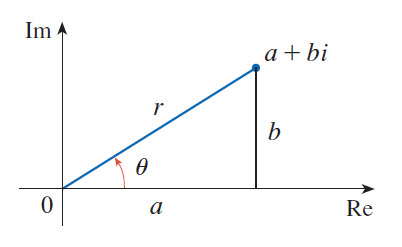
Modulus of a complex number

The $modulus$ of a complex number $z=x+yi$ is denoted by $|z|$ and is the distance between the origin and the point Z.
This is also the length of the vector corresponding to the complex $z$ .

For any complex number, we can write:
$|a \pm bi |=\sqrt{a^2+b2}$ . The distance is always $>0$ .

That yields:

$z\overline{z}=|z|^{2}$

We can also write the same equation:

$z^{-1}=\frac{\overline{z}}{|z|^2}$

Other formula:

$|z \cdot v|=|z|\cdot |v|$

$|z \cdot v|^{2}=|z|^{2}\cdot |v|^{2}$

$|z^{-1}|=(|z|)^{-1}$ if $z \neq 0$

Argument of a complex number

The argument of a complex $z=a+bi$ is the angle $\theta$ between the real axis and the line connecting $z$ to $0$ .
It is called $arg(z)$ .

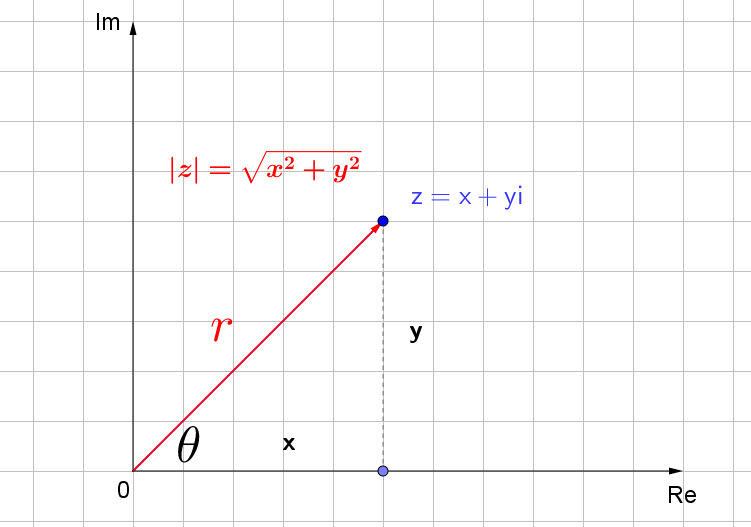
Polar-coordinate of complex numbers:

We have just seen the modulus and argument of complex numbers. These are the polar coordinates of the given complex number. As we’ll see soon, the polar coordinates are very useful in complex numbers calculation.

Let: $|z|=r$ and $arg(z)=\theta$ .

We can write:

$Re(z)=r\cos \theta$ and $\Im(z)=r\sin \theta$

Now $z$ is:

$z=r\cos \theta+i r \sin \theta$

After factoring:

$z=r(\cos \theta +i \sin \theta )$

We notice that when we use multiples of $2\pi$ , we will get a multi-valued Arg(z).

To come around that, we define the $principal \; value$ of $Arg(z)$ in the interval $(-\pi, \pi]$
So, for any complex $z$ we have the following:
$-\pi<Arg(z) \leq \pi$

Calculating 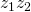$z_1z_2$ using polar coordinates

$z_1=r_1(\cos \theta +i \sin \theta)$

$z_2=r_2(\cos \phi +i \sin \phi)$

\begin{split}
z_1z_2&=r_1r_2(\cos \theta +i \sin \theta )(\cos \phi +i \sin \phi)\\
&=r_1r_2((\cos \theta \cos \phi+\sin \theta \sin \phi i^{2})+i(\cos \theta \sin \phi+\sin \theta \cos \phi)\\
&=r_1r_2(\cos(\theta +\phi)+i\sin(\cos(\theta +\phi)
\end{split}

This shows that the new modulus is the product of the moduli and the new argument is the sum of the arguments.

The following notation may be used:
$cis(\theta)=\cos \theta+ \sin \theta i$

1 2 3 4 5 6 7

Post Views: 568

Introduction to vectors and polar coordinates

Vectors:

Polar coordinates $(r, \theta)$

Polar and cartesian

Modulus of a complex number

Argument of a complex number

Polar-coordinate of complex numbers:

Calculating $z_1z_2$ using polar coordinates

Be the first to comment

Leave a Reply Cancel reply

Introduction to vectors and polar coordinates

Vectors:

Polar coordinates

Polar and cartesian

Modulus of a complex number

Argument of a complex number

Polar-coordinate of complex numbers:

Calculating using polar coordinates

Be the first to comment

Leave a Reply Cancel reply

Polar coordinates $(r, \theta)$

Calculating $z_1z_2$ using polar coordinates