An introduction to Complex numbers

Euler’s formula

Powers of 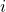$i$

$i^0=1$
$i^1=i$
$i^2=-1$
$i^3=-i$
$i^4=1$
$i^5=i$

In summary:

If $n$ is even and $n=2k$ , we can see that $i^n=i^{2k}=(i^2)^k=(-1)^k$
If $n$ is odd and $n=2k+1$ , we can see that $i^n=i^{2k}\cdot i=(i^2)^k=(-1)^k\cdot i$

Example:
$i^{203}$ We can say that $n=2k+1=203 \Rightarrow 2k=202$ here $k=101$ .
We get: $i^{203}=(-1)^{101}\cdot i=-i$

The polar coordinates of a complex number can be represented by a simpler form called Euler’s formula.

$\cos \theta+ \sin \theta i=e^{\theta i}$

This will have the following simplification:

$e^{z_1+z_2}=e^{z_1}\cdot e^{z_2}$

$e^{z_1z_2}=(e^{z_1})^{z_2}$

When $r>0$ we can write:

$z=r\cdot e^{\theta i}$

We can also have:

$z_1z_2=r_1r_2e^{(\theta_1+\theta_2)i}$

If we have $z=x+iy$ we can write:

$e^{z}=e^{x}e^{iy}$

Example:

$e^{i\pi}=-1$

$e^{i\frac{\pi}{2}}=i$

The Euler formulas:

$\cos (\theta)=\frac{e^{i\theta}+e^{-i\theta}}{2}$

$\sin (\theta)=\frac{e^{i\theta}-e^{-i\theta}}{2i}$

De Moivre’s theorem

If $n$ is a positive integer, then

$(\cos \theta+i\sin \theta)^{n}=\cos n\theta+i\sin n\theta$

If we have:

$z=r(\cos \theta+i\sin \theta)$

Then:

$z^n=r^n(\cos n\theta+i\sin n\theta)$

Example: $z^n=1$

This equation will have $n$ distinct roots:

$\mathbb{C}_k=e^{\frac{2k\pi i}{n}}$ with $k=0,1, \cdots, n-1$

These roots are equally spaced in the unit circle.

For:

$z^n=a$

Let $\phi$ be $arg(z)$

We write $a=|a|e^{i\phi}$

$z_k=|a|^{\frac{1}{n}}e^{i(\phi+2k\pi)}$

$k=0,1, \cdots, n-1$

Roots of a complex number

Using the skills learned from the De Moivre theorem, we can easily find the roots of complex numbers.
When $n>0$ and is a real number, we can find the $n^{th}$ root of any complex number. The roots form a regular polygon and in the case of the $unity$ , all roots lie in the $unit \; circle$ .
Through examples, we’ll show how easy it is to calculate these roots.

Example:

Calculate the roots of:
$z^2=1+i$

Use two methods.

First method:

We take $z=x+yi$
$z^2=(x+yi)^2$
$z^2=(x+yi)(x+yi)$
$z^2=x^2-y^2+2xyi$

But from the prompt: $z^2=1+i$

We get:
$x^2-y^2+2xyi=1+i$

Real parts must be equal and imaginary parts must be equal.

That yields:
$x^2-y^2=1$ and $2xy=1$

From the second equation:
$2xy=1 \Rightarrow 4x^2y^2=1$

But $x^2-y^2=1 \Rightarrow y^2=x^2-1$

We plug in:
$4x^2(x^2-1)=1$
$4x^4-4x^2=1$
$4x^4-4x^2-1=0$

$\Delta=16+16=32$

$x^2=\frac{4+\sqrt{16\cdot 2}}{8}$
$x^2=\frac{4+4\sqrt{2}}{8}$

$x^2=\frac{1+\sqrt{2}}{2}$ the other value is less than $0$
$x=\pm \sqrt{\frac{1+\sqrt{2}}{2}}$
$2xy=1 \Rightarrow y=\frac{1}{2x}$
$y=\pm \frac{1}{2 \cdot \sqrt{\frac{1+\sqrt{2}}{2}}}$

We can transform $y$ :

$y=\pm \frac{1}{\sqrt{2} \cdot \sqrt{1+\sqrt{2}}}$

Finally our solution:

Answer: $z=\pm (\sqrt{\frac{1+\sqrt{2}}{2}}+i\frac{1}{\sqrt{2} \cdot \sqrt{1+\sqrt{2}}})$

Second method:

$z^2=1+i$

$r=\sqrt{1^2+1^2}$

$r=\sqrt{2}$

$z^2=\sqrt{2}(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i)$

The base argument is $\theta=\frac{\pi}{4}$

The Euler’s formula:

$z^2=\sqrt{2}e^{i\frac{\pi}{4}}$

For the roots:

$z=(\sqrt{2})^{\frac{1}{2}}e^{i(\frac{\frac{\pi}{4}+2k\pi}{2})}$

$z=(\sqrt{2})^{\frac{1}{2}}e^{i(\frac{\pi}{8}+k\pi)}$

For $k=0$

$z=\sqrt{\sqrt{2}}e^{i(\frac{\pi}{8})}$

$z=\sqrt{\sqrt{2}}(\cos \frac{\pi}{8}+i \sin \frac{\pi}{8})$

But $\frac{\pi}{4}=2\frac{\pi}{8}$

We’ll see in trigonometry that:
$\cos 2\theta=\cos^{2}\theta-\sin^{2}\theta$

It means:
$\cos \theta=\sqrt{\frac{1+\cos 2\theta}{2}}$
$\sin \theta=\sqrt{\frac{1-\cos 2\theta}{2}}$

We know that:
$\cos \frac{\pi}{4}=\sin \frac{\pi}{4}=\frac{\sqrt{2}}{2}$
This gives:
$z=\sqrt{\sqrt{2}}(\sqrt{\frac{1+\frac{\sqrt{2}}{2}}{2}}+i\sqrt{\frac{1-\frac{\sqrt{2}}{2}}{2}})$

The real part:
When we put r under the radical:
$\sqrt{\sqrt{2}}(\sqrt{\frac{1+\frac{\sqrt{2}}{2}}{2}})=\sqrt{\frac{2\sqrt{2}+\sqrt{2}\cdot \sqrt{2}}{4}}=\sqrt{\frac{1+\sqrt{2}}{2}}$

The imaginary part:

When we put r under the radical:

$\sqrt{\sqrt{2}}(\sqrt{\frac{1-\frac{\sqrt{2}}{2}}{2}})=\sqrt{\frac{2\sqrt{2}-\sqrt{2}\cdot \sqrt{2}}{4}}=\sqrt{\frac{\sqrt{2}-1}{2}}$

Now we rationalize:
$\sqrt{\frac{\sqrt{2}-1}{2}}=\sqrt{\frac{(\sqrt{2}-1)(\sqrt{2}+1)}{2(\sqrt{2}+1)}}=\sqrt{\frac{1}{2(\sqrt{2}+1)}}=\frac{1}{\sqrt{2}\sqrt{\sqrt{2}+1}}$