An introduction to Complex numbers

Complex numbers and transformations

A transformation on the plane maps each point $M$ to its image $M'$ .
We can then associate each point to its affix. Let’s call these affixes $z$ and $z'$ , two complex numbers.

We can now write the transformation in complex terms:

$z'=f(z)$ where $f$ is the complex function associating $z$ to $z'$

Translation

For a vector $\vec{v}$ we have an affix $m$ .

We can simply write that:

$z'=z+m$

This simplifies to adding two vectors.

Let’s consider a point $A$ with affix $z_A=3+4i$
Now let’s translate it using $\vec{v}\binom 5{-3}$ .This is the same as adding it to the complex $5-3i$
We get another point $A'$ which is the image of $A$ with affix $z_{A'}$

$z_{A'}=z_A+5-3i$
$z_{A'}=3+4i+5-3i=8+i$

This can be used as a ship’s speed moving it along its course. Very solid concept.

Rotation from a complex number point of view

The Rotation must be centered at the origin $O$ . If $\theta$ is the angle of rotation:
The image of $z$ is

$z'=e^{i\theta}z$

This was the easiest case. Now, let’s take another center of rotation $\Omega$ with an affix $\omega$ .
The idea is to move the center of rotation to the origin $O$ .This is a simple translation by adding $-\omega$ first and then make the rotation and finally add $\omega$ to take the point to its original position.

$z'=e^{i\theta}(z-\omega)+\omega$

Example:

Simple rotation about $O$

A point $A$ with affix $z_A=1+i$ is rotated about the origin by $\frac{\pi}{4}$ , find the point $A'$ of affix $z_{A'}$ , image of $A$ after rotation.

$z_A=\sqrt{2}(cos \frac{\pi}{4}+ i \sin \frac{\pi}{4})$ , $\frac{\pi}{4}$ is the base angle.

In exponent expression:
$z_A=\sqrt{2}e^{i\frac{\pi}{4}}$

We use the rotation formula:
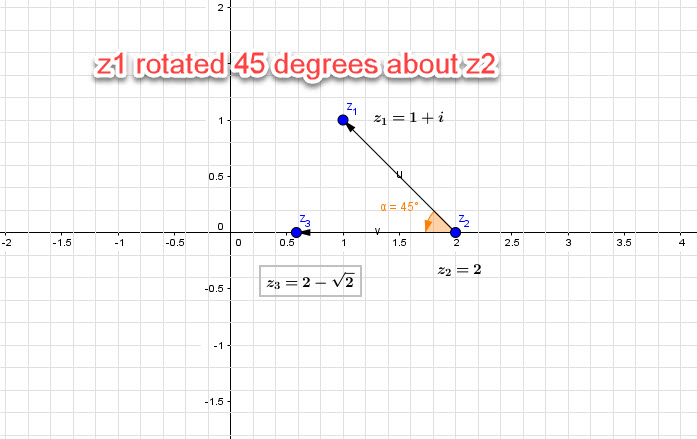
$z_{A'}=e^{i\frac{\pi}{4}}z_A=e^{i\frac{\pi}{4}}\cdot \sqrt{2}e^{i\frac{\pi}{4}}=\sqrt{2}e^{i(\frac{\pi}{4}+\frac{\pi}{4})}$
$z_{A'}=\sqrt{2}e^{i\frac{\pi}{2}}=\sqrt{2}(\cos \frac{\pi}{2}+i\sin \frac{\pi}{2})=i\sqrt{2}$

Rotation about any point

Now let’s rotate the point $A$ with affix $z_A=1+i$ about another point A point $\Omega$ with affix $\omega=2$ by $\frac{\pi}{4}$

we use our formula:
$z'=e^{i\theta}(z-\omega)+\omega$

$z_A-\omega=1+i-2=-1+i$

We can see that the resulting image:
$z'_A=-1+i=\sqrt{2}(cos \frac{3\pi}{4}+ i \sin \frac{3\pi}{4})$ , $\frac{3\pi}{4}$ is the base angle.
$z''_A=\sqrt{2}e^{i\frac{\pi}{4}}e^{i\frac{3\pi}{4}}+2=\sqrt{2}e^{i(\frac{\pi}{4}+\frac{3\pi}{4})}+2=\sqrt{2}e^{i\pi}+2=2+\sqrt{2}(cos \pi+ i \sin \pi)=2-\sqrt{2}$