Exercise:
![]()
![]()
Find ![]() ,
,![]() ,
,![]() and
and ![]()
Solution:
We notice that ![]()
![]()
![]()
![]()
![]()
Finally:
![]()
Evaluate:
![]()
Solution
Let ![]()
We try to find the polar expression:
The modulus:
![]()
Now for the argument:
if ![]() ,
,
![]()
![]()
We can see that ![]()
Now we can write:
![]()
Or even better:
![]()
Now the fabulous De Moivre formula
![]()
![]() But remember:
But remember: ![]()
So we get ![]()
![]()
![]()
![]()
![]()
Finally:
Answer: ![]()
Problem:
Find the 8th roots of ![]()
Solution:
![]() , finding the 8 roots
, finding the 8 roots
Let ![]()
![]()
Modulus:
![]()
![]()
We can write in polar form:
![]()
![]()
![]() here from
here from ![]() to
to ![]()
The roots:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finally:
Answer:![]()
Solve for ![]()
![]()
Solution
![]()
![]()
![]()
![]()
![]()
Our challenge is to find another complex number, the ![]()
Let ![]()
The modulus:
![]()
Now:
![]()
Base angle:
![]()
From our unit circle, the with both sine and cosine <0 is base angle plus 180 degrees.
![]()
However, our notation ![]() makes it
makes it ![]()
Now:
![]()
![]()
![]()
![]()
![]()
![]()
Finally:
Answer: ![]()
Problem:
Solve for ![]()
![]()
Solution
![]()
Let ![]()
Modulus:
![]() Please note that
Please note that ![]()
Now the arg(w)
![]()
From the unit circle:
The base angle here is ![]()
Now a combination of the trigonometric functions give ![]()
We need to find 3 roots with ![]()
The notation becomes:
![]()
Now:
![]()
The roots:
![]()
![]()
![]()
Some future formulas:
![]()
![]()
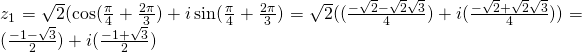
![]()
For ![]() we use the transformation formulas and we get:
we use the transformation formulas and we get:
![]()
![]()
Problem:
Evaluate ![]()
Solution
This can be done 2 ways
The peasant way,
Use binomial and note that this can be lengthy if the exponent is high
![]()
The poet way:
Use complex numbers operations. Always try this way.
![]()
Modulus:
![]()
![]()
The base angle: ![]() and is also the
and is also the ![]()
![]()
![]()
![]()
![]()
Finally:
Answer: ![]()
Problem:
Evaluate ![]()
Solution
![]()
The second method, more efficient for multiple comple numbers.
![]()
![]()
Base angle
![]()
With the ![]() showing
showing ![]() , we are in the first quadrant of the unit circle.
, we are in the first quadrant of the unit circle.
So, ![]()
![]()
![]()
Base angle
![]()
With the ![]() showing
showing ![]() , we are in the fourth quadrant of the unit circle.
, we are in the fourth quadrant of the unit circle.
So, ![]()
The product:
![]()
![]()
Answer: ![]()
Problem:
Evaluate ![]()
Solution
Two methods:
The first method
![]()
The second method, more efficient for multiple complex numbers.
![]()
![]()
Base angle
![]()
With the ![]() showing
showing ![]() , we are in the first quadrant of the unit circle.
, we are in the first quadrant of the unit circle.
So, ![]()
![]()
![]()
Base angle
![]()
With the ![]() showing
showing ![]() , we are in the fourth quadrant of the unit circle.
, we are in the fourth quadrant of the unit circle.
So, ![]()
![]()
![]()
Answer: ![]()
Problem:
Evaluate ![]()
Solution
![]()
For the conjugate we know:
![]()
Let ![]()
The values of the angle are exposed
We know that the modulus ![]()
![]()
That means:
![]()
![]()
This brings home:
![]()
Regular calculation:
![]()
Modulus ![]() and base angle:
and base angle: ![]() since we are in first quadrant.
since we are in first quadrant.
![]() But remember
But remember ![]()
That means:
![]()
Finally
Answer: ![]()
Exercise 27C (From EARL):
Let ![]()
Show that ![]() and deduce that
and deduce that ![]()
Find the quadratic equation with the roots ![]() and
and ![]() .
.
Hence show that ![]()
Our Approach and solution:
In the polar coordinates:
![]()
![]()
We know that:
![]()
This means:
![]()
To get 5 roots reals and complex, both factors must be equal to ![]()
We get:
![]()
To find the roots of the quadratic, let’s evaluate each element:
With in mind the argument ![]()
![]()
![]()
![]()
![]()
The roots are:
![]() and
and ![]()
The product:
![]()
![]()
This means we can change the following:
![]() to:
to:
![]()
![]()
When we convert:
![]()
![]()
Let ![]()
![]()
![]()
![]()
Before we go further, please note that ![]() since our angle is the first quadrant.
since our angle is the first quadrant.
![]()
Finally:
Answer: ![]()
Exercise 28C (EARL)
Determine the modulus and argument of the following complex numbers:
![]() and
and ![]() .
.
Calculate ![]() using polar coordinates and
using polar coordinates and ![]() form.
form.
Deduce the ![]() and
and ![]() .
.
Our Solution:
![]()
modulus:
![]()
![]()
![]()
![]()
![]()
modulus:
![]()
![]()
![]()
![]()
Now Calculating ![]()
![]()
![]()
In polar form:
![]()
![]()
![]()
Now we can say:
![]()
![]()
![]()
![]()
![]()
Finally
Answer: ![]() and
and ![]()
Exercise 30 B (EARL):
Using the 7th roots of -1 show that:
![]()
Use a similar process to evaluate:
![]()
Solution:
![]()
Modulus:
![]()
Argument:
![]() and
and ![]()
This means ![]()
![]()
The 7th roots:
![]() with
with ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Sum of roots is ![]()
![]()
This yields:
![]()
The same way, if we let:
![]() we get the following:
we get the following:
![]()
Finally:
![]()
![]()
Solve for ![]()
![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Click here to see the solution of: ![]() “]
“]
Solution:
![]()
![]()
![]()
Finally:
Answer: ![]()
[/item] [/accordion]
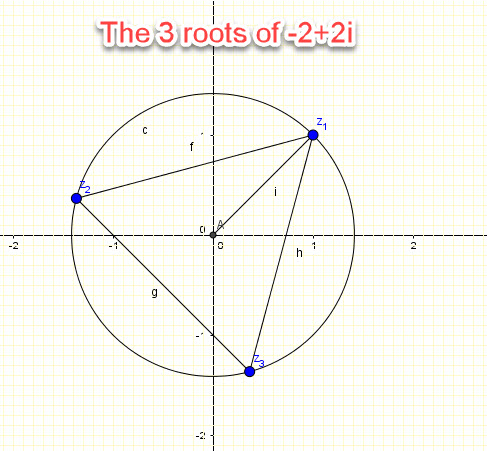
Solve ![]()
Draw the roots and calculate the area of the triangle formed by the three roots.
Solution:
Modulus:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finally:
Answers: ![]()
Write in ![]() form:
form:
![]()
Solution:
![]()
Please note ![]() is 1 radian or
is 1 radian or ![]() in degrees.
in degrees.
So:
![]()
Finally:
Answer: ![]()


Be the first to comment