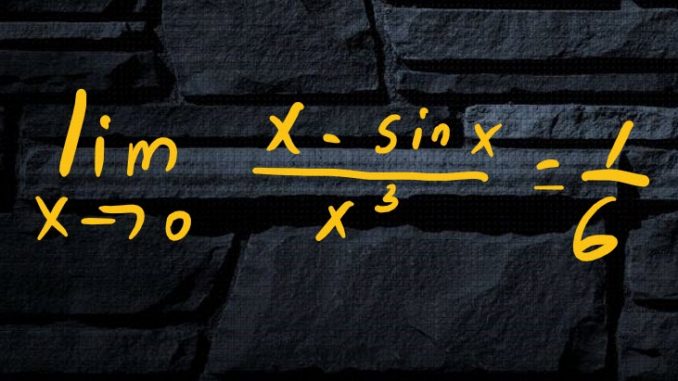
Dérivées d’ordre supérieur

Dans les formules qui suivent, nous montrons les Dérivées d’ordre supérieur avant de voir leur application.

Si on définit les fonctions $f(x)$ , $v(x)$ , $y(x)$ et $u(x)$ avec $x$ étant une variable et $n$ un nombre naturel:

$\frac{d}{dx}(u^{v})=vu^{v-1}\cdot \frac{du}{dx}+u^{v}\ln u \cdot\frac{dv}{dx}$

Composition:

$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$

On peut l’utiliser pour créer beaucoup de formules se trouvant dans les tables.

Exemple:

$y=(5x-8)^{4}$

Soit $u=5x-8$

Nous savons que:

$(u^{4})'=4u^{3}u'$

$\frac{du}{dx}=\frac{d}{dx}(5x-8)=5$

Finalement:

$\frac{d}{dx}((5x-8)^{4})=4(5x-8)\cdot 5=20(5x-8)$

Dérivation logarithmique:

Méthode permettant de trouver la dérivée de n’importe quelle fonction.

Utilisant la formule $\frac{d}{dx}(\ln u)=\frac{\frac{d}{dx}(u)}{u}$

On procède comme suit:

$y=f(x)$

$\ln y=\ln f(x)$

$(\ln y)'=(\ln f(x))'$

$\frac{y'}{y}=(\ln f(x))'$

$y'=y(\ln f(x))'$

$\frac{dy}{dx}=f(x)\cdot(\ln f(x))'$

Exemple:

Trouver la dérivée de:

$y=\sqrt[3]{3x^{2}}$

Solution:

$\ln y=\ln (\sqrt[3]{3x^{2}})$

$\ln y=\frac{1}{3}\ln(3x^{2})$

$\frac{y'}{y}=\frac{1}{3}\frac{6x}{3x^{2}}=\frac{2}{3x}$

$y'=y\frac{2}{3x}=\frac{2}{3x}\sqrt[3]{3x^{2}}$

Dérivée seconde

$f''=(f')'=\frac{d}{dx}(\frac{dy}{dx})=\frac{d^{y}}{dx^{2}}$

Ordre supérieur

$f^{(n)}=\frac{d^{n}y}{dx^{n}}$

$(u+v)^{(n)}=u^{(n)}+v^{(n)}$

$(u-v)^{(n)}=u^{(n)}-v^{(n)}$

Formules de Leibnitz

$(uv)^{'''}=u'''v+3u''v'+3u'v''+v'''$

$(uv)^{(n)}=u^{(n)}v+nu^{(n-1)}v'+\frac{n(n-1)}{1\cdot 2}u^{(n-2)}v''+\cdots +uv^{(n)}$

$(x^{m})^{(n)}=\frac{m!}{(m-n)!}x^{m-n}$

$(x^{n})^{(n)}=n!$

$(\log_{a}x)^{(n)}=\frac{(-1)^{n-1}(n-1)!}{x^{n} \ln a}$

$(\ln x)^{(n)}=\frac{(-1)^{n-1}(n-1)!}{x^{n}}$

$(a^{x})^{(n)}=a^{x} \ln a$

$(e^{x})^{(n)}=e^{x}$

$(a^{mx})^{(n)}=m^{n}a^{mx}\ln^{n}a$

$(\cos x)^{(n)}=\cos(x+\frac{n \pi}{2})$

$(\sin x)^{(n)}=\sin(x+\frac{n \pi}{2})$

Quelques Applications des dérivées:

Ce sera prétentieux de vouloir citer tous les cas d’utilisation des dérivées en quelques lignes. Cependant, avec des exercices appliqués, nous allons essayer de ressortir quelques aspects des différentielles.

Il faudra se souvenire que la dérivée n’est autre chose que la vitesse de changement des fonctions.

En conduisant une voiture, quand on accélère, la vitesse augmente à une certaine vitesse. Quand on arrête d’accélerer, la vitesse devient constante. Avant d’arriver, la vitesse diminue et la voiture s’immobilise.

La vitesse augmente, devient constante et diminue en s’ennulant vers la fin. Decription des différentielles. La vitesse de changement est positive, et la dérivée aussi pendant cette période. Le changement s’ennule et finalement devient négatif juste avant l’arrêt.

Valeur moyenne:

Si une fonction $f$ est continue sur $[a,b]$ et différentiable sur $(a,b)$ , alors $f(b)-f(a)=f'(c)(b-a)$ pour un certain nombre $c$ dans $(a,b)$ .

Corollaire :

Si $f'(x)=0$ pour tout $x$ dans $[a,b]$ , alors $f$ est constant sur $[a,b]$ , signifiant qu’il existe une $C$ telle que $f(x)=C$ pour tout $x$ dans $[a,b]$

Corollaire:

Soit $f$ une foction continue sur $[a,b]$ et différentiable sur $(a,b)$ :

Si $f'(x)>0$ pour tout $x$ dans $(a,b)$ , alors $f$ est une FOCTION CROISSANTE sur $[a,b]$

Si $f'(x)<0$ pour tout $x$ dans $(a,b)$ ,alors $f$ est une FOCTION DECROISSANTE sur $[a,b]$

Théorème de dérivée première:

Soit la fonction $f$ continue sur l’intervalle ouvert $(a,b)$ et différentiablesauf probablement en $c$

1.Si $f'(x)<0$ sur $(a,c)$ et $f'(x)>0$ sur $(c,b)$ , alors $f(c)$ est le minimum de $f$ sur $(a,b)$

2.Si $f'(x)>0$ sur $(a,c)$ et $f'(x)<0$ sur $(c,b)$ , alors $f(c)$ est le maximum def $f$ sur $(a,b)$

3. Si $f'(x)>0$ sur $f'(x)<0$ pour tout $x$ sur $(a,b)$ sauf pour $x=c$ ,alors $f(c)$ n’est ni maximum ni minimum de $f$

Tangente en un point:

$y-y_{0}=f'(x_{0})(x-x_{0})$

Normale en un point:

$y-y_{0}=-\frac{1}{f'(x_{0})}(x-x_{0})$

Points d’Inflection

Si $f'(x_{3})$ existe et $f''(x)$ change de signe au point d’abscisse $x=x_{3}$ ,le point $(x_{3}, f(x_{3}))$ est un point d’inflection pour le graphe de $f(x)$ . Si $f''(x_{3})$ existe au point d’inflection, alors $f''(x_{3})=0$