
The Bretscheiner’s formula helps find the area of a non-cyclic quadrilateral, that cannot be inscribed in a circle,
using only side lengths and possibly one angle measure or one diagonal length.
After the Bretschneider’s formula, we’ll simplify the quadrilateral to make it cyclic. We’ll get the Brahmagupta’s formula.
With the cyclic quadrilateral the product of the diagonals ![]() and
and ![]() is
is ![]() and opposite angles are supplementary.
and opposite angles are supplementary.
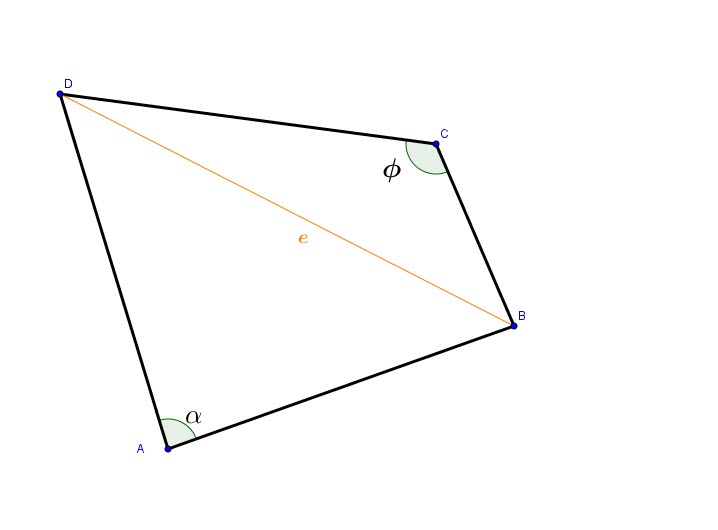
Let ![]() be area.
be area.
From the figure, we notice ![]()
![]()
![]()
Squaring both sides:
![]()
![]()
![]()
Now let’s check 2 values of diagonal ![]() :
:
![]()
![]()
![]()
![]()
![]()
Taking the square:
![]()
![]()
Adding ![]() and
and ![]() :
:
![]()
![]()
![]()
![]()
![]() Injected 2 in the last term.
Injected 2 in the last term.
![]()
To the same denominator and multiplying both sides by 4:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
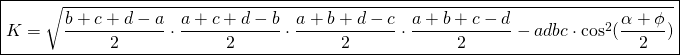
If we call the semi-perimeter ![]()
We have the final Bretscheiner’s formula:
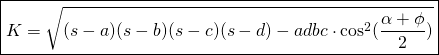
Brahmagupta’s formula
The steps remain the same but this time since the quadrilateral is ![]() we know that the two opposite angles are supplementary.
we know that the two opposite angles are supplementary.
![]()
We get from the Bretscheiner’s formula
![]()
Heron’s formula
The fourth side goes away and we get a triangle. From Brahmagupta’s formula:
![]()
In depth explanation:
From Al-Kashi to Bretshneider via Heron and Brahmagupta, we are going to go through some of their work:
Al-kashi is simply the Law of Cosines:
Law of cosines:
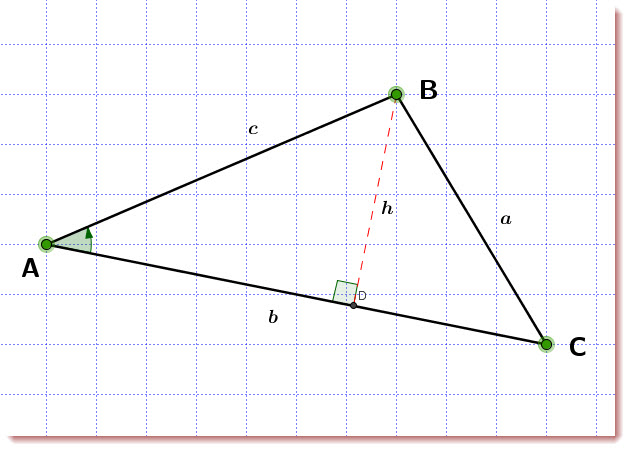
From what we know:
![]()
We have two right triangles: ![]() and
and ![]()
Using the Pythagorean Theorem:
![]()
Also:
![]()
![]()
But :
![]()
This means:
![]()
![]()
![]()
![]()
![]()
We know from above: ![]()
![]()
Finally we have the ![]() :
:
![]()
![]()
![]()
Heron Formula:
This one is widely used. We use it when we have only sides and we want to find the Area of the triangle
Let![]() be area and
be area and ![]() the semi-perimeter.
the semi-perimeter.
![]() .
.
We should remember this because we’ll need it in the following paragraphs.
![]()
![]()
But we know that:
![]()
![]()
![]()
![]()
![]()
This is a difference of squares, we can factor:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This is the Heron formula:
![]()
The Bretschneider formula:

We will demonstrate the following forms of the Area ![]() per BRETSCHNEIDER
per BRETSCHNEIDER
![]()
![]()
![]()
We split the diagonal ![]() into
into ![]() and
and ![]()
The same way for ![]() :
: ![]() and
and ![]()
We express the area of the four triangles:
![]()
![]()
![]()
![]()
Now we add all four areas:
![]()
![]()
After simplication:
![]()
The first form:
![]()
Now the second form:
From the figure:
![]()
![]()
![]()
![]()
We expand and replace terms in ![]() by
by ![]()
![]()
Now we move to the ![]()
![]()
![]()
We expand and replace terms in ![]() by
by ![]()
![]()
Now we move to the ![]()
![]()
![]()
![]()
Let’s add as follows:
![]()
![]()
![]()
After simplification we get:
![]()
But:
![]()
We plug in ![]()
![]()
Second Form:
![]()
Third form:
From the sequences above:
![]()
But: ![]()
![]()
![]()
![]()
![]()
This is the actual BRETSCHNEIDER formula:
![]()
According to wiki, the following work is credited to COOLIDGE in 1939:
Let ![]() be area.
be area.
From the figure, we notice ![]()
![]()
![]()
Squaring both sides:
![]()
![]()
![]()
Now let’s check 2 values of diagonal ![]() :
:
![]()
![]()
![]()
![]()
![]()
Taking the square:
![]()
![]()
Adding ![]() and
and ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]() Injected 2 in the last term.
Injected 2 in the last term.
![]()
To the same denominator and multiplying both sides by 4:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
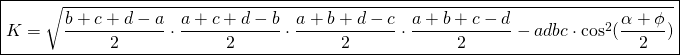
If we call the semi-perimeter ![]()
We have the final COOLIDGE formula:
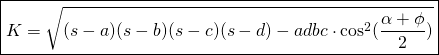
External links:
http://www.planetmath.org


Be the first to comment