Promoting the study of Geometry

Joining forces with institut-delbol.com, mouctar.org is publishing the first challenge.

The callenge second part is now solved. No more answers will be accepted. There was no winner for this challenge.

The following is the Algebraic method.

PROBLEM 2: THE TRAPEZOID

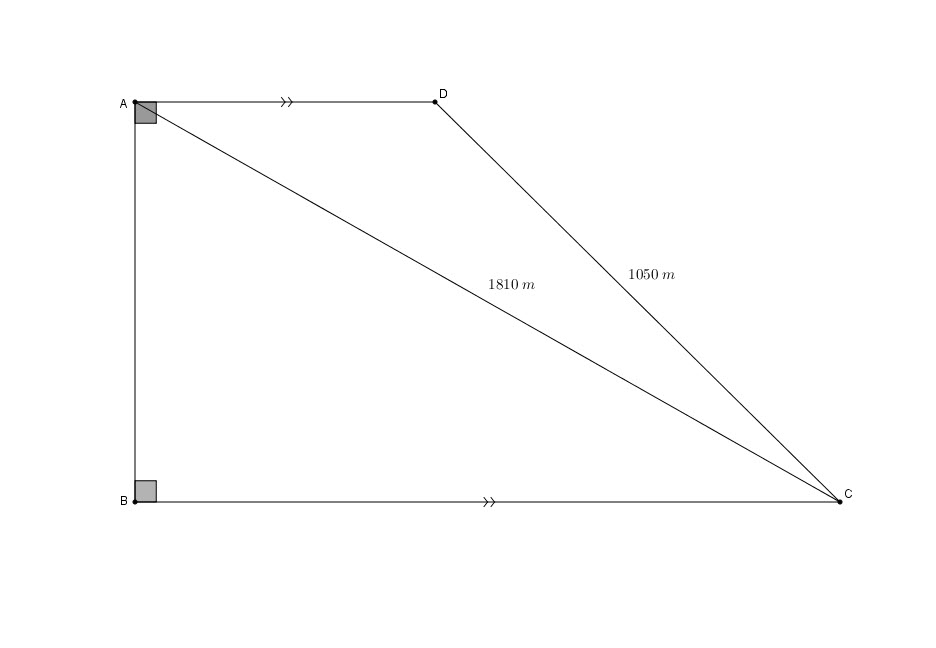
An agency is assigning the area bounded by figure $ABCD$ to a city population.

Each member will receive an equal area of a land plot.

Calculations have shown that out of the 5160 members of the population, 2000 will receive their plots from the area covered by triangle $ADC$

The remaining people will be assigned plots from $ABC$ , (See graph).

$DC=1050\;m$ and $AC=1810\:m$

1. Find the area of $ABCD$ $(30\; points)$

2. Verify the area of ADC using the Heron’s Formula $(10\; points)$

3. What is the area, in square meters, assigned to each person? $(10\; points)$

Click this link to read the pdf file

SOLUTION: METHOD BY ALGEBRA

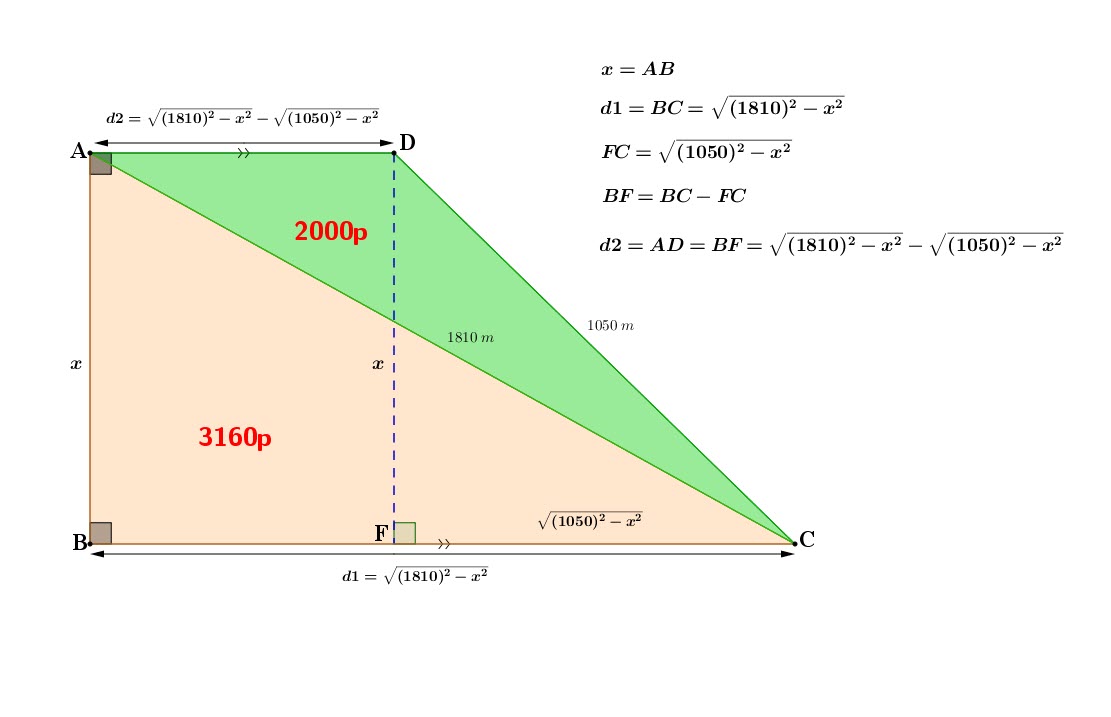
Let $AB=x$

$BC=d_{1}$

From the right triangle $\triangle ABC$ We have the hypothenuse $AC=1810$ .

We have:

$d_{1}=\sqrt{(1810)^{2}-x^{2}}$

We also have the right triangle $\triangle DFC$

$FC=\sqrt{(1050)^{2}-x^{2}}$

Another equality:

$AD=d_{2}=BF=BC-FC$

We can then say:

$d_{2}=\sqrt{(1810)^{2}-x^{2}}-\sqrt{(1050)^{2}-x^{2}}$

The area of $\triangle ABC$ contains 3160 plots of land out of 5160.

For $\triangle ABC$ :

$\mathcal{A} \triangle ABC$

The area of the $\triangle ABC=\frac{1}{2}\cdot x \cdot BC$

Area $\triangle ABC=\frac{1}{2}\cdot x \cdot d_{1}$

Area $\triangle ABC=\frac{1}{2}x \sqrt{(1810)^{2}-x^{2}}$

Now let’s look for the total area:

Area $\square ABCD=\square ABFD+\triangle DFC$

Area $\square ABFD$ :

Area $\square ABFD=x\cdot d_{2}$

We plugin:

Area $\square ABFD=x\cdot (\sqrt{(1810)^{2}-x^{2}}-\sqrt{(1050)^{2}-x^{2}})$

Area $\square ABFD=x\sqrt{(1810)^{2}-x^{2}}-x\sqrt{(1050)^{2}-x^{2}}$

For $\triangle DFC$ :

The area of the $\triangle DFC=\frac{1}{2}\cdot x \cdot FC$

Area $\triangle DFC=\frac{1}{2}\cdot x \cdot d_{1}$

Area $\triangle DFC=\frac{1}{2}\cdot x \cdot \sqrt{(1050)^{2}-x^{2}}$

TOTAL AREA :

Area $\square ABCD=\square ABFD+\triangle DFC$

We plugin:

Area $\displaystyle{\square ABCD=x\sqrt{(1810)^{2}-x^{2}}-x\sqrt{(1050)^{2}-x^{2}}+\frac{1}{2}x \sqrt{(1050)^{2}-x^{2}}}$

Area $\square ABCD=x\sqrt{(1810)^{2}-x^{2}}-\frac{1}{2}x \sqrt{(1050)^{2}-x^{2}}$

Comparing Areas:

Area $\triangle ABC=3160p$

Area $\square ABCD=5160p$

This yields:

$\frac{Area\; \square ABCD}{Area \; \triangle ABC}=\frac{5160p}{3160p}$

$Area \; \triangle ABC=\frac{3160p}{5160p}Area\; \square ABCD$

We simplify:

$Area \; \triangle ABC=\frac{79}{129}Area\; \square ABCD$

We plugin:

$\displaystyle{\frac{1}{2} x \sqrt{(1810)^{2}-x^{2}}=\frac{79}{129}(x\sqrt{(1810)^{2}-x^{2}}-\frac{1}{2}x \sqrt{(1050)^{2}-x^{2}})}$

We can write, for simplicity:

$\displaystyle{\frac{129}{158}x \sqrt{(1810)^{2}-x^{2}}=x\sqrt{(1810)^{2}-x^{2}}-\frac{1}{2}x \sqrt{(1050)^{2}-x^{2}}}$

We divide both sides by $x$

$\displaystyle{\frac{129}{158} \sqrt{(1810)^{2}-x^{2}}=\sqrt{(1810)^{2}-x^{2}}-\frac{1}{2} \sqrt{(1050)^{2}-x^{2}}}$

By moving we get:

$\frac{1}{2} \sqrt{(1050)^{2}-x^{2}}=(1-\frac{129}{158}) \sqrt{(1810)^{2}-x^{2}}$

$\frac{1}{2} \sqrt{(1050)^{2}-x^{2}}=\frac{29}{158} \sqrt{(1810)^{2}-x^{2}}$

Multiply both sides by 2:

$\sqrt{(1050)^{2}-x^{2}}=\frac{29}{79} \sqrt{(1810)^{2}-x^{2}}$

We can also write:

$\frac{0.79}{0.29}\sqrt{(1050)^{2}-x^{2}}=\sqrt{(1810)^{2}-x^{2}}$

Let $k=\frac{0.79}{0.29}$

We get:

$\sqrt{(1810)^{2}-x^{2}}=k\sqrt{(1050)^{2}-x^{2}}$

Let’s square both sides:

$(1810)^{2}-x^{2}=k^{2}((1050)^{2}-x^{2})$

$(1810)^{2}-x^{2}=k^{2}(1050)^{2}-k^{2}x^{2}$

$(k^{2}-1)x^{2}=k^{2}\cdot (1050)^{2}-(1810)^{2}$

$x^{2}=\frac{k^{2}\cdot (1050)^{2}-(1810)^{2}}{k^{2}-1}$

$x=\sqrt{\frac{k^{2}\cdot (1050)^{2}-(1810)^{2}}{k^{2}-1}}$

We plugin the values:

$\displaystyle{x=\sqrt{\frac{(\frac{0.79}{0.29})^{2}\cdot (1050)^{2}-(1810)^{2}}{(\frac{0.79}{0.29})^{2}-1}}}$

$x=874.0605963$

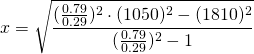
Rounded Value here:

$x=874\; m$

Areas:

The other sides:

$d_{1}=\sqrt{(1810)^{2}-x^{2}}$

$d_{1}=\sqrt{(1810)^{2}-(874.0605963)^{2}}$

$d_{1}=1584.966269$

$d_{1}=1585\;m$

$d_{2}=\sqrt{(1810)^{2}-x^{2}}-\sqrt{(1050)^{2}-x^{2}}$

$\displaystyle{d_{2}=\sqrt{(1810)^{2}-(874.0605963)^{2}}-\sqrt{(1050)^{2}-(874.0605963)^{2}}}$

$d_{2}=1003.143208$

$d_{2}=1003\;m$

Area $\triangle ABC=\frac{1}{2}x\cdot d_{1}$

Area $\triangle ABC=\frac{1}{2}\times 874.0605963\times 1584.966269$

Area $\triangle ABC=692678.2811$

Rounding:

Area $\triangle ABC=692678 \;m^{2}$

$TOTAL\; AREA:$

Trapezoid:

$AREA\; \square ABCD=\frac{d_{1}+d_{2}}{2}\cdot x$

$AREA\; \square ABCD=\frac{1584.966269+1003.143208}{2}\times 874.0605963$

$AREA\; \square ABCD=1131082.256$

$AREA\; ABCD=1131082\;m^{2}$

$SIZE\; OF \;THE\; PLOT:\; 5160\; plots$

$AREA \;PLOT=\frac{1131082}{5160}$

$AREA \;PLOT=219\;m^{2}$

Using the heron Formula for Area ADC

The sides are: $1050$ , $1810$ , $1003.143208$

Calculating $s$ :

$s=\frac{1050+1810+1003.143208}{2}$

$s=1931.571604$

$s-1050=1931.571604-1050=881.571604$

$s-1810=1931.571604-1810=121.571604$

$s-1003.143208=1931.571604-1003.143208=928.428396$

Area $\triangle ADC=\sqrt{1931.571604 \times 881.571604 \times 121.571604 \times 928.428396 }$

Area $\triangle ADC=438403.9751$

ROUNDING:

Area $\triangle ADC=438404\; m^{2}$

Post Views: 83

Challenge 1 Spring of 2017: Trapezoid Solution Algebra

Promoting the study of Geometry

PROBLEM 2: THE TRAPEZOID

SOLUTION: METHOD BY ALGEBRA

Using the heron Formula for Area ADC

Be the first to comment

Leave a Reply Cancel reply