geometry-lesson-5-circle-essentials

Circle Essentials

A circle is a set of all points in a plane that are equidistant to a given point called center. We have introduced the unit circle in trigonometry.

-The is a segment that joins the center of the circle to a given point on the circle. In the following diagram, we have segment OF representing a radius.

All of a circle are congruent.

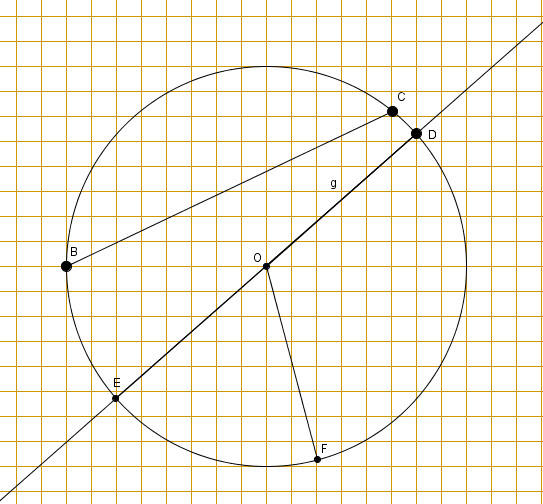
-Any line segment joining two points of a circle is called a of the circle. is a chord.

-A is a line that contains a chord. Line is a secant and contains .

-A of the circle is a chord passing through the center of the circle.  si a chord passing through center . It is a diameter.

Congruent circles have congruent radii.

-Concentric circles are coplanar circles having a common center.

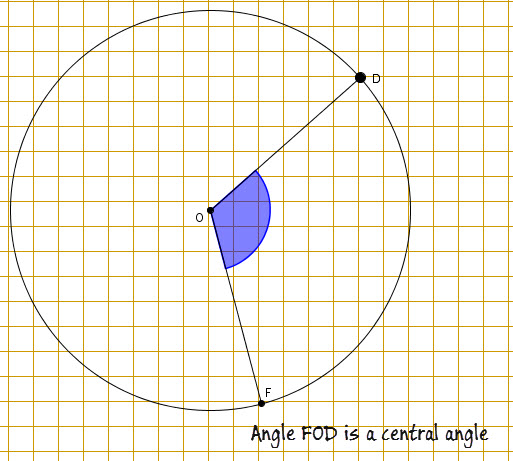
-An angle having its vertex at the center of the circle is called a .

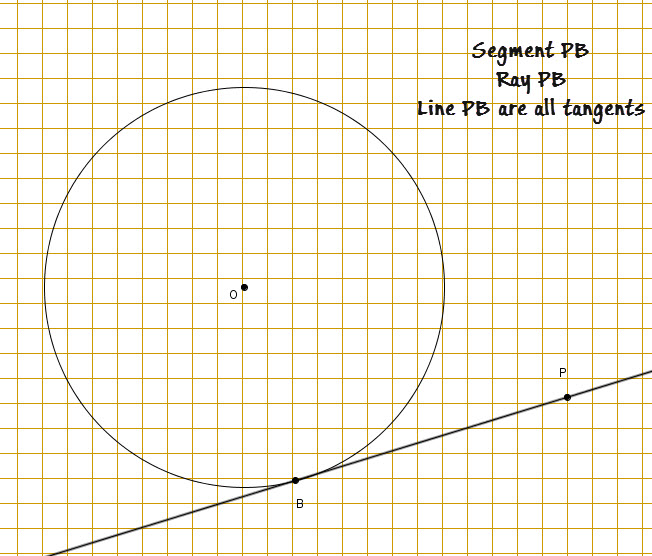
A is a line in the plane of a circle that intersects the circle in exactly one point, called the .

In the following figure, , and are called tangent segment, tangent line and tangent ray.

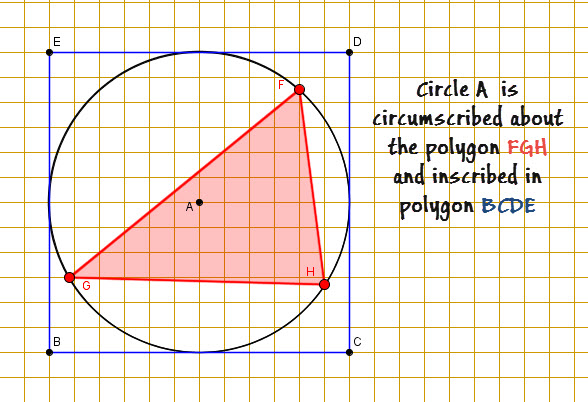
Inscribed and circumscribed circles:

When each side of a polygon is a tangent to a circle, the circle is said to be in the polygon.

By the same token, the polygon is said to .

Conversely, a polygon is inscribed in a circle and the circle is circumscribed about the polygon when each vertex of the polygon lies on the circle.

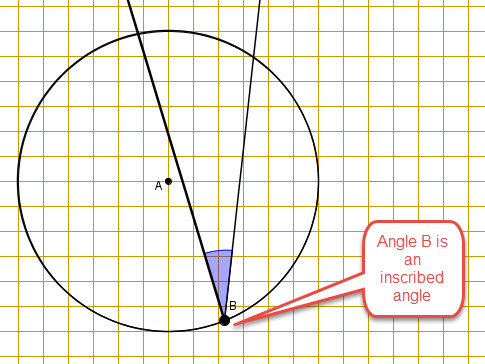
Inscribed angle:

An inscribed angle is an angle with the vertex on the circle and the sides containing chords of that circle.

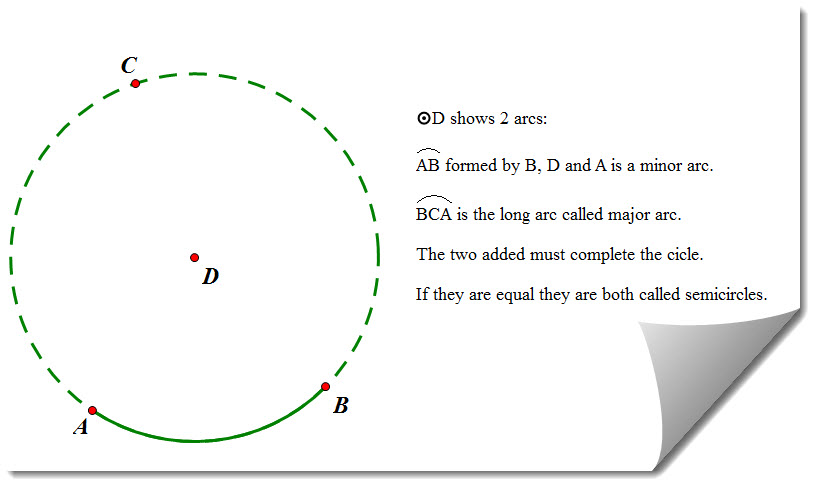
 Major and minor arcs

The major and minor arcs added complete the circumference of the circle. If they are equal, they are called semicircles.

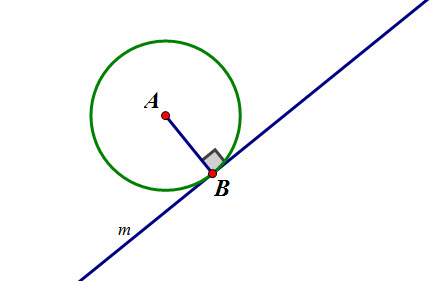
 Tangents: Theorems and postulates

Theorem:

If a line is tangent to a circle, then the line is perpendicular to the radius drawn to the point of tangency

Note:

We can prove that by remembering that the shortest distance between a point and a line is on the perpendicular to that line.

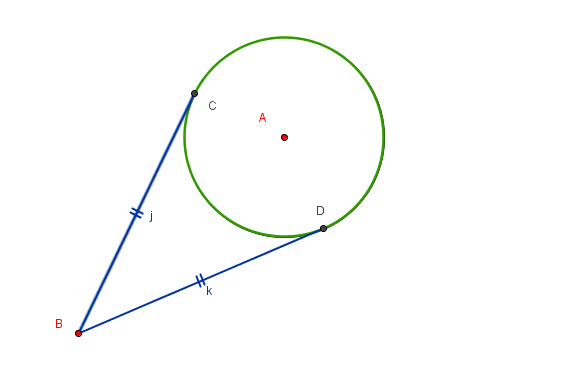
Corollary:

Tangents to a circle from a point are congruent.

Theorem:

If a line in the plane of a circle is perpendicular to a radius at its outer endpoint, then the line is tangent to the circle

Arcs and angles: Theorems and postulates

Postulate: Arc addition

The measure of the arc formed by two adjacent arcs is the sum of the measures of these two arcs.

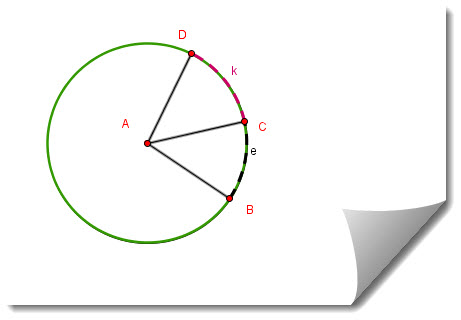
Theorem:

In the same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are congruent.

Arcs and Chords: Theorems and postulates:

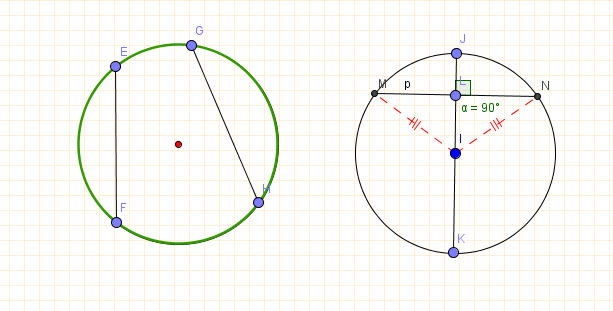
Theorem:

In the same circle or in congruent circles, the congruent arcs have congruent chords and congruent chords have congruent arcs.

Theorem:

If a diameter or radius is perpendicular to a chord, then it bisects that chord and its arc.

Theorem:

In the same circle or in congruent circles, if two chords are equally distant from the center, then they are congruent and vice versa.

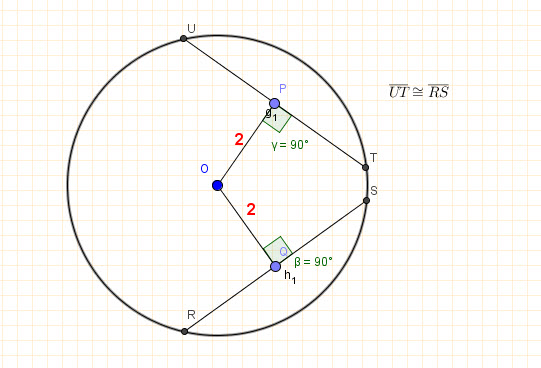
Inscribed angles: Theorems and postulates

Theorem:

The measure of an inscribed angle is equal to the half of the measure of its intercepted arc.

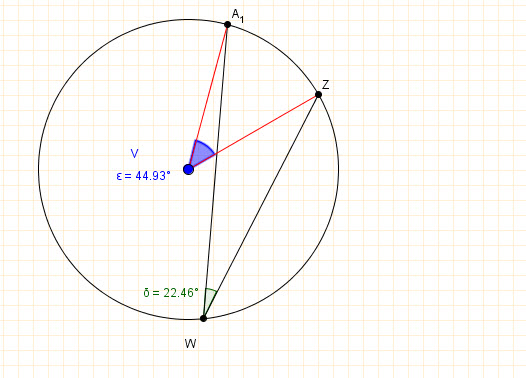
Corollary:

1.If two inscribed angles intercept the same arc, then the angles are congruent

2.An angle inscribed in a semicircle is a right angle

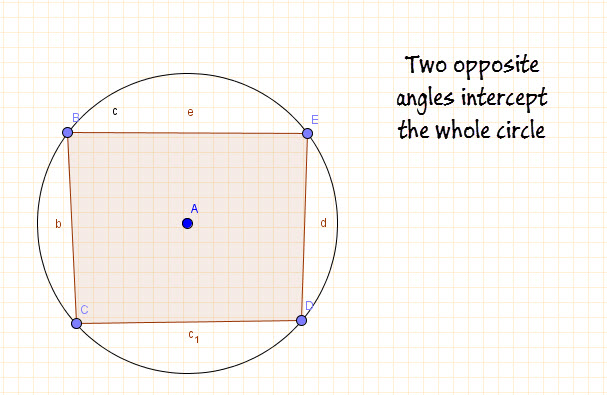
3.If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary

Theorem:

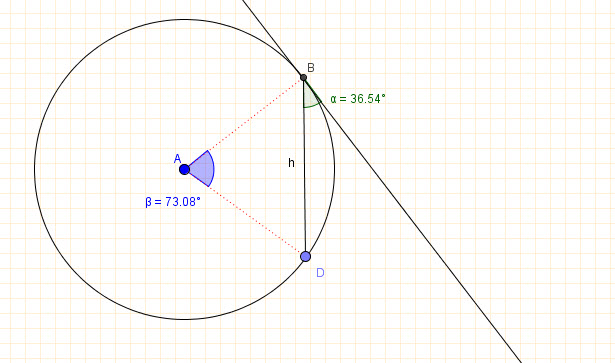
The measure of an angle formed by a chord and a tangent is equal to half the measure of the intercepted arc.

Theorem:

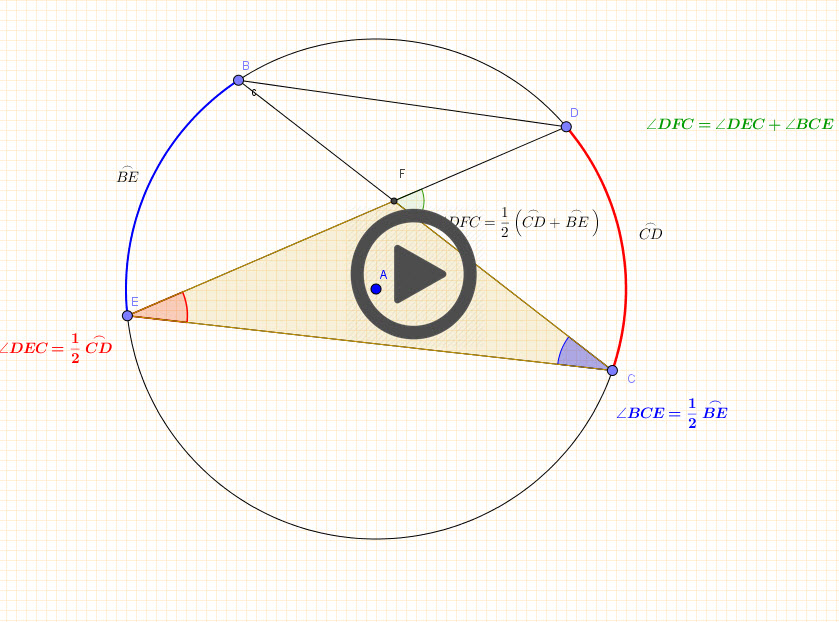
The measure of an angle formed by two chords that intersect inside a circle is equal to half the sum of the measures of the intercepted arcs

Theorem:

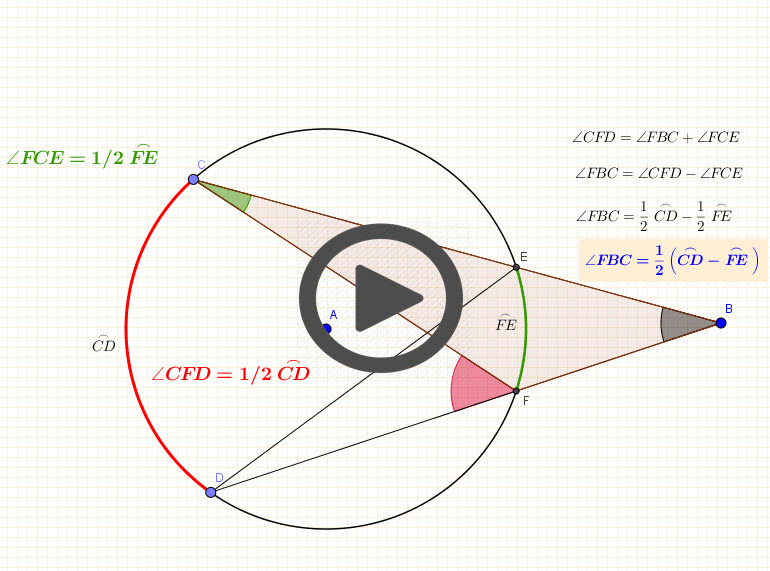
The measure of an angle formed by two secants, two tangents, or a secant and a tangent drawn from a point outside a circle is equal to half the difference of the measures of the intercepted arcs

Circles and lengths of segments

Theorem:

When two chords intersect inside a circle, the product of the segments of one chord equals the product of the segments of the other chord.

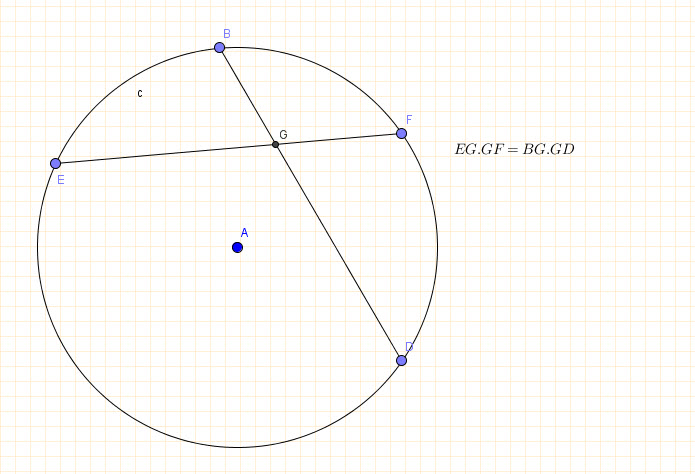
Theorem:

When two secant segments are drawn to a circle from an external point, the product of one secant segment and its external segment equals the product of the other secant segment and its external segment.

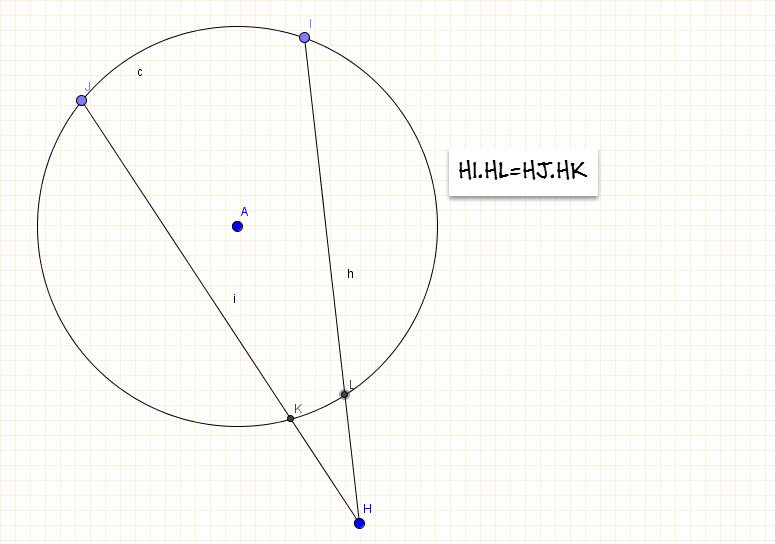
Theorem:

When a secant segment and a tangent segment are drawn to a circle from an external point, the product of the secant segment and its external segment is equal to the square of the tangent segment.

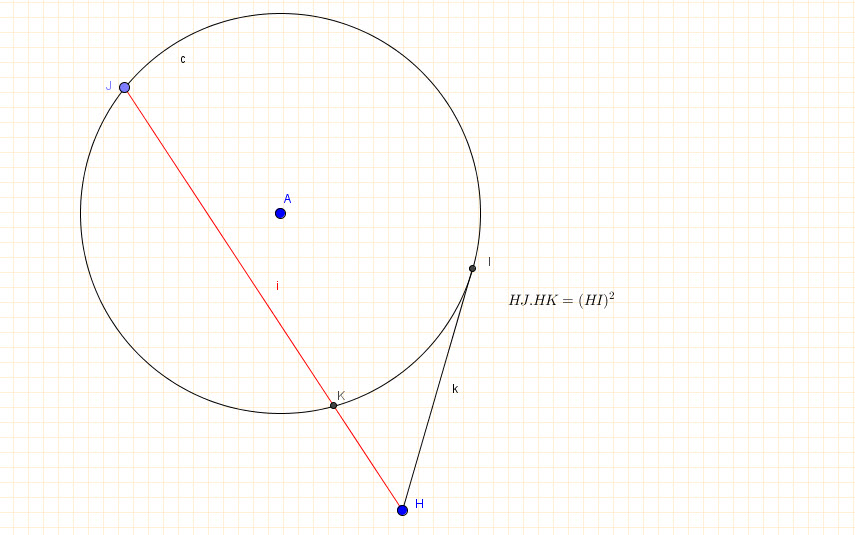
Construction works