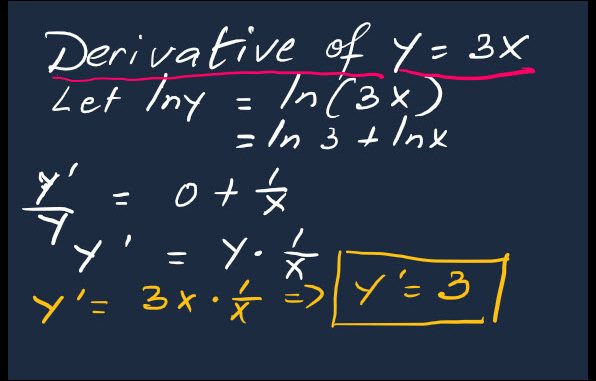
Derivatives

After a brief coverage of the $limits$ calculations, we can now start diving into the heart of the differentiation calculations.

In geometry, when we calculate the slope of the tangent of given graph, we get the rate of change at the tangency point.

We are going to use that information and define our derivatives.

Let’s take a point on a function : $(x, f(x))$

If $a$ is the value of $x$ at the tangency point, we can write the value of the slope $m$ as follows :

$m=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

We’ll use to define the derivative:

The $derivative$ of a function $f$ noted $f'$ can be written:

$f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

as long as the limit exists.

We may also use the following notation:

$\frac{dy}{dx}=f'(x)$

If we let $y=f(x)$

And we add a change to the value of $x$ , changing it to $x+\delta x$ , we will cause $y$ to change to $y+ \delta y$

This means:

$y+\delta y=f(x+\delta x)$

Pairing the following equations and subtracting:

$\begin{cases}y=f(x)\\y+\delta y=f(x+\delta x) \end{cases}$

We get :

$\delta y=f(x+\delta x)-f(x)$

If we divide by $\delta x$ and making $\delta x$ very close to $0$

We have the corresponding differential of $f(x)$

$\frac{dy}{dx}=\lim_{\delta x \to 0}\frac{\delta y}{\delta x}=\lim_{\delta x \to 0}\frac{f(x+\delta x)-f(x)}{\delta x}$

This is the derivative of the function.

EXAMPLE

Differentiate $f(x)=x^{2}$

(1) $\begin{equation*} \begin{split} f'(x)&=\lim_{h \to 0}\frac{(x+h)^{2}-x^{2}}{h}\\&= \lim_{h \to 0}\frac{x^{2}+2xh+h^{2}-x^{2}}{h}\\ &=\lim_{h \to 0}\frac{2xh+h^{2}}{h}\\&=\lim_{h \to 0}(2x+h)\\&=2x \end{split} \end{equation*}$

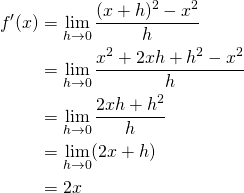
Problem:

Given

$f(x)=\ln x$

Find:

$f'(x)$

Solution:

$y=\ln x$

(2) $\begin{equation*} \begin{split} \frac{dy}{dx}&=\lim_{\delta x \to 0}\frac{\ln (x+\delta x)- \ln x}{\delta x}\\ &=\lim_{\delta x \to 0}\frac{1}{\delta x}\ln (\frac{x+\delta x}{\delta x})\\ &=\lim_{\delta x \to 0}\frac{1}{\delta x} \cdot \frac{x}{x} \ln (1+\frac{x}{\delta x})\\ &= \lim_{\delta x \to 0}\frac{x}{\delta x} \cdot \frac{1}{x} \ln (1+\frac{x}{\delta x}) \\ &=\lim_{\delta x \to 0}\frac{1}{x} \ln (1+\frac{x}{\delta x})^{\frac{x}{\delta x}} \end{split} \end{equation*}$

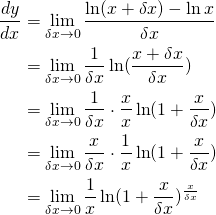
But we know that:

For values of $x\geq 0$ when $\delta x \rightarrow 0$ , $\frac{x}{\delta x} \rightarrow \infty$

Combining with the definition of $e$ in our logarithms definition:

$\lim_{\delta x \to 0} \ln (1+\frac{x}{\delta x})^{\frac{x}{\delta x}}=\ln e=1$

Finally:

$\frac{dy}{dx}=\frac{1}{x}\cdot 1$

We write:

$(\ln x)'=\frac{1}{x}$

Table of fundamental derivatives

No.	Function	Derivative
$01.$	$C$	$0$
$02.$	$x$	$1$
$03.$	$ax+b$	$a$
$04.$	$x^{n}$	$nx^{n-1}$
$05.$	$x^{-n}$	$-\frac{n}{x^{n+1}}$
$06.$	$\frac{1}{x}$	$-\frac{1}{x^{2}}$
$07.$	$\sqrt{x}$	$\frac{1}{2\sqrt{x}}$
$08.$	$\sqrt[n]{x}$	$\frac{1}{n\sqrt[n]{x-1}}$
$09.$	$\ln x$	$\frac{1}{x}$
$10.$	$\log_{a}x$	$\frac{1}{x \ln a}$
$11.$	$a^{x}$	$a^{x} \ln a$
$12.$	$e^{x}$	$e^{x}$
$13.$	$u$	$u'$
$14.$	$u^{n}$	$nu^{n-1}u'$
$15.$	$u+v$	$u'+v'$
$16.$	$u-v$	$u'-v'$
$17.$	$uv$	$u'v+uv'$
$18.$	$\frac{u}{v}$	$\frac{u'v-uv'}{v^{2}}$
$19.$	$\frac{u}{C}$	$\frac{1}{C}u'$
$20.$	$Cu$	$Cu'$
$21.$	$\sin x$	$\cos x$
$22.$	$\cos x$	$-\sin x$
$23.$	$\tan x$	$\frac{1}{\cos^{2}x}$ or $\sec^{2}x$
$24.$	$\cot x$	$-\frac{1}{\sin^{2}x}$ or $-\csc^{2}x$
$25.$	$\sec x$	$\tan x \cdot \sec x$
$26.$	$\csc x$	$-\cot x \cdot \csc x$
$27.$	$\sin^{-1}x$	$\frac{1}{\sqrt{1-x^{2}}}$
$28.$	$\cos^{-1}x$	$-\frac{1}{\sqrt{1-x^{2}}}$
$29.$	$\tan^{-1}x$	$\frac{1}{1+x^{2}}$
$30.$	$\cot^{-1}x$	$-\frac{1}{1+x^{2}}$
$31.$	$\sec^{-1}x$	$\frac{1}{\|x\|\sqrt{x^{2}-1}}$
$32.$	$\csc^{-1}x$	$-\frac{1}{\|x\|\sqrt{x^{2}-1}}$
$33.$	$\sinh x$	$\cosh x$
$34.$	$\cosh x$	$\sinh x$
$35.$	$\tanh x$	$\frac{1}{\cosh^{2}x}$
$36.$	$\coth x$	$-\frac{1}{\sinh^{2}x}$
$37.$	$\sinh^{-1}x$	$\frac{1}{\sqrt{x^{2}+1}}$
$38.$	$\cosh^{-1}x$	$-\frac{1}{\sqrt{x^{2}-1}}$
$39.$	$\tanh^{-1}x$	$\frac{1}{1-x^{2}}$
$40.$	$\coth^{-1}x$	$-\frac{1}{x^{2}-1}$
$41.$	$\ln u$	$\frac{u'}{u}$
$42.$	$\cos u$	$-u'\sin u$
$43.$	$\sin u$	$u'\cos u$
$44.$	$e^{u} x$	$u'e^{u}$
$45.$	$\tan u$	$\frac{u'}{\cos^{2}u}$
$46.$	$\cot u$	$\frac{u'}{\sin^{2}u}$
$47.$	$\sin^{-1}u$	$\frac{u'}{\sqrt{1-u^{2}}}$
$48.$	$\cos^{-1}u$	$-\frac{u'}{\sqrt{1-u^{2}}}$
$49.$	$\tan^{-1}u$	$\frac{u'}{1+u^{2}}$
$50.$	$\cot^{-1}u$	$-\frac{u'}{1+u^{2}}$
$51.$	$\sec^{-1}u$	$\frac{u'}{\|u\|\sqrt{u^{2}-1}}$
$52.$	$\csc^{-1}u$	$-\frac{u'}{\|u\|\sqrt{u^{2}-1}}$