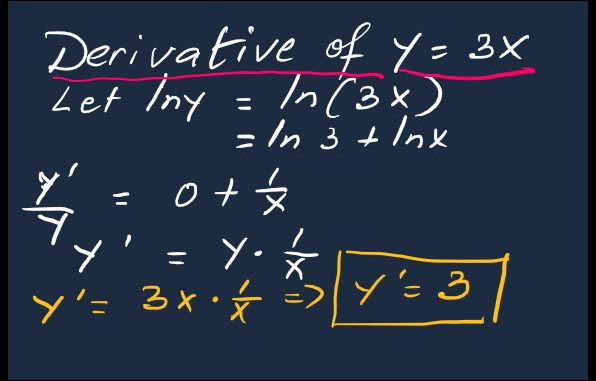
Dérivée

Dérivée

Après le petit aperçu sur les calculs de $limites$ , nous pouvons maintenant aborder les calculs des dérivées.

En géométrie, quand on calcule le coefficient directeur d’une tangente à une courbe donnée, la vitesse de changement ou differentielle en ce point.

Nous utiliserons cette définition dans ce qui suit

Soit un point sur la courbe d’une fonction : $(x, f(x))$

Si $a$ est la valeur de $x$ au point de tangence, nous pourrons noter la valeur du coefficient directeur $m$ comme suit :

$m=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

Ce qui nous permet de définir la dérivée.

La $dérivée$ d’une fonction $f$ notée $f'$ peut s’écrire:

$f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Si la limite existe.

On peut aussi noter:

$\frac{dy}{dx}=f'(x)$

Si on désigne $y=f(x)$

Et on ajoute une variation à la valeur de $x$ , pour obtenir $x+\delta x$ , nous engendrons une variation de $y$ qui devient $y+ \delta y$

Ce qui signifie:

$y+\delta y=f(x+\delta x)$

En combinant ces deux équations et en effectuant la soustraction:

$\begin{cases}y=f(x)\\y+\delta y=f(x+\delta x) \end{cases}$

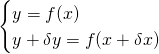
On obtient :

$\delta y=f(x+\delta x)-f(x)$

En divisant par $\delta x$ et rendant $\delta x$ infiniment proche de $0$

Nous avons la différentielle correspondante de $f(x)$

$\frac{dy}{dx}=\lim_{\delta x \to 0}\frac{\delta y}{\delta x}=\lim_{\delta x \to 0}\frac{f(x+\delta x)-f(x)}{\delta x}$

C’est la dérivée de la fonction.

EXEMPLE

Trouver la dérivée de $f(x)=x^{2}$

(1) $\begin{equation*} \begin{split} f'(x)&=\lim_{h \to 0}\frac{(x+h)^{2}-x^{2}}{h}\\ &=\lim_{h \to 0}\frac{x^{2}+2xh+h^{2}-x^{2}}{h}\\ &=\lim_{h \to 0}\frac{2xh+h^{2}}{h}\\ &=\lim_{h \to 0}(2x+h)\\&=2x \end{split} \end{equation*}$

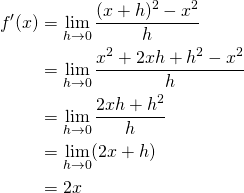
Problème:

Soit

$f(x)=\ln x$

Trouver:

$f'(x)$

Solution:

$y=\ln x$

(2) $\begin{equation*} \begin{split} \frac{dy}{dx}&=\lim_{\delta x \to 0}\frac{\ln (x+\delta x)- \ln x}{\delta x}\\ &=\lim_{\delta x \to 0}\frac{1}{\delta x}\ln (\frac{x+\delta x}{\delta x})\\ &=\lim_{\delta x \to 0}\frac{1}{\delta x} \cdot \frac{x}{x} \ln (1+\frac{x}{\delta x})\\ &= \lim_{\delta x \to 0}\frac{x}{\delta x} \cdot \frac{1}{x} \ln (1+\frac{x}{\delta x}) \\ &=\lim_{\delta x \to 0}\frac{1}{x} \ln (1+\frac{x}{\delta x})^{\frac{x}{\delta x}} \end{split} \end{equation*}$

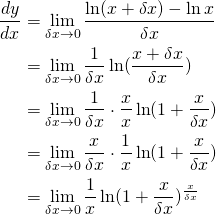
Mais nous savons que:

Pour des valeurs de $x\geq 0$ quand $\delta x \rightarrow 0$ , $\frac{x}{\delta x} \rightarrow \infty$

Combinant la définition de $e$ dans la définition des logarithmes:

$\lim_{\delta x \to 0} \ln (1+\frac{x}{\delta x})^{\frac{x}{\delta x}}=\ln e=1$

Finalement:

$\frac{dy}{dx}=\frac{1}{x}\cdot 1$

On écrit:

$(\ln x)'=\frac{1}{x}$

Table de quelques dérivées

No.	Function	Derivative
$01.$	$C$	$0$
$02.$	$x$	$1$
$03.$	$ax+b$	$a$
$04.$	$x^{n}$	$nx^{n-1}$
$05.$	$x^{-n}$	$-\frac{n}{x^{n+1}}$
$06.$	$\frac{1}{x}$	$-\frac{1}{x^{2}}$
$07.$	$\sqrt{x}$	$\frac{1}{2\sqrt{x}}$
$08.$	$\sqrt[n]{x}$	$\frac{1}{n\sqrt[n]{x-1}}$
$09.$	$\ln x$	$\frac{1}{x}$
$10.$	$\log_{a}x$	$\frac{1}{x \ln a}$
$11.$	$a^{x}$	$a^{x} \ln a$
$12.$	$e^{x}$	$e^{x}$
$13.$	$u$	$u'$
$14.$	$u^{n}$	$nu^{n-1}u'$
$15.$	$u+v$	$u'+v'$
$16.$	$u-v$	$u'-v'$
$17.$	$uv$	$u'v+uv'$
$18.$	$\frac{u}{v}$	$\frac{u'v-uv'}{v^{2}}$
$19.$	$\frac{u}{C}$	$\frac{1}{C}u'$
$20.$	$Cu$	$Cu'$
$21.$	$\sin x$	$\cos x$
$22.$	$\cos x$	$-\sin x$
$23.$	$\tan x$	$\frac{1}{\cos^{2}x}$ or $\sec^{2}x$
$24.$	$\cot x$	$-\frac{1}{\sin^{2}x}$ or $-\csc^{2}x$
$25.$	$\sec x$	$\tan x \cdot \sec x$
$26.$	$\csc x$	$-\cot x \cdot \csc x$
$27.$	$\sin^{-1}x$	$\frac{1}{\sqrt{1-x^{2}}}$
$28.$	$\cos^{-1}x$	$-\frac{1}{\sqrt{1-x^{2}}}$
$29.$	$\tan^{-1}x$	$\frac{1}{1+x^{2}}$
$30.$	$\cot^{-1}x$	$-\frac{1}{1+x^{2}}$
$31.$	$\sec^{-1}x$	$\frac{1}{\|x\|\sqrt{x^{2}-1}}$
$32.$	$\csc^{-1}x$	$-\frac{1}{\|x\|\sqrt{x^{2}-1}}$
$33.$	$\sinh x$	$\cosh x$
$34.$	$\cosh x$	$\sinh x$
$35.$	$\tanh x$	$\frac{1}{\cosh^{2}x}$
$36.$	$\coth x$	$-\frac{1}{\sinh^{2}x}$
$37.$	$\sinh^{-1}x$	$\frac{1}{\sqrt{x^{2}+1}}$
$38.$	$\cosh^{-1}x$	$-\frac{1}{\sqrt{x^{2}-1}}$
$39.$	$\tanh^{-1}x$	$\frac{1}{1-x^{2}}$
$40.$	$\coth^{-1}x$	$-\frac{1}{x^{2}-1}$
$41.$	$\ln u$	$\frac{u'}{u}$
$42.$	$\cos u$	$-u'\sin u$
$43.$	$\sin u$	$u'\cos u$
$44.$	$e^{u} x$	$u'e^{u}$
$45.$	$\tan u$	$\frac{u'}{\cos^{2}u}$
$46.$	$\cot u$	$\frac{u'}{\sin^{2}u}$
$47.$	$\sin^{-1}u$	$\frac{u'}{\sqrt{1-u^{2}}}$
$48.$	$\cos^{-1}u$	$-\frac{u'}{\sqrt{1-u^{2}}}$
$49.$	$\tan^{-1}u$	$\frac{u'}{1+u^{2}}$
$50.$	$\cot^{-1}u$	$-\frac{u'}{1+u^{2}}$
$51.$	$\sec^{-1}u$	$\frac{u'}{\|u\|\sqrt{u^{2}-1}}$
$52.$	$\csc^{-1}u$	$-\frac{u'}{\|u\|\sqrt{u^{2}-1}}$