Distance between a line and a point
In many cases, we will need to find the shortest distance between a line a point.
This distance is on the perpendicular of the line. This means that we need to get the intersection point and calculate the distance between the two points.
For instance, if the point is ![]() and the lines intersect at
and the lines intersect at ![]() , we need the distance
, we need the distance ![]() .
.
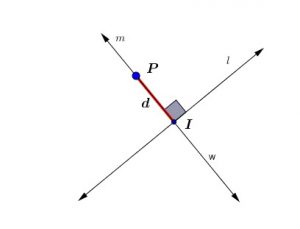
Distance between point ![]() and line
and line ![]()
The point is ![]() is on the line perpendicular to the given line
is on the line perpendicular to the given line ![]()
The product of the slopes is ![]()
We start by putting ![]() in the slope-intercept form
in the slope-intercept form
![]()
![]()
![]()
That means:![]()
Now we have to find ![]() from
from ![]() :
:
![]()
![]()
![]()
![]() after we multiply both sides by
after we multiply both sides by ![]()
The perpendicular is a line passing through ![]() with a slope of
with a slope of ![]()
We get for the perpendicular:
![]()
![]()
When the two lines meet, they have corresponding coordinates ![]() and
and ![]() .
.
We get:
![]()
![]()
![]()
![]()
![]()
Now we multiply both sides by ![]()
![]()
Dividing by ![]()
To find ![]() we use any of the two lines and plug in
we use any of the two lines and plug in ![]() expression.
expression.
From:
![]()
We get
(1) 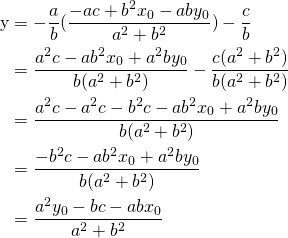
Finally:
Now we have the two points, all we need is to calculate the distance:
![]()
![]()
Distance ![]() :
:
(2) 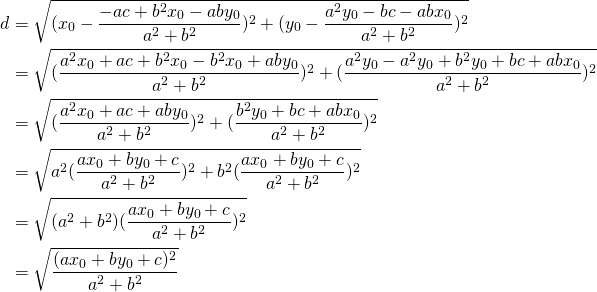
Finally:
![]()

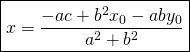
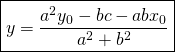
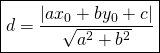

Be the first to comment