Distance entre une droite et un point

Dans beaucoup de cas, nous aurons besoin de trouver la plus courte distance entre une droite et un point extérieur à cette droite.

Cette distance n’est autre que la longueur d’un segement contenu dans une autre droite perpendiculaire à la première. Ce segment part du point et finit à l’intersection des deux droites.

Par exemple, si le point est $P$ et les deux droites se coupent en $I$ , nous chercherons la distance $PI$ .

Distance entre le point $P(x_0,y_0)$ et la droite $ax+by+c=0$

Le point $P(x_0,y_0)$ se trouve sur la perpendiculaire à la droite $ax+by+c=0$

Nous avions vu que le produit des coefficients directeurs est de $m_1m_2=-1$

Mettons l’équation $ax+by+c=0$ sous la forme qui depicte le coefficient directeur.

$ax+by+c=0$
$by=-ax-c$
$y=-\frac{a}{b}x-\frac{c}{b}$

Ce qui signifie que:

$m_1=-\frac{a}{b}$

Nous devons maintenant trouver $m_2$ à partir de $m_1$ :

$m_1m_2=-1$

$-\frac{a}{b}m_2=-1$

$\frac{a}{b}m_2=1$

$m_2=\frac{b}{a}$ en multipliant les deux membres par $\frac{b}{a}$

La perpendiculaire est la ligne qui passe par $P(x_0,y_0)$ avec un coefficient directeur $m_2=\frac{b}{a}$

Nous obtenons pour la perpendiculaire:

$y-y_0=\frac{b}{a}(x-x_0)$

$y=\frac{b}{a}x-\frac{b}{a}x_0+y_0$

A l’intersection, les droites ont mêmes coordonnées $x$ et $y$ .

Nous aurons:

$y=-\frac{a}{b}x-\frac{c}{b}$

$y=\frac{b}{a}x-\frac{b}{a}x_0+y_0$

$-\frac{a}{b}x-\frac{c}{b}=\frac{b}{a}x-\frac{b}{a}x_0+y_0$

$x(\frac{b}{a}+\frac{a}{b})=-\frac{c}{b}+\frac{b}{a}x_0-y_0$

$x(\frac{a^{2}+b^{2}}{ab})=\frac{-ac+b^{2}x_0-aby_0}{ab}$

Multiplions les deux membres par $ab$

$x(a^{2}+b^{2})=-ac+b^{2}x_0-aby_0$

Divisons par $a^{2}+b^{2}$

$\boxed{x=\frac{-ac+b^{2}x_0-aby_0}{a^{2}+b^{2}}}$

Pour trouver $y$ nous remplacerons $x$ par sa valeur dans n’importe quelle droite.

De la droite:

$y=-\frac{a}{b}x-\frac{c}{b}$

Nous avons

(1) $\begin{equation*} \begin{split} $y&=-\frac{a}{b}(\frac{-ac+b^{2}x_0-aby_0}{a^{2}+b^{2}})-\frac{c}{b}\\ & =\frac{a^{2}c-ab^{2}x_0+a^{2}by_0}{b(a^{2}+b^{2})}-\frac{c(a^{2}+b^{2})}{b(a^{2}+b^{2})}\\ & =\frac{a^{2}c-a^{2}c-b^{2}c-ab^{2}x_0+a^{2}by_0}{b(a^{2}+b^{2})}\\ & =\frac{-b^{2}c-ab^{2}x_0+a^{2}by_0}{b(a^{2}+b^{2})}\\ &=\frac{a^{2}y_0-bc-abx_0}{a^{2}+b^{2}} \end{split} \end{equation*}$

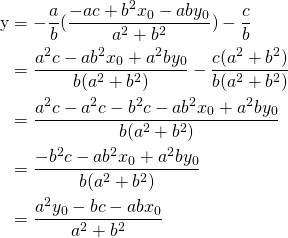
Finalement:

$\boxed{y=\frac{a^{2}y_0-bc-abx_0}{a^{2}+b^{2}}}$

Comme nous avons les deux points, on peut calculer la distance entre les deux points:

$P=(x_0, y_0)$

$I=(\frac{ac+b^{2}x_0-aby_0}{a^{2}+b^{2}},\frac{a^{2}y_0-bc-abx_0}{a^{2}+b^{2}})$

Distance $IP$ :

(2) $\begin{equation*} \begin{split} d&=\sqrt{(x_0-\frac{-ac+b^{2}x_0-aby_0}{a^{2}+b^{2}})^{2}+ (y_0-\frac{a^{2}y_0-bc-abx_0}{a^{2}+b^{2}})^{2}}\\ & =\sqrt{(\frac{a^{2}x_0+ac+b^{2}x_0-b^{2}x_0+aby_0}{a^{2}+b^{2}})^{2}+(\frac{a^{2}y_0-a^{2}y_0+b^{2}y_0+bc+abx_0}{a^{2}+b^{2}})^{2}}\\ & =\sqrt{(\frac{a^{2}x_0+ac+aby_0}{a^{2}+b^{2}})^{2}+(\frac{b^{2}y_0+bc+abx_0}{a^{2}+b^{2}})^{2}}\\ & =\sqrt{a^{2}(\frac{ax_0+by_0+c}{a^{2}+b^{2}})^{2}+b^{2}(\frac{ax_0+by_0+c}{a^{2}+b^{2}})^{2}}\\ & =\sqrt{(a^{2}+b^{2})(\frac{ax_0+by_0+c}{a^{2}+b^{2}})^{2}}\\ & =\sqrt{\frac{(ax_0+by_0+c)^{2}}{a^{2}+b^{2}}} \end{split} \end{equation*}$

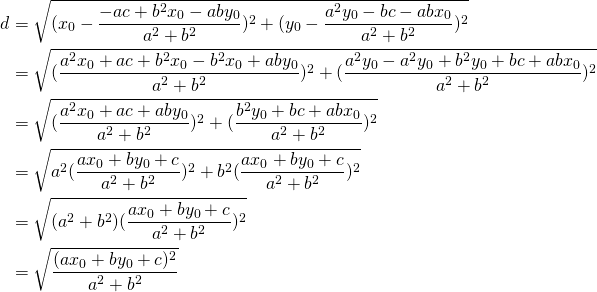
Finalement:

$\boxed{d=\frac{|ax_0+by_0+c|}{\sqrt{a^{2}+b^{2}}}}$

Post Views: 242

Distance entre une droite et un point

Distance entre une droite et un point

$\boxed{x=\frac{-ac+b^{2}x_0-aby_0}{a^{2}+b^{2}}}$

$\boxed{y=\frac{a^{2}y_0-bc-abx_0}{a^{2}+b^{2}}}$

$\boxed{d=\frac{|ax_0+by_0+c|}{\sqrt{a^{2}+b^{2}}}}$

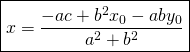
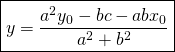
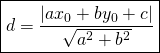
Be the first to comment

Leave a Reply Cancel reply