Equations Quadratiques, pages multiples
Une équation quadratique ou équation du second degré est de la forme:
Ces équations contiennent des polynômes du second degré, avec le carré comme plus grand exposant.
C’est très important d’identifier les valeurs des constantes ![]() ,
, ![]() et
et ![]() . La forme doit être écrite avec la forme ci-dessus.
. La forme doit être écrite avec la forme ci-dessus.
L’exposant ![]() doit être présent pour que l’équation soit considérée comme quadratique. Si l’équation est donnée sous une autre forme, nous pouvons re-écrire pour avoir
doit être présent pour que l’équation soit considérée comme quadratique. Si l’équation est donnée sous une autre forme, nous pouvons re-écrire pour avoir ![]() .
.
Exemple: ![]() On doit la re-écrire pour avoir une forme standard:
On doit la re-écrire pour avoir une forme standard:
![]()
![]()
En multipliant par ![]() pour avoir la forme connue:
pour avoir la forme connue: ![]()
Il faut noter que ![]() et
et ![]() peuvent être
peuvent être ![]() ,
, ![]() ou
ou ![]() .
.
1.Résoudre par mise en facteurs:
Nous avons utiliser ce type de facteurs par le passé. Maintenant nous verrons comment on avait ces facteurs.
Soit :
Résoudre par mise en facteurs.
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} ax^2+bx+c&=a(x^2+\frac{b}{a}x+\frac{c}{a})\\ &=a\left[{(x+\frac{b}{2a})}^2-{(\frac{b}{2a})}^2+\frac{c}{a}\right]\\ &=a\left[{(x+\frac{b}{2a})}^2-\frac{b^2}{4a^2}+\frac{4ac}{4a^2}\right]\\ &=a\left[{(x+\frac{b}{2a})}^2-\frac{(b^2-4ac)}{4a^2}\right]\\ &=a\left[{(x+\frac{b}{2a})}^2-{(\frac{\sqrt{b^2-4ac}}{2a})}^2\right] \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-01a28772e3a1b8a8e12a97c63a084779_l3.png)
Utilisons la formule de la différence des carrés:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} a\left[{\left(x+\frac{b}{2a}\right)}^2-{\left(\frac{\sqrt{b^2-4ac}}{2a}\right)}^2\right]&=a\left[\left(x+\frac{b}{2a}+\frac{\sqrt{b^2-4ac}}{2a}\right)\left(x+\frac{b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}\right)\right]\\ &=a\left[\left(x+\frac{b+\sqrt{b^2-4ac}}{2a}\right)\left(x+\frac{b-\sqrt{b^2-4ac}}{2a}\right)\right] \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-1276b788e0c70a4b5fcbf74dd0adee81_l3.png)
En retournant à l’équation:
![]()
Finalement nous avons:
De ![]()
![]()
Deux facteurs donnent toujours la solution.
Les deux valeurs de ![]() sont:
sont:
2.D’autres méthodes:
Il se pourrait que les racines soient des entiers relatifs facile à trouver. Nous utilisons les méthodes suivantes pour la mise en facteurs.
Si nous avons ![]() , on peut trouver deux valeurs telles que:
, on peut trouver deux valeurs telles que:
-Leur somme est de ![]()
-Leur produit est de ![]() .
.
Alors nous pourrons écrire notre expression en remplaçant ![]() par ces deux nombres.
par ces deux nombres.
Exemple:
Mettre en facteurs:
![]()
Nous avons:
![]()
![]()
![]()
Trouver 2 nombres dont la somme est ![]() et le produit est
et le produit est ![]() .
.
Avec un peu d’expérience nous voyons que ![]() et
et ![]() constituent ces deux nombres.
constituent ces deux nombres.
Nous mettons:
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} 5x^2-21x-20&=5x^2-25x+4x-20\\&=(5x^2-25x)+(4x-20)\\ &=\left[5x(x-5)+4(x-5)\right]\\&=(x-5)(5x+4) \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-be6051a12f0aa2123598c31323e425a7_l3.png)
En fin: ![]()
3- Utilisation de la formule
Pour résoudre ![]() , nous ne passons pas par les facteurs cette fois. Nous utiliserons la formule que nous venons de découvrir.
, nous ne passons pas par les facteurs cette fois. Nous utiliserons la formule que nous venons de découvrir.
Utilisons le Discriminant ![]() Avec:
Avec: ![]()
Nous avons les cas suivants:
-Lorsque ![]() nous avons deux racines comme solution.
nous avons deux racines comme solution.
![]()
-Lorsque ![]() nous avons une racine double comme solution
nous avons une racine double comme solution
![]()
-Lorsque ![]() Il n’y a pas de racines dans l’ensemble des réels
Il n’y a pas de racines dans l’ensemble des réels ![]()
(Pas de racine carrée pour les nombres négatifs dans ce cas).
4. Completer le carré:
Nous l’avons pratiquement vu ci-dessus. Nous devons isoler ![]() en ramenant tous les autres éléments au second membre.
en ramenant tous les autres éléments au second membre.
![]()
![]()
Nous savons que:
![]()
Nous obtenons: ![]()
Et puis
![]()
![]()
![]()
![]()
Finalement, la solution avec deux racines :
![]()
Exemple: Résoudre en completant:
![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de: ![]() “]
“]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Solution: ![]()
[/item] [/accordion]
Relation entre les racines d’une équation quadratique
Lorsque l’équation a deux racines, ![]() et
et ![]() dans
dans ![]() , on peut noter:
, on peut noter:
Somme des racines
(4) 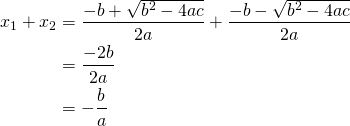
En fin:
![]()
Le produit des racines
(5) 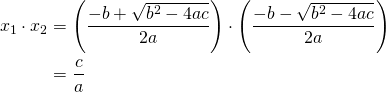
En fin:
![]()
Résoudre pour ![]()
![]()
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Cliquer ici pour voir la solution de : ![]() “]
“]
Il faut noter quet ![]()
Soit ![]()
Nous avons:
![]()
Ici:
![]()
![]()
![]()
(6) ![]()
![]()
Comme ![]() On remplace:
On remplace:
![]()
![]()
![]()
![]()
Comme ![]() On remplace:
On remplace:
![]()
![]()
![]()
![]()
Résoudre pour ![]() :
:
![]()
Nous regroupons:
![]()
![]()
![]()
![]()
Deux cas:
![]()
La seule solution:
Réponse: ![]()
Résoudre pour ![]()
![]()
Soit ![]()
Nous avons:
![]()
![]()
![]()
![]()
(7) 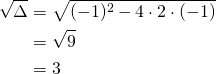
![]()
Mais ![]()
![]()
![]()
Mais ![]()
![]()
Réponse: ![]()
Résoudre en ![]()
![]()
Mais nous pouvons mettre en facteurs: ![]()
Nous obtenons: ![]() with
with ![]()
En utilisant le dénominateur commun: ![]()
![]()
![]()
![]()
Les racines:
![]()
A rejeter
![]()
Réponse: ![]()
Résoudre en ![]()
![]()
Elevant les deux membres au carré:
![]()
![]()
Elevant au carré une autre fois ![]()
![]()
![]()
La vérification montre ![]() sur chaque membre.
sur chaque membre.
Réponse: ![]()
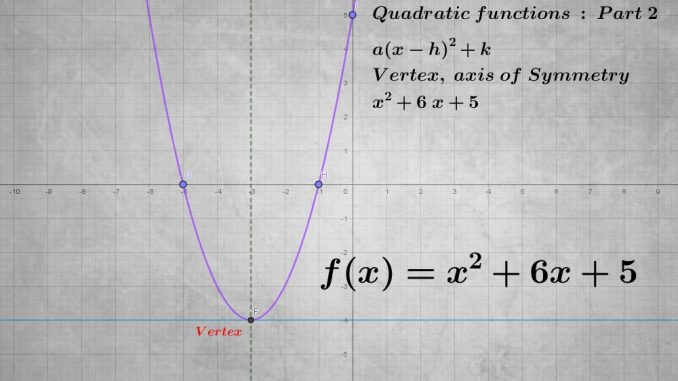
Fonctions Quadratiques
Une fonction quadratique est de la forme
![]()
Comme on le sait, a,b et c sont des nombres réels avec ![]()
Le Domaine de définition est l’ensemble des réels. ![]() est définie pour toute valeur de
est définie pour toute valeur de ![]() dans
dans ![]() .
.
![]()
Ou simplement:
![]() .
.
Nous avons appris à trouver les racines de l’équation quadratique. Nous utiliserons le même raisonnement pour tracer les courbes des quadratiques.
Intersection avec l’axe des ![]() :
:
S’obtient en posant ![]() . C’est simplement l’axe des
. C’est simplement l’axe des ![]() . La valeur de
. La valeur de ![]() est de
est de ![]() partout sur cet axe.
partout sur cet axe.
Nous avons trois cas:
Lorsque ![]() est
est ![]() , on avait deux racines.La courbe coupe l’axe des
, on avait deux racines.La courbe coupe l’axe des ![]() en deux points.
en deux points.

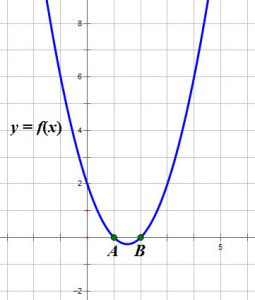
Lorsque ![]() est
est ![]() , la courbe touche l’axe des
, la courbe touche l’axe des ![]() en ce point.
en ce point.
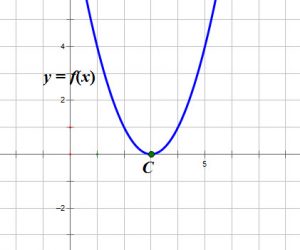
Lorsque ![]() est
est ![]() ,la courbe ne coupe /touche pas l’axe des
,la courbe ne coupe /touche pas l’axe des ![]() .
.
L’intersection de la courbe avec l’axe de ![]() est le point où cette courbe coupe l’axe des
est le point où cette courbe coupe l’axe des ![]() .
.
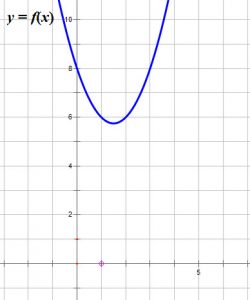
Nous pouvons l’obtenir en prenant ![]() .
.
Nous devons arranger la forme de la fonction
(8) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} (ax^2+bx+c)&=\left[a \left(x+\frac{b}{2a}\right)^2-\left(\frac{b}{2a}\right)^2+\frac{c}{a}\right]\\ &=a\left(x+\frac{b}{2a}\right)^2+\frac{4ac-b^2}{4a} \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-109723f9d837bf7ff13341a1a17019de_l3.png)
Soit
![]()
et
![]()
La fonction devient:
![]()
En traçant la courbe on voit que le point ![]() est un extremum de la fonction.
est un extremum de la fonction.
Ce point définit l’axe de symétrie.
![]() est une droite verticale qui est l’axe de symétrie de la fonction.
est une droite verticale qui est l’axe de symétrie de la fonction.
Exemple:
Tracer la courbe de ![]()
![]()
![]()
Et ![]()
![]()
On a:
![]()
Le sommet ![]()
l’intersection avec l’axe des ![]() : Lorsque
: Lorsque ![]() ,
, ![]()
Intersection avec l’axe des ![]() :
:
Les solutions:
![]()
Elle touche l’axe des ![]() au sommet.
au sommet.

Courbes diverses
Si nous utilisons la forme ![]() , nous devons pouvoir tracer les variations sans beaucoup d’efforts.
, nous devons pouvoir tracer les variations sans beaucoup d’efforts.
Partons de la base:
![]()

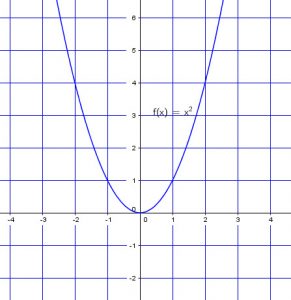
Maintenant pour ![]() , On doit mouvoir la courbe de base 1 unité à droite.
, On doit mouvoir la courbe de base 1 unité à droite.

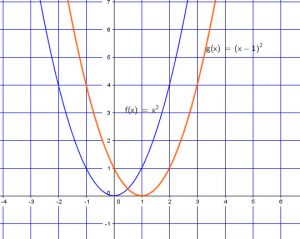
Ajoutons maintenant l’ordonnée ![]()
![]() , on deplace la courbe 2 unités en haut.
, on deplace la courbe 2 unités en haut.
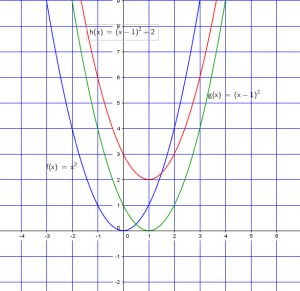
En changeant le signe de ![]()
![]() . La fonction se reflecte autour de l’axe des
. La fonction se reflecte autour de l’axe des ![]() . C’est le mirroir de la courbe de base.
. C’est le mirroir de la courbe de base.

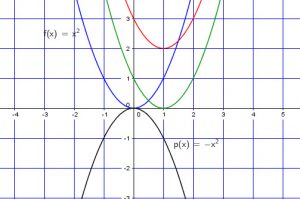
Maintenant prenons ![]() depuis la courbe de départ de:
depuis la courbe de départ de:
![]()

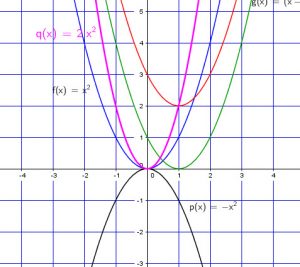
Nous pouvons ainsi dire:
-Si ![]() On renverse la courbe avant de la mouvoir.
On renverse la courbe avant de la mouvoir.
-Si ![]() , on déplace la courbe de
, on déplace la courbe de ![]() unités sur la droite.
unités sur la droite.
-Si ![]() , on déplace la courbe de
, on déplace la courbe de ![]() unités sur la gauche.
unités sur la gauche.
-Si ![]() , on déplace la courbe de
, on déplace la courbe de ![]() unités vers la haut.
unités vers la haut.
-Si ![]() , on déplace la courbe de
, on déplace la courbe de ![]() unités vers le bas.
unités vers le bas.
-Si ![]() la courbe est plus étroite.
la courbe est plus étroite.
-Si ![]() la courbe est plus élargie.
la courbe est plus élargie.
Exemple:
![]()
De ![]() ,
,
Renverser, déplacer 3 unités vers la gauche, déplacer de 2 unités en bas. Courbe est plus élargie.

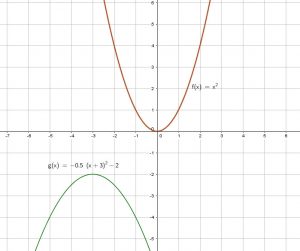
Tracer la courbe de la fonction:
![]()
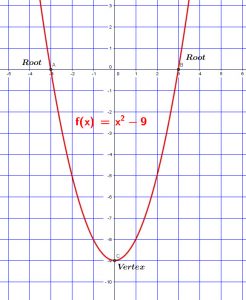
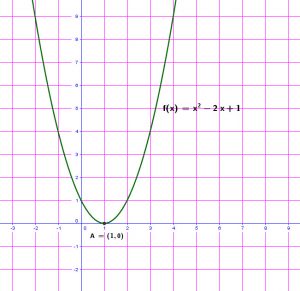
Problème 1
Une certaine Equation a sa courbe comme suit. Mettre l’Equation sous la forme ![]()

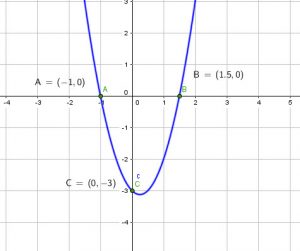
Solution:
Problème 2:
Soit:
1. Pour quelles valeurs de ![]() l’équation a deux racines?
l’équation a deux racines?
2. Trouver les valeurs de ![]() pour que l’équation ait une double racine. Calculer la racine pour chaque cas.
pour que l’équation ait une double racine. Calculer la racine pour chaque cas.
3. Trouver toutes les valeurs de ![]() rendant l’équation sans solution dans
rendant l’équation sans solution dans ![]() .
.
4. Trouver les valeurs de ![]() donnant la valeur
donnant la valeur ![]() comme l’une des racines.
comme l’une des racines.
5.En fin, trouver les valeurs de ![]() donnant le produit des racines comme
donnant le produit des racines comme ![]() .
.
Problème 3:
Soit:
1. Pour quelle valeur positive de ![]() l’équation a une double racine?
l’équation a une double racine?
2. Calculer la racine.
Solution:
![]()
Pour une double racine, le discriminant ![]() doit être
doit être ![]()
![]()
![]()
![]()
![]()
Seule valeur acceptable.
Pour ![]() nous aurons:
nous aurons:
![]()
![]()
![]()


Be the first to comment