Latest Topics

Exercise 3_20

March 25, 2020 Mouctar Algebra 0

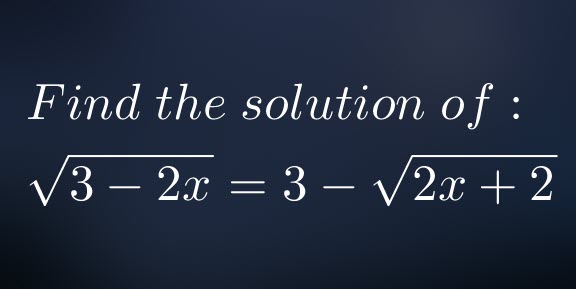
algebra20_1

Find the solution of:
$\sqrt{3-2x}=3-\sqrt{2x+2}$

Solution:
$\sqrt{3-2x}=3-\sqrt{2x+2}$

Let’s square the two sides:
We get:

$(\sqrt{3-2x})^{2}=(3-\sqrt{2x+2})^{2}$
$(3-2x)=9-6\sqrt{2x+2}+(2x+2)$
$3-2x=9-6\sqrt{2x+2}+2x+2$
Adding similar terms we get:
$3-9-2-2x-2x=-6\sqrt{2x+2}$
$-8-4x=-6\sqrt{2x+2}$

Multiplying both sides by $-\frac{1}{2}$
$2x+4=3\sqrt{2x+2}$

Let’s square both sides another time:

$(2x+4)^{2}=(3\sqrt{2x+2})^{2}$

$4x^{2}+16x+16=9(2x+2)$

$4x^{2}+16x+16=18x+18$

Divide by 2:
$2x^{2}+8x+8=9x+9$
$2x^{2}+8x+8-9x-9=0$
$2x^{2}+8x-9x+8-9=0$
$2x^{2}-x-1=0$

Let’s factor:
$2x^{2}-2x+x-1=0$
$(2x(x-1)+1(x-1)=0$
$(2x+1)(x-1)=0$
The equality is true if any factor is zero.
$2x+1=0 \Rightarrow x=-\frac{1}{2}$

The same way:
$x-1=0 \Rightarrow x=1$

If we plugin we verify that both roots are valid:

Finally:
The solution set is:

$\mathbf{\{-\frac{1}{2},{1}\}}$

Post Views: 71

Leave a Reply Cancel reply

Mouctar.org 2023, All Rights Reserved