Graphing exponential functions
The function 
is a one-to-one function (any single input gives a distinct output).
The domain of this function is 
or 
The y-intercept is 
. The x-intercept will not happen due to the nature of this function.
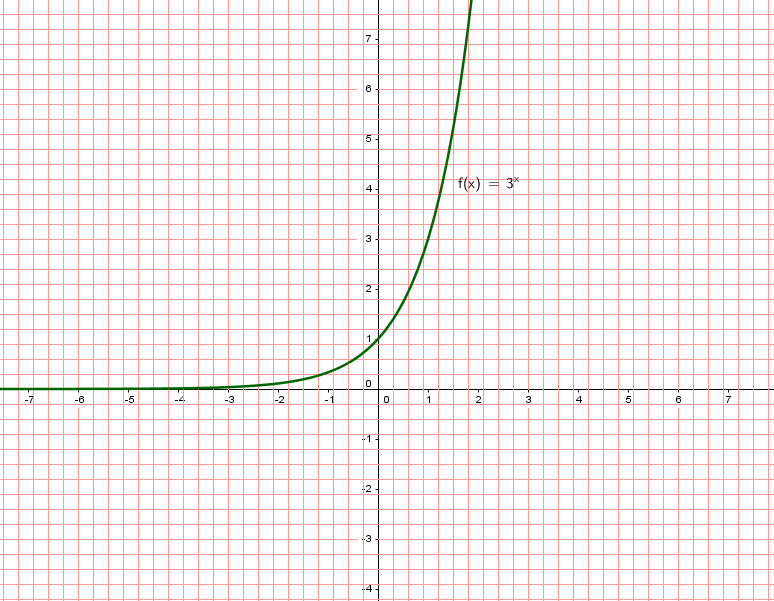
we can see that when we move towards 
the function is closer to 
but when we move to the right it increase very fast.
Rules of shifting are the same as the ones we saw with the quadratic equations.
If we flip the above equation about the 
we get 
. If we move the resulting graph 4 units down we get 
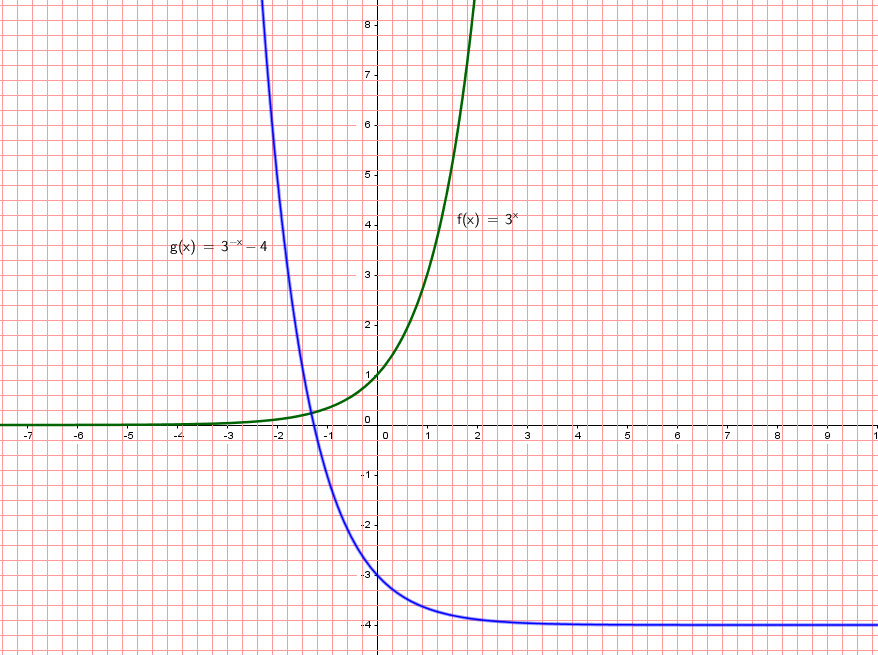
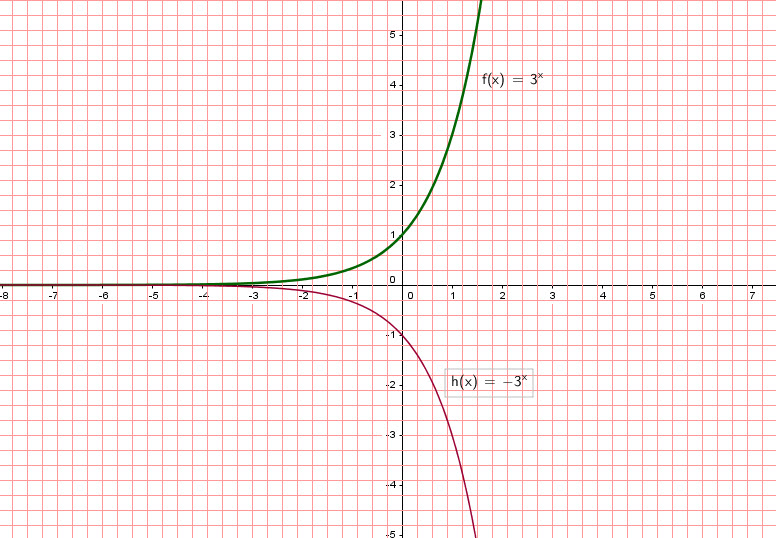
If we graph 
we get a flipped graph about the 
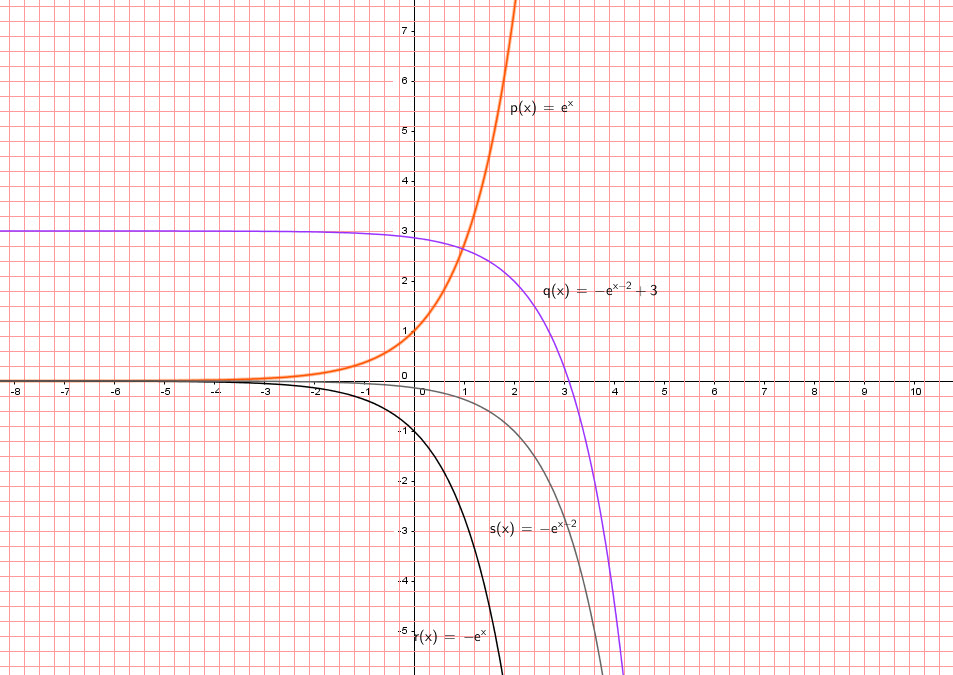
Now let’s use 
as base:
We graph 
and use transformations and draw 
Flip about , shift two units to the right and shift three units up.
Be the first to comment