Exponents and logarithms, multiple pages

Solve for $x$

$x=\log_{125}5$

We take the exponent 125 of both sides:
$125^{x}=125^{\log_{125}5}$

This is simply:
$125^{x}=5$
$5^{3x}=5^{1}$
$3x=1$
$x=\frac{1}{3}$

Answer: $x=\frac{1}{3}$

Solve for $x$

$6=\log_{3}x$

We have:
$3^6=x$
$x=729$

Answer: $x=729$

Solve for $x$

$10^x=\frac{1}{500}$

$10^x=\frac{2}{1000}$
$10^x=\frac{2}{10^3}$
$10^x=2\times 10^{-3}$
$x=\log_{10}(2\times 10^{-3})$
$x=\log_{10}(2)-3$
$x \approx -2.69897$

Solve for $x$

$2x=\log_{5}25$

We can write:
$x=\frac{1}{2}\log_{5}25$
$x=\log_{5}25^{\frac{1}{2}}$
$x=\log_{5}5$
$x=1$

Answer: $x=1$

Evaluate:
$\log_{8}8^{5}+3^{\log_{3}8}$

We can write:
$\log_{8}8^{5}+3^{\log_{3}8}=5+8$
$\log_{8}8^{5}+3^{\log_{3}8}=13$

Answer: $\log_{8}8^{5}+3^{\log_{3}8}=13$

Solve for $x$
$1+5^{x}=360$

$5^{x}=359$
$x=log_{5}359$
$x=\frac{\ln 359}{\ln 5}$
$x\approx 3.6555$

Answer: $x=\frac{\ln 359}{\ln 5}$

Solve for $x$

$2^{x+1}=30$

We write:
$2^{x+1}=30$
$x+1=\log_{2}30$
$x=\frac{\ln 30}{\ln 2}-1$

$x=\frac{\ln(15\times 2)}{\ln 2}-1$
$x=\frac{\ln 15+ \ln 2}{\ln 2}-1$
$x=\frac{\ln 15}{\ln 2}+1-1$

Answer: $x=\frac{\ln 15}{\ln 2}$

Solve for $x$ and round to the nearest hundred

$7^{-x}=0.022$

We have:

$7^{-x}=0.022$
$x=-\log_{7}0.022$
$x=-\frac{\ln 0.022}{\ln 7}$
$x\approx 1.96$

Answer: $x\approx 1.96$

Solve for $x$

$\log_{2^{x}}256=2$

We can write:
$\frac{\ln 256}{\ln (2^{x})}=2$
$\frac{\ln (2^{8})}{\ln (2^{x})}=2$
This simplifies to:
$\frac{8}{x}=2$
$2x=8$
$x=4$

Answer: $x=4$

Solve for $x$

$e^{2\ln x}=9$

We can write:

$e^{2\ln x}=9$

$e^{\ln x^{2}}=9$
$x^2=9$
$x=3$

Answer: $x=3$

Solve for $x$

$\log_{2}(x+3)=\log_{2}(x-3)+\log_{3}9+4^{\log_{4}3}$

We can write:
$\log_{2}(x+3)=\log_{2}(x-3)+\log_{3}9+4^{\log_{4}3}$

$\log_{2}(x+3)=\log_{2}(x-3)+\log_{3}3^{2}+3$
$\log_{2}(x+3)=\log_{2}(x-3)+2+3$
$\log_{2}(x+3)=\log_{2}(x-3)+5$
$\log_{2}(x+3)-\log_{2}(x-3)=5$
$\log_{2}\frac{x+3}{x-3}=5$
$\frac{x+3}{x-3}=2^{5}$
$\frac{x+3}{x-3}=32$
$x+3=32(x-3)$
$x+3=32x-96$
$31x=99$
$x=\frac{99}{31}$

Answer: $x=\frac{99}{31}$

Solve for $x$

$5^{x}=0.0016$

We have to check on $0.0016$
The reciprocal is $625$
$625=5^4$

Back to the equation:
$5^{x}=5^{-4}$
That means:
$x=-4$

Finally:

Answer: $x=-4$

Solve for $x$

$9e^{-2x}=1$

$e^{-2x}=\frac{1}{9}$
$e^{-2x}=\frac{1}{3^{2}}$
$e^{-2x}=3^{-2}$
$-2x=\ln(3^{-2}$
$-2x=-2\ln3$

Finally
$x=\ln3$

Answer: $x=\ln3$

Solve for $x$

$(e^{x}+1)(e^{\frac{x}{2}}-7)=0$

Let’s say: $e^{\frac{x}{2}}=t$

The equation becomes:
$(t^{2}+1)(t-7)=0$

Only one root here: $t^{2}+1$ is always $>0$
$t-7=0$
$t=7$
Back to $x$ notation:

$e^{\frac{x}{2}}=t$
$e^{\frac{x}{2}}=7$
$\frac{x}{2}=\ln7$
$x=2\ln7$

Finally:

Answer: $x=2\ln7$

Solve for $x$ :

$2+2\log_{3}x=\log_{3}(26x+3)$

$\log_{3}(26x+3)-\log_{3}x^{2}=2$

$\log_{3}\frac{26x+3}{x^{2}}=\log_{3}3^{2}$

We get:

$\frac{26x+3}{x^{2}}=9$

$26x+3=9x^{2}$

Re-arranging:

$9x^{2}-26x-3=0$

Solving we get:

$x_1=-\frac{1}{9}$ and $x_2=3$

But $x$ must be $>0$

The solution is : $x=3$

Solve for $x$

$\ln(x-2)+\ln(x+1)=\ln(3x-5)$

We know that:
$\ln(x-2)+\ln(x+1)=\ln{(x-2)(x+1)}$
But:
$(x-2)(x+1)=x^2-x-2$
Back to the equation:
$\ln(x-2)+\ln(x+1)=\ln(3x-5)$
$\ln{(x-2)(x+1)}=\ln(3x-5)$
If we take the exponent on both sides we get:
$(x-2)(x+1)=3x-5$
$x^2-x-2=3x-5$
$x^2-x-2-3x+5=3x-5-3x+5$
$x^2-4x+3=0$
For factoring, let’s find two numbers having a sum of $-4$ and a product of $3$ .
These two numbers are $-1$ and $-3$
We plug them in:
$x^2-4x+3=0$
$x^2-3x-x+3=0$
$x(x-3)-1(x-3)=0$
$(x-1)(x-3)=0$
The two roots are:
$x=1$
This will not work because we will have to take the $\ln(1-2)$ -Not possible.
Then $x=3$
This solution verifies our equation.
Finally:

Answer: $x=3$ .

Solve for $x$

$\ln|x+1|+\ln|x-5|=\ln16$

$\ln|(x+1)(x-5)|=\ln16$
We get:
$(x+1)(x-5)=16$ , unique case since the second will have no solution.
$x^2-4x-5=16$
$x^2-4x-21=0$
Find two numbers having a sum of $-4$ and a product of $-21$ . They are $-7$ and $3$ .
The equation becomes:
$x^2-7x+3x-21=0$
$x(x-7)+3(x-7)=0$
$(x+3)(x-7)=0$

The roots:
$x=-3$
This is a valid results that verifies our equation.
$\ln|-3+1|+\ln|-3-5|=\ln2+\ln8=\ln16$

The second root:
$x=7$
This root also verifies the equation.

Finally:
The solution is $x=-3$ and $x=7$

Solve for $x$ :

$6\ln^{2}x+7\ln(x)-3=0$

Let’s change the variable: $\ln(x)=t$
we have:
$6t^2+7t-3=0$
Find two numbers having a sum of $7$ and a product of $-18$ . These can be $9$ and $-2$
The equation becomes:
$6t^2-2t+9t-3=0$
$2t(3t-1)+3(3t-1)=0$
$(2t+3)(3t-1)=0$
The roots:
$2t+3=0$
$2t=-3$
$t=-\frac{3}{2}$
For: $\ln(x)=-\frac{3}{2}$
We get:
$x=e^{-\frac{3}{2}}$
$x=\frac{1}{\sqrt{e^3}}$

Second root:
$3t-1=0$
$3t=1$
$t=\frac{1}{3}$

With $\ln(x)=\frac{1}{3}$ ,
we get:
$x=e^{\frac{1}{3}}$
We can also write:
$x=\sqrt[3]{e}$

Solve for $x$ :

$4^{x}-3(4^{-x})=8$

We can write:
$4^{x}-3(4^{-x})=8$

$4^{x}-\frac{3}{4^{x}}=8$

$4^{x}\cdot 4^{x}-3=8\cdot 4^{x}$

We change variable: $t=4^{x}$

We get:

$t^2-8t-3=0$

$\Delta=64+12$

$\Delta=76$

$\sqrt{\Delta}=2\sqrt{19}$

$t_1=\frac{8+2\sqrt{19}}{2}$

Back to $x$

$4^{x}=\frac{8+2\sqrt{19}}{2}$

$x=\log_{4}(\frac{8+2\sqrt{19}}{2})$

$x=\log_{4}(4+\sqrt{19})$

The other value of $t$ is negative and to be rejected.

Answer: $x=\log_{4}(4+\sqrt{19})$

Solve for $x$ and $y$

$\begin{cases}{}x+y=65 \; (1)\\\ln(xy)=6\ln2 \; (2)\end{cases}$

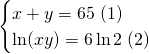
From (2) we have:

$\ln(xy)=6\ln2$
$\ln(xy)=\ln(2^{6})$
We get:
$xy=64$

From (1) we have:
$x+y=65$
$y=65-x$

In the new (2):
$xy=64$
We plug in:
$x(65-x)=64$
$65x-x^2=64$
$x^2-65x+64=0$
Find two numbers with sum $-65$ and product $64$ . They are $-64$ and $-1$ .

$x^2-65x+64=0$
$x^2-x-64x+64=0$
$x(x-1)-64(x-1)=0$
$(x-64)(x-1)=0$
The roots are:
$x=64$
and $y=65-64=1$

Finally:
The solution is:
$x=64$ and $y=1$
Or:
$x=1$ and $y=64$

Solve for $x$ and $y$

$\begin{cases}{}\ln(x^{3}y^{4})=6 \; (1)\\\ln(\frac{x^2}{y^5})=5; (2)\end{cases}$

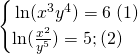
Let’s re-write:
For (1):
$\ln(x^{3}y^{4})=6$
$\ln(x^3)+\ln(y^4)=6$
$3\ln(x)+4\ln(y)=6$

For (2):
$\ln(\frac{x^2}{y^5})=5$
$\ln(x^2)-\ln(y^5)=5$
$2\ln(x)-5\ln(y)=5$

Our system can now be written:
$\begin{cases}{}3\ln(x)+4\ln(y)=6\; (11)\\2\ln(x)-5\ln(y)=5; (22)\end{cases}$

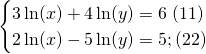
By elimination, We multiply (11) by $2$ and (12) by $-3$ and add the results up.
$6\ln(x)+8\ln(y)=12$
$-6\ln(x)+15\ln(y)=-15$
When we add:
$23\ln(y)=-3$
$ln(y)=-\frac{3}{23}$

$y=e^{-\frac{3}{23}}$
$y=\frac{1}{\sqrt[23]{e^3}}$

Now we proceed the same way to eliminate $\ln(y)$

By elimination, We multiply (11) by $5$ and (12) by $4$ and add the results up.
$15\ln(x)+20\ln(y)=30$
$8\ln(x)-20\ln(y)=20$
When we add:
$23\ln(x)=50$
$ln(x)=-\frac{50}{23}$