Exponents and logarithms, multiple pages

Solve for $x$

$5^{x}=3\times 7^{x}$

We can write:
$x\ln5=\ln 3+ x\ln7$
$x(\ln5-\ln7)=\ln3$
$x=\frac{\ln3}{\ln5-\ln7}$

We can also write:

$x=\frac{\ln3}{\ln \frac{5}{7}}$

Answer: $x=\frac{\ln3}{\ln \frac{5}{7}}$

Solve for $x$

$9^{2x+12}=\left(\frac{1}{81}\right)^{3x+2}$

We can write:
$3^{2(2x+12)}=3^{-4(3x+2)}$
$4x+24=-12x-8$
$16x=-32$
$x=-2$

Answer: $x=-2$

Solve for $x$

$3^{5x-19}=729$

We can write:
$3^{5x-19}=3^{6}$
$5x-19=6$
$5x=25$
$x=5$

Answer $x=5$

Solve for $x$

$\ln x-\frac{1}{\ln x}=\frac{15}{4}$

We write:

$\ln x-\frac{1}{\ln x}=\frac{15}{4}$

Let $\ln x=t$

The equation becomes:
$t-\frac{1}{t}=\frac{15}{4}$

To common denominator:
$4t^{2}-15t-4=0$

Find two numbers of sum $-15$ and product $-16$ . These are $-16$ and $1$ .
We write:
$4t^{2}-16t+t-4=0$
$4t(t-4)+1(t-4)=0$
$(t-4)(4t+1)=0$

First value:
$t-4=0$
$t=4$

$\ln x=4$
$x=e^{4}$

Second value:
$4t+1=0$
$4t=-1$
$t=-\frac{1}{4}$
$\ln x=-\frac{1}{4}$
$x=e^{-\frac{1}{4}}$

Or:
$x=\frac{1}{\sqrt[4]{e}}$

Answer: $x=e^{4}$ and $x=\frac{1}{\sqrt[4]{e}}$

Solve for $x$

$\ln^{3}x-2\ln^{2}x-\ln x+2=0$

Let $t=\ln x$

We can write:

$t^{3}-2t^{2}-t+2=0$

$t^{2}(t-2)-1(t-2)=0$

$(t^{2}-1)(t-2)=0$

$(t+1)(t-1)(t-2)=0$

Three roots for t:

First case:

$t+1=0 \Rightarrow t=-1$

$\ln x=-1$

$x=e^{-1}$

Second Case:

$t-1=0 \Rightarrow t=1$

$\ln x=1$

$x=e$

Third Case:

$t-2=0 \Rightarrow t=2$

$\ln x=2$

$x=e^{2}$

Answer: $x=e^{-1}$ , $x=e$ and $x=e^{2}$

Solve for $x$

$2\ln(2x-1)-\ln(3x-2x^{2})=\ln(\frac{4x-3}{x})$

We can write:

$2\ln(2x-1)-\ln(3x-2x^{2})=\ln(\frac{4x-3}{x})$
$\ln(\frac{(2x-1)^{2}}{3x-2x^{2}})=\ln(\frac{4x-3}{x})$
$\frac{(2x-1)^{2}}{3x-2x^{2}}=\frac{4x-3}{x}$
$\frac{4x^{2}-4x+1}{3x-2x^{2}}=\frac{4x-3}{x}$
$x(4x^{2}-4x+1)=(3x-2x^{2})(4x-3)$
$4x^{3}-4x^{2}+x=12x^{2}-9x-8x^{3}+6x^{2}$

In grouping by coefficients we get:

$12x^{3}-22x^{2}+10x=0$

$2x(6x^{2}-11x+5)=0$

To factor find 2 numbers with a sum $-11$ and a product of $30$ . These are $-6$ and $-5$ .

We write
$2x(6x^{2}-11x+5)=0$
$2x(6x^{2}-6x-5x+5)=0$
$2x(6x(x-1)-5(x-1))=0$
$2x(6x-5)(x-1)=0$

First case:
$x=0$
This is not acceptable in original equation.

Second case:
$x=1$

This value verifies the equation when we plug in.

Third case:
$6x-5=0$
$6x=5$
$x=\frac{5}{6}$

When we plug in: Both members value is $\ln 2 -\ln 5$

Answer: $x=1$ and $x=\frac{5}{6}$

Solve for $x$

$\ln(5x^{2}+6x+1)> 0$

We can write:

$\ln(5x^{2}+6x+1)> 0$

$\ln(5x^{2}+6x+1)> \ln 1$

$5x^{2}+6x> 0$

$x(5x+6)> 0$

We use the following table:

Factor	$x<\frac{-6}{5}$	$\frac{-6}{5}<x<0$	$x\geq 0$
$x$	$-$	$-$	$+$
$5x+6$	$-$	$+$	$+$
$x(5x+6)$	$+$	$-$	$+$

We can see the solution:

$x<-\frac{6}{5}$ and $x> 0$

Answer: $x<-\frac{6}{5}$ and $x> 0$

Solve for $x$

$\ln(x^2-10x+9)\geq \ln(3x-27)$

We can write:

$\ln(x^2-10x+9)\geq \ln(3x-27)$

$x^2-10x+9\geq 3x-27$

$x^2-13x+36 \geq 0$

Find two numbers with a sum of $-13$ and a product $36$ . These are $-9$ and $-4$
We can now re-write:

$x^2-9x-4x+36 \geq 0$

$x(x-9)-4(x-9) \geq 0$

$(x-4)(x-9) \geq 0$

We use the following table:

Factor	$x<4$	$4<x<9$	$x\geq 9$
$x-4$	$-$	$+$	$+$
$x-9$	$-$	$-$	$+$
$(x-4)(x-9)$	$+$	$-$	$+$

We can see the solution:

For $x \leq 4$ , the factor is $\geq 0$

However, this will not satisfy $\ln(3x-27)$ . So that range is to be rejected.

For $x \geq 9$ , the factor is $\geq 0$ . This value satisfies our equation

Answer: $x \geq 9$

Solve for $x$

$\ln x-\frac{1}{\ln x}< \frac{8}{3}$

We write:

$\ln x-\frac{1}{\ln x}< \frac{8}{3}$

Let $\ln x=t$

$t-\frac{1}{t}<\frac{8}{3}$

Common denominator: $3t$

$\frac{3t^{2}-3}{3t}<\frac{8t}{3t}$

$\frac{3t^{2}-8t-3}{3t}<0$

To factor we need two numbers having a sum of $-8$ and a product of $-9$ . These are $-9$ and $1$ .

$\frac{3t^2-9t+t-3}{3t}<0$

$\frac{3t(t-3)+1(t-3)}{3t}<0$

$\frac{(3t+1)(t-3)}{3t}<0$

We use the following table:

Factor	$t<-\frac{1}{3}$	$-\frac{1}{3}<0$	$0<t<3$	$t>3$
$3t+1$	$-$	$+$	$+$	$+$
$t-3$	$-$	$-$	$-$	$+$
3t	$-$	$-$	$+$	$+$
$\frac{(3t+1)(t-3)}{3t}$	$-$	$+$	$-$	$+$

We can see the solution:

The solution is : $t<-\frac{1}{3}$

Now back to $x$

$\ln x<-\frac{1}{3}$

$0<x<e^{-\frac{1}{3}}$

Or:

$0<x<\frac{1}{\sqrt[3]{e}}$

The second case:

$0<t<3$

$0<\ln x < 3$

$1<x<e^{3}$

Answer: $0<x<\frac{1}{\sqrt[3]{e}}$ , $1<x<e^{3}$

Solve for $x$ :

$\log_{2x+3} \left (6x^2+23x+21 \right)=4- \log_{3x+7} \left (4x^2+12x+9 \right)$

Our first step is to see where we can get a weak link in this equation. The designers always keep one door open.

Let’s check the factors:

(1) $\begin{equation*} \begin{split} (2x+3)^2 &=(2x)^2+2 \cdot (2x) \cdot 3+ 3^2\\ &=4x^2+12x+9 \end{split} \end{equation*}$

This is our first catch.
Let’s investigate further:

(2) $\begin{equation*} \begin{split} (2x+3) \cdot (3x+7)&=(2x) \cdot (3x)+(2x) \cdot (7)+(3) \cdot (3x)+(3)\cdot (7)\\ &=6x^2+14x+9x+21\\ &=6x^2+23x+21 \end{split} \end{equation*}$

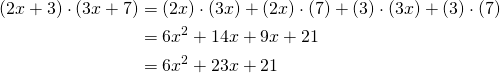
As suggested, we found two polynomials equal to the ones in the equation.
Now we need our logarithms experience:
It says:
$\log_{a} \left (x \right)=\frac{ log_{b} \left (x \right)}{ log_{b} \left (a \right)}$
Back to our factors:

$\log_{2x+3} (6x^2+23x+21)= \log_{2x+3}((2x+3)\cdot (3x+7))$

But another rule is:
$\log_{a} \left (xy \right)= \log_{a} \left (x \right)+ \log_{a} \left (y\right)$
Now we have:
$\log_{2x+3} \left (6x^2+23x+21 \right)= \log_{2x+3}(2x+3)+ \log_{2x+3}(3x+7)$
But another log rule is
$\log_{a} \left (a \right)=1$ . Even if we apply the previous rule we get 1.
That means:
$\log_{2x+3} \left (6x^2+23x+21 \right)= 1+ \log_{2x+3}(3x+7)$

On the other side of the equation:

(3) $\begin{equation*} \begin{split} \log_{3x+7} \left (4x^2+12x+9 \right)&= \log_{3x+7} (2x+3)^2\\ &=2 \log_{3x+7} \left (2x+3 \right) \end{split} \end{equation*}$

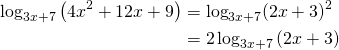
Our final equation:

$1+ \log_{2x+3}(3x+7)=4-2 \log_{3x+7} \left (2x+3 \right)$ (1*)

From what we know now we get:
$\log_{2x+3}(3x+7)=3-2 \log_{3x+7}(2x+3)$
Now let’s introduce another variable: $U$
Let $U=\log_{2x+3}(3x+7)$
That means: $\log_{3x+7} \left (2x+3 \right)=\frac{1}{U}$
From (1*):
$U=3-\frac{2}{U}$
Multiplying all by $U$ we get:
$U^2-3U+2=0$
Let’s factor this:
$U^2-2U-U+2=0$
$U(U-2)-1(U-2)=0$
$(U-1)(U-2)=0$
The solution is $U=1$ or $U=2$ ;
For $U=1$ :
$\log_{2x+3}(3x+7)=1$
It means: $3x+7=2x+3$ with a solution of $x=-4$ . Not acceptable since $3x+7$ must be $positive$
Now for $U=2$ :
$\log_{2x+3} (3x+7)=2$
It yields:
$3x+7=(2x+3)^2$
$4x^2+9x+2=0$ After simplification.
$\Delta=49$
$x_1=-\frac{1}{4}$
$x_2=-2$ (2x+3) becomes negative. Not acceptable.

Now for $x=-\frac{1}{4}$ we can easily verify that the solution is good.
Finally:

$x=-\frac{1}{4}$ is our solution.

1 2 3 4 5 6 7

Post Views: 922

Be the first to comment

Leave a Reply Cancel reply