Formula for reducing the power of the integrand

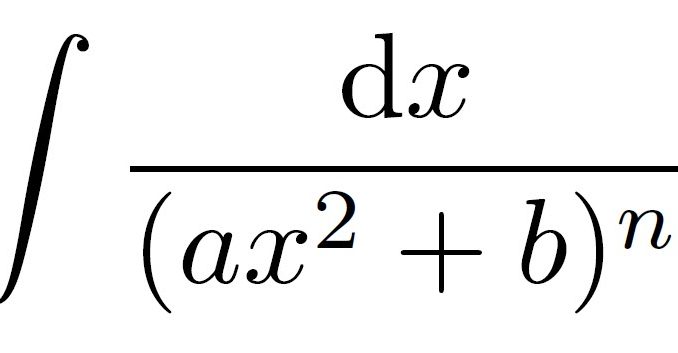
The formula is used to lower the power of the integrand to more practical powers.
If we have the following form:
$\int \frac{\mathrm{d} x}{(ax^2+b)^n}$

The general following formula should be used to solve this type of integrals.

$\int \frac{\mathrm{d} x}{(ax^2+b)^n}=\frac{x}{2b(n-a)(ax^2+b)^{n-1}}+\frac{2n-3}{2b(n-1)}\int \frac{\mathrm{d} x}{(ax^2+b)^{n-1}}$

We will work though the following example:

$\int \frac{\mathrm{d} x}{(x^2+1)^3}$

We get the following:

$a=b=1$

$n=3$

$\int \frac{\mathrm{d} x}{(x^2+1)^3}=\frac{x}{2(2)(x^2+1)^{3-1}}+\frac{3}{2(3-1)}\int \frac{\mathrm{d} x}{(x^2+1)^{3-1}}$

$\int \frac{\mathrm{d} x}{(x^2+1)^3}=\frac{x}{4(x^2+1)^{2}}+\frac{3}{4}\int \frac{\mathrm{d} x}{(x^2+1)^{2}}$

Let:

$I=\frac{3}{4}\int \frac{\mathrm{d} x}{(x^2+1)^{2}}$

${\displaystyle I=\frac{3}{4}\left[\frac{x}{2(x^2+1)}+\frac{1}{2}\int\frac{\mathrm{d} x}{(x^2+1)^{2}}}\right]$

$I=\frac{3}{8}\left[\frac{x}{(x^2+1)}+\tan^{-1}x \right]+C$

Finally:

$\int \frac{\mathrm{d} x}{(x^2+1)^3}=\frac{x}{4(x^2+1)^{2}}+\frac{3}{8}\left[\frac{x}{(x^2+1)}+\tan^{-1}x \right]+C$

Post Views: 841

Formula for reducing the power of the integrand

Be the first to comment

Leave a Reply Cancel reply