Laformule de Bretscheiner nous aide à trouver l’aire d’un quadrlatère qui n’est pas cyclique, ne pouvant autrement être inscrit dans un cercle, en utilisant seulement la longueur de ses quatres côtés et la mesure d’un angle ou de l’une des diagonales.
Nous allons trouver à partir de cette formule, une autre formule appelée la formule de Brahmagupta. Celle-là s’utilise pour les quadrilatères inscrits dans un cercle avec les angles opposés qui sont supplémentaires.
Dans ce dernier cas de figure, le produit des deux diagonales ![]() et
et ![]() est de
est de ![]() .
.
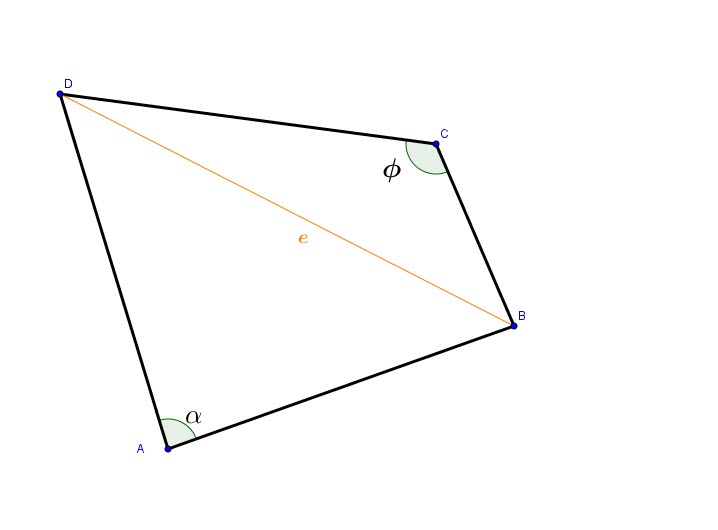
Soit ![]() l’aire de notre quadrilatère
l’aire de notre quadrilatère ![]() .
.
On remarque de la figure que ![]()
![]()
![]()
Elevant les deux membres au carré:
![]()
![]()
![]()
Prenons les deux valeurs possibles de la diagonale ![]() :
:
![]()
![]()
![]()
![]()
![]()
Elevant les deux membres au carré:
![]()
![]()
On additionne ![]() et
et ![]() :
:
![]()
![]()
![]()
![]()
![]() Le dernier terme multiplié et divisé par 2.
Le dernier terme multiplié et divisé par 2.
![]()
Au commun denominateur puis on multiplie par 4.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
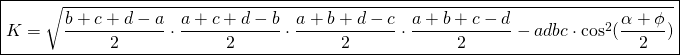
Si le demi-perimètre est de ![]()
Nous avons la formule de Bretscheiner:
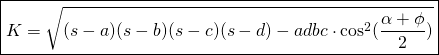
Formule de Brahmagupta
Nous utilisant un chemin similaire mais avec un quadrlatère qui est ![]() et nous savons que deux angles opposés sont supplémentaires.
et nous savons que deux angles opposés sont supplémentaires.
![]()
De la formule de Bretscheiner:
![]()
Formule de Heron
On enlève le dernier côté de la formule de Brahmagupta:
![]()
Détails approfondis:
Des lois d’Al-Kashi à Bretshneider en passant par Héron et Brahmagupta, nous allons explorer les details des formules:
Al-kashi is simply the Law of Cosines:
Loi d’Al-Kashi ou loi des cosinus:
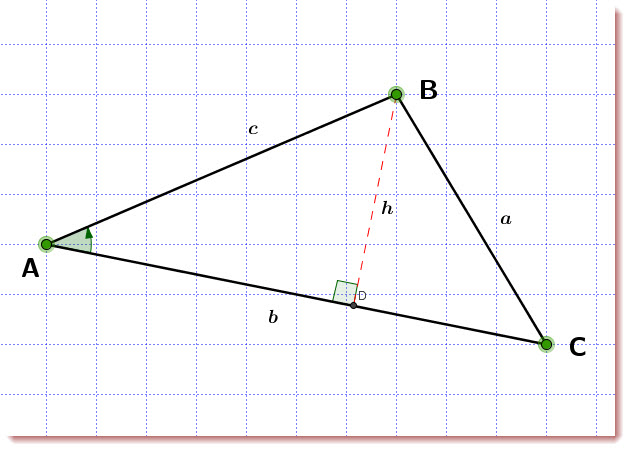
On peut voir que:
![]()
Nous avons deux triangles rectangles: ![]() and
and ![]()
Utilisant le théorème de Pythagore:
![]()
Aussi:
![]()
![]()
Mais :
![]()
Alors:
![]()
![]()
![]()
![]()
![]()
Nous savons que: ![]()
![]()
Enfin la ![]() :
:
![]()
![]()
![]()
Formula de Héron:
Calcul de l’aire du triangle avec les côtés comme données.
Soit ![]() l’aire et
l’aire et ![]() le demi-perimètre.
le demi-perimètre.
![]() .
.
Nous aurons besoin de cette formule dans les démarches qui suivent:
![]()
![]()
Mais nous savons que:
![]()
![]()
![]()
![]()
![]()
Simple difference de carrés, on factorise:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This is the Heron formula:
![]()
Formule de Bretschneider:
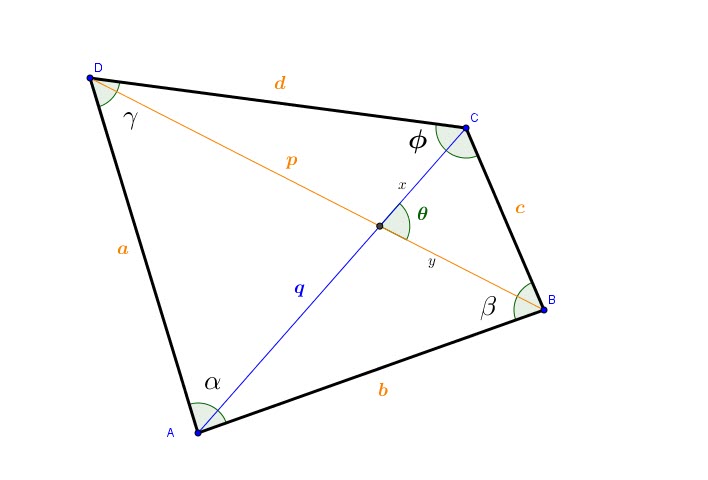
Nous allons demontrer le cacul de ces formes de l’aire ![]() selon BRETSCHNEIDER
selon BRETSCHNEIDER
![]()
![]()
![]()
On divise la diagonale ![]() en
en ![]() et
et ![]()
La même chose pour ![]() :
: ![]() and
and ![]()
On exprime l’aire des quatre triangles:
![]()
![]()
![]()
![]()
Additionnant les aires des quatre triangles:
![]()
![]()
Par simplication:
![]()
Première forme:
![]()
Maintenant la seconde forme:
De la figure:
![]()
![]()
![]()
![]()
On developpe et on remplace les termes de ![]() par
par ![]()
![]()
Continuons pour ![]()
![]()
![]()
On developpe et on remplace les termes de ![]() par
par ![]()
![]()
Continuons pour ![]()
![]()
![]()
![]()
Faisons l’addition
![]()
![]()
![]()
Par simplification:
![]()
Mais:
![]()
On remplace ![]()
![]()
Seconde Forme:
![]()
Troisième forme:
Pour les sequences précedentes:
![]()
Mais: ![]()
![]()
![]()
![]()
![]()
C’est la vraie formule de BRETSCHNEIDER:
![]()
Selon wikipedia, le travail qui suit est de COOLIDGE en 1939:
Soit ![]() l’aire de notre quadrlatère.
l’aire de notre quadrlatère.
La figure nous montre que ![]()
![]()
![]()
Elevons les deux membres au carré:
![]()
![]()
![]()
Prenons 2 valeurs de la diagonale ![]() :
:
![]()
![]()
![]()
![]()
![]()
En prenant le carré:
![]()
![]()
Adding ![]() and
and ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]() Introduction du nombre 2 dans la dernière partie de l’expression.
Introduction du nombre 2 dans la dernière partie de l’expression.
![]()
Reduction au dénominateur commun et multiplication par 4:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
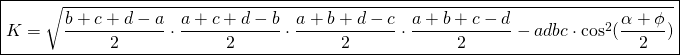
Pour un demi-perimètre ![]()
Nous avons la formule de COOLIDGE:
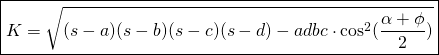
Liens externes:
http://www.planetmath.org


Be the first to comment