
Geometry lounge pack 1
Problem 1:
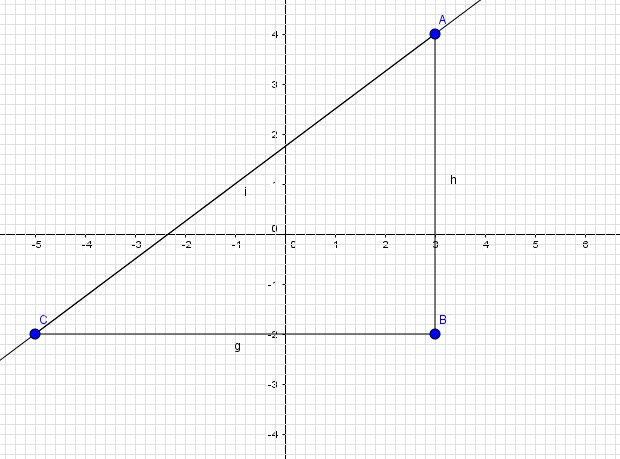
Three points A, B, C have the coordinates (3,4), (3,-2), (-5,-2) respectively
-Find which of the line segments joining the points is horizontal and what is the length?
-Which line segment is vertical and what is its length?
-What is the length of the 3rd segment and what is the equation of the line containing that segment?
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Click here to see the video solution “]
[/item] [/accordion]
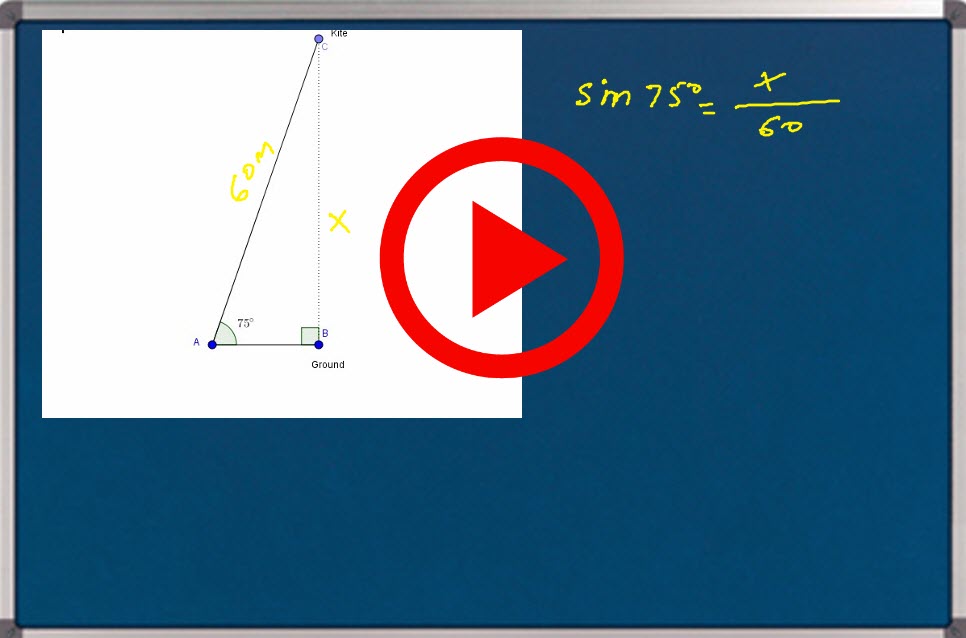
Problem 2:
A kite is flying with a length of the string already 60 meters. The string is forming a straight line making an angle of ![]() about the horizontal.
about the horizontal.
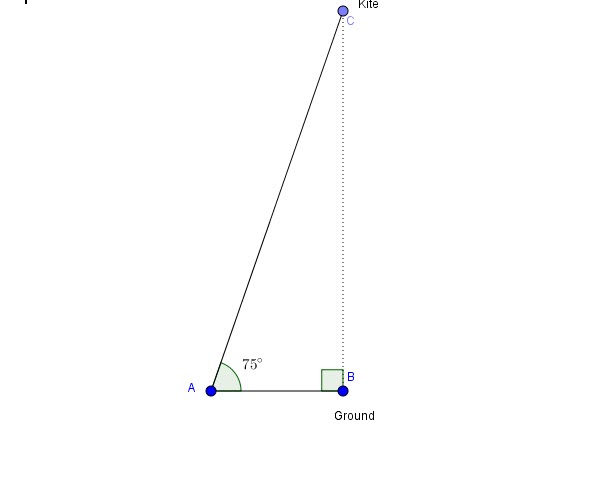
How high is it from the ground? Express your answer to the 10th of the meter.
Solution
[accordion hideSpeed=”300″ showSpeed=”400″]
[item title=”Click here to see the solution in text “]
![]()
Finally the height ![]()
![]()
[/item] [/accordion]
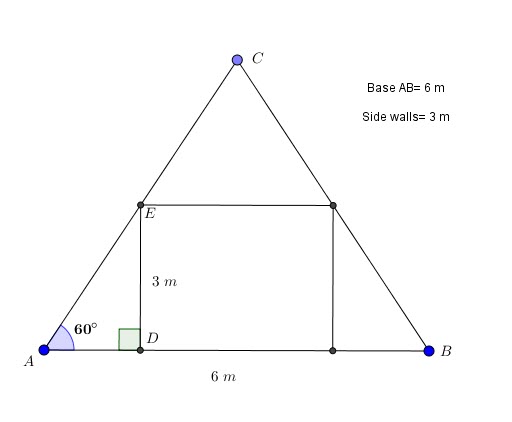
Problem 3:
An attic has a roof pitched at ![]() . A room has to be added per figure.
. A room has to be added per figure.
How far away from the sides must the walls be built?
What is the front area of the room?
Solution:
We have ![]()
![]()
![]()
Base of room:
![]()
Area of the front:
![]()
Problem 4:
A rectangular-shaped garden with sides of lengths 16 feet and 9 feet.
It has been decided that the garden has to be changed into a square design with the same design as the original rectangular-shaped garden.
What will be the measure of the side of the new square-shaped garden?
Solution:
If ![]() is the side of the square
is the side of the square
![]()
![]()
Problem 5:
The central angle of measure ![]() is subtended by a circular arc of length 6 meters.
is subtended by a circular arc of length 6 meters.
What is the radius of the circle?
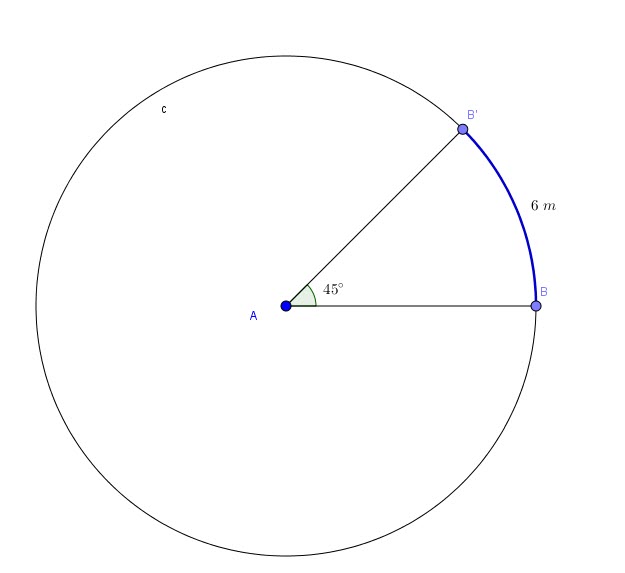
Solution:
The length of the arc:
![]()
In this problem ![]() and
and ![]()
![]()
![]()
Problem 6:
A rectangular box with a base 2 inches by 6 inches is 10 inches tall and holds 12 ounces of breakfast cereal.
The manufacturer wants to use a new box with a base of 3 inches by 5 inches.
How many inches tall should the new box be in order to hold exactly the same volume as the original box?
Solution:
This is a classic problem that will come back in other packs.
It is important to understand the concept:
The two volumes are equal.
If ![]() is the new height:
is the new height:
We simply make the volumes identical
![]()
![]()
![]()
Problem 7:
Circle c is centered at A and the small circle is tangent to circle c.
What is the value of the colored area if ![]() units?
units?
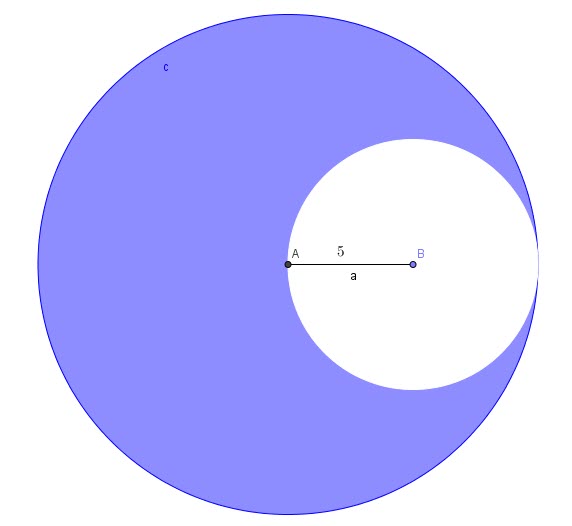
Solution:
From the graph we can depict that:
For the big circle: ![]()
For the small circle: ![]()
The colored area is simply the difference between the two areas
![]()
Problem 8:
A 6-foot spruce tree is planted 15 feet from a lighted streetlight whose lamp is 18 feet above the ground.
How many feet long is the shadow of that tree?
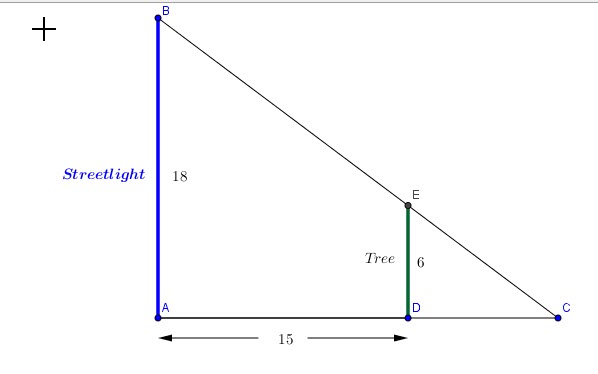
Solution:
![]() by
by ![]() postulate
postulate
If ![]()
![]()
But ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Problem 9:
Given DE=12, EF=7 and FG=10, What is the area of ![]() ?
?
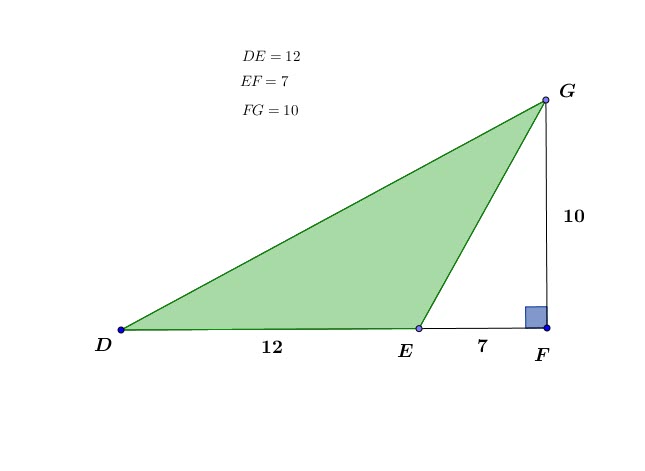
Solution:
We have to find the difference between areas of ![]() and
and ![]()
Colored area ![]()
![]() or simply
or simply ![]() has a base of
has a base of ![]() and a height of
and a height of ![]()
![]()
Problem 10:
Given the triangle ABC, what is ![]() ?
?
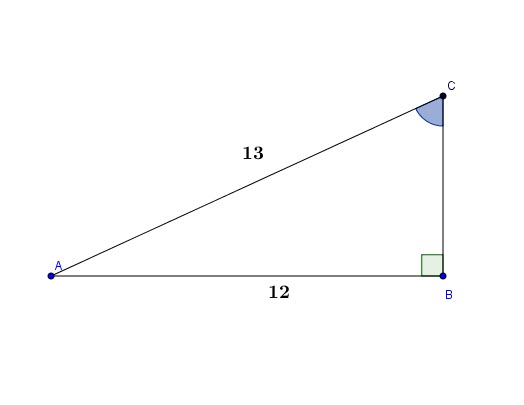
Solution:
![]()
Problem 11:
In the following figure:
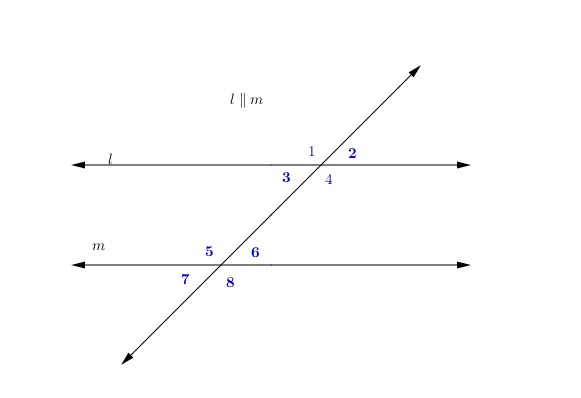
![]()
![]()
Find ![]() and find the measure of all angles
and find the measure of all angles
Solution
Looking at the graph, ![]() and
and ![]() are corresponding angles and they are supplementary to
are corresponding angles and they are supplementary to ![]()
That means:
![]()
We get:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finally:
Angles: 2,3,6,and 7 all have same measure of ![]()
Angles: 1,4,5,and 8 all have same measure of ![]()
Problem 12:
In the following figure:
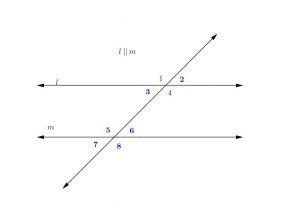
![]()
![]()
Find ![]() and find the measure of all angles
and find the measure of all angles
Solution
Looking at the graph, ![]() and
and ![]() are on the same side of transversal and are supplementary.
are on the same side of transversal and are supplementary.
That means:
![]()
We get:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finally:
Angles: 2,3,6,and 7 all have same measure of ![]()
Angles: 1,4,5,and 8 all have same measure of ![]()
Problem 13:
In the following figure:

![]()
![]()
Find ![]() and find the measure of all angles
and find the measure of all angles
Solution
![]() and
and ![]() interior are alternate interior angles.
interior are alternate interior angles.
Alternate interior angles are congruent.
![]()
![]()
That yields:
![]()
![]()
![]()
![]()
We plug in:
![]()
![]()
![]()
![]()
Problem 14:
In the following figure:

![]()
![]()
Find ![]() and find the measure of all angles
and find the measure of all angles
Solution
![]() and
and ![]() are alternate exterior angles and therefore congruent.
are alternate exterior angles and therefore congruent.
![]()
![]()
That yields:
![]()
![]()
![]()
![]()
![]()
![]()
Case 1:
![]() and
and ![]()
![]()
![]()
Case 2:
![]() and
and ![]()
![]()
![]()
Problem 15:
In the following figure:
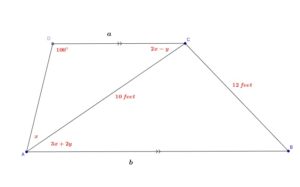
![]() and
and ![]()
1. Find the values of ![]() and
and ![]()
2. Find ![]()
3.Find ![]() and
and ![]()
4. Find the area of figure ![]()
Solution:
From ![]()
![]()
![]()
![]()
![]()
From transversal ![]() :
:
![]()
![]()
![]()
![]()
![]()
Adding ![]() and
and ![]() :
:
![]()
![]()
From ![]()
![]()
![]()
![]()
![]()
![]()
Finding ![]()
![]()
![]()
![]() . This verifies the sum of
. This verifies the sum of ![]()
![]()
From ![]() :
:
![]()
Finding the height ![]()
![]()
Finding ![]() and
and ![]() :
:
![]()
![]()
![]()
Problem 16
Solve the triangle shown for
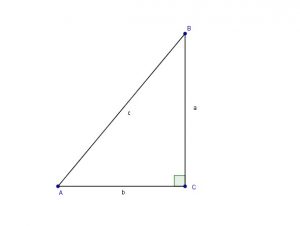
![]() and
and ![]()
Solution:
Solve for ![]()
We have to make sure that all 6 elements have been calculated.
ANGLES
![]()
![]()
![]()
SIDES:
![]()
![]()
![]()
This is the right triangle geometry:
![]()
![]()
Now let’s calculate ![]() and check it:
and check it:
![]()
Now let’s verify:
![]()
This verifies the length of ![]()
Answer:
ANGLES
![]()
![]()
![]()
SIDES:
![]()
![]()
![]()
Problem 17
Solve the triangle shown for

![]() and
and ![]()
SOLUTION
ANGLES
![]()
![]()
![]()
SIDES:
![]()
![]()
![]()
Here we have to find ![]() ,
, ![]() and length side
and length side ![]() .
.
We are lucky it is a right triangle, easy.
![]()
Now ![]()
We used the ![]() function for we knew that since the sum of the two angles was 90, none would exceed 90.
function for we knew that since the sum of the two angles was 90, none would exceed 90.
Finding the last element ![]()
![]()
Now let’s verify:
![]()
This verifies the length of ![]()
Answer:
ANGLES
![]()
![]()
![]()
SIDES:
![]()
![]()
![]()
Problem 18
An observer on the earth observes an airplane flying overhead that subtends an angle of ![]() .
.
If the plane is known to have a length of ![]() , what is its altitude to nearest hundred feet?
, what is its altitude to nearest hundred feet?
See figure.
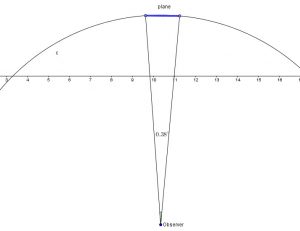
SOLUTION
Here we can use two methods but it does not matter at that distance since the arc and the straight line representing the length of the plane are the same
![]() rounded the 100 feet accuracy.
rounded the 100 feet accuracy.
Problem 19
A curve along a highway is an arc of a circle with 250-meter radius. If the curve corresponds to a central angle of 2 radians, what is the length of the highway along the curve?
SOLUTION
The curve:
![]()
Problem 20:
Given:
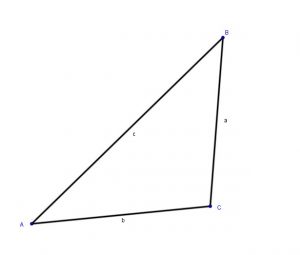
![]()
![]()
![]()
Find the other elements if the triangle is possible.
SOLUTION
ANGLES
![]()
![]() C=?
C=?
SIDES:
![]()
![]()
![]()
We notice that side ![]() this means that
this means that ![]()
We can safely use the LAW OF SINES:
![]()
![]()
![]()
For side c:
![]()
Answer:
ANGLES
![]()
![]()
![]()
SIDES:
![]()
![]()
![]()
We also verify that ![]() because
because ![]()
Problem 21:
![]()
![]()
![]()
Find the other elements if the triangle is possible.
SOLUTION
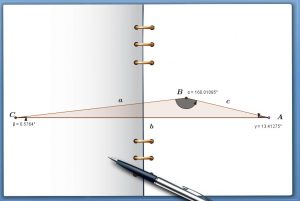
ANGLES
![]()
![]()
![]()
SIDES:
![]()
![]()
![]()
We notice the the sum of the measures of ![]() and
and ![]() is only
is only ![]()
Let’s try to calculate:
![]()
![]()
![]()
Answer:
ANGLES
![]()
![]()
![]()
SIDES:
![]()
![]()
![]()
Problem 22:
![]()
![]()
![]()
Find the other elements if the triangle is possible.
SOLUTION
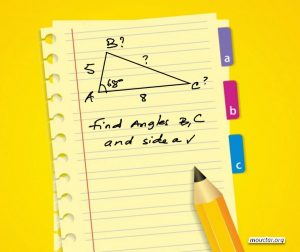
ANGLES
![]()
![]() C=?
C=?
SIDES:
![]()
![]()
![]()
We notice that side ![]() this means that
this means that ![]()
But in this case we don’t know if one angle is obtuse. We use the law of cosines.
Side ![]()
![]()
![]()
For ![]()
![]()
![]()
Answer:
ANGLES
![]()
![]()
![]()
SIDES:
![]()
![]()
![]()
Problem 23:
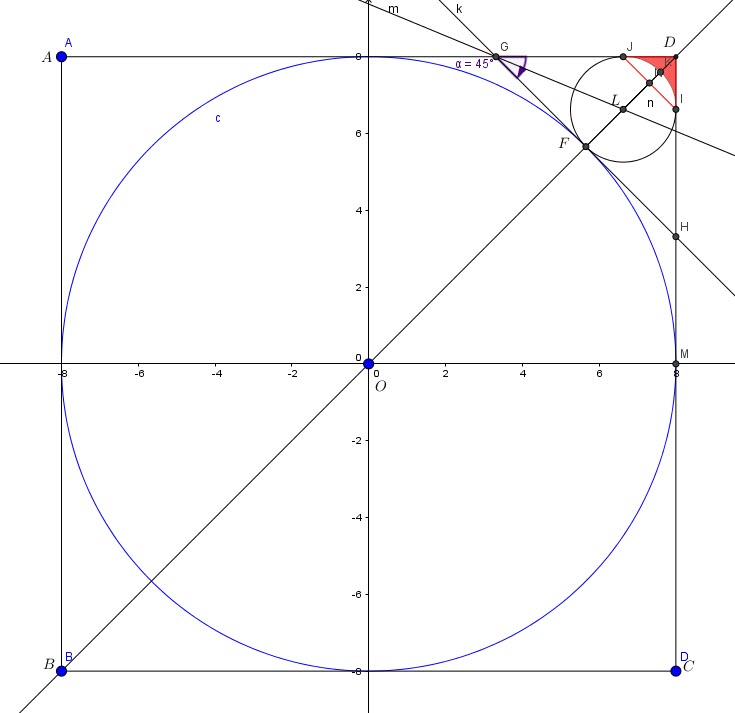
A circle of center ![]() has been inscribed in a square ABCD, of side 16 meters.
has been inscribed in a square ABCD, of side 16 meters.
In the following figure, a smaller circle of center ![]() and tangent of Circle
and tangent of Circle ![]() at
at ![]() has been inscribed per figure.
has been inscribed per figure.
1. What is the equation of ![]() ?
?
2. What is the equation of the small circle ![]() ?
?
3.What is the area of the colored area?
(All calculations to be to the thousandth)

For video solution

For text:
The circle center ![]()
General Equation of a circle of center ![]() is:
is:
![]()
We can see that the radius is half of the width of the square.
![]()
![]()
Now let’s draw aline passing through points ![]() and
and ![]()
Points ![]() coordinates
coordinates ![]()
Distance ![]() :
:
![]()
Distance ![]()
![]()
The line passing through ![]()
![]()
It’s perpendicular line ![]() has a slope of
has a slope of ![]() .
.
That line passes through the tangency point ![]() .
.
Coordinates of ![]()
![]()
For point ![]() :
:
![]()
Line ![]() passes through
passes through ![]() with a slope of
with a slope of ![]() . We use the general form:
. We use the general form:
![]()
![]()
![]()
![]()
This is the equation of line ![]() .
.
![]()
Line ![]() meets the square in two points
meets the square in two points ![]() and
and ![]()
For point ![]() :
:
Point ![]() is the intersection of lines
is the intersection of lines ![]() and line
and line ![]() or
or ![]()
We get at ![]() :
:
![]()
![]()
![]()
Finally:
![]()
Or:
![]()
For point ![]() :
:
Point ![]() is the intersection of lines
is the intersection of lines ![]() and line
and line ![]() or
or ![]()
Let’s plug in the value of ![]() :
:
For point ![]() :
:
![]()
So:
![]()
Or:
![]()
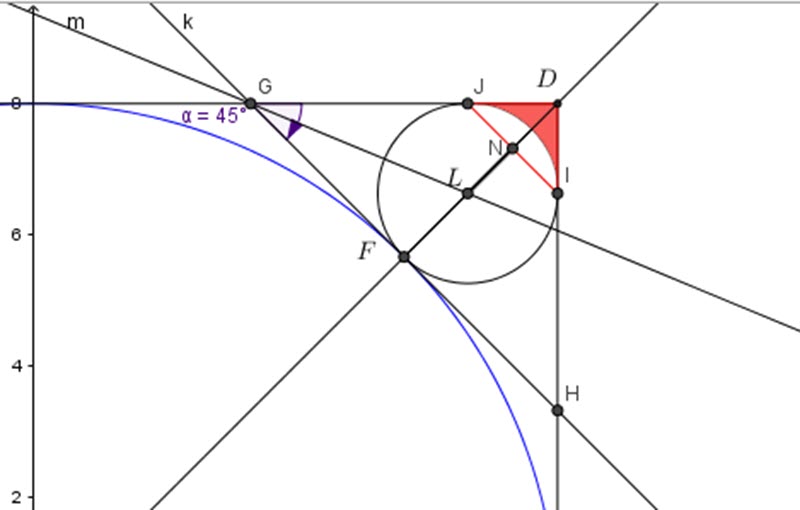
Now we can see the triangle ![]()
Circle ![]() is inscribed in
is inscribed in ![]() with
with ![]() being the incerter.
being the incerter.
Lines from any vertex bisects that vertex.
We see that angle:
![]()
The line from vertex ![]() to
to ![]() will make an angle of
will make an angle of ![]()
Let’s find it’s tangent or the slope.
![]()
From our formula page:
![]()
![]()
![]()
![]() . This is the slope.
. This is the slope.
The line ![]() passes through
passes through ![]()
![]()
We use the standard equation:
![]()
![]()
![]()
![]()
![]()
The lines ![]() and
and ![]() intersect at the incenter
intersect at the incenter ![]() , center of
, center of ![]()
We get:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Since the point ![]() is on
is on ![]() :
:
![]()
The length ![]() is the radius of
is the radius of ![]()
Let’s calculate that distance:
![]()
![]()
![]()
![]()
![]()
![]()
If ![]() is the radius of
is the radius of ![]() :
:
![]()
Let’s use decimals to simplify:
![]()
Equation of the circle:
![]()
Or in decimals:
![]()
Now for the final question we have to take a look at the graph:
The shaded is simply the difference between the areas of ![]() and circle segment of arc
and circle segment of arc ![]()
Let’s calculate that difference.
Triangle ![]() is a right triangle.
is a right triangle.
The circle segment intercepts an arc with a central angle of ![]()
![]() with
with ![]() in our case.
in our case.
![]()
![]()
![]()
Area of ![]()
Let’s calculate the length of segment ![]()
The height of ![]() is:
is:
![]() with
with ![]()
We can see that : ![]()
![]()
![]()
In the right triangle ![]()
![]()
![]()
![]()
We can also say that ![]() without approximation for
without approximation for ![]() is the intersection of the diagonals of the quadrilateral
is the intersection of the diagonals of the quadrilateral ![]()
Finally:
![]()
![]()
Area of ![]() is:
is:
![]()
Shaded Area:
![]()
Answer: ![]()
Problem 24:
The isosceles trapezoid, ABCD, shown in the following figure has the parallel sides measuring 8 meters and 18 meters.
1. Find the area of the inscribed circle.
2. Find the value of the shaded area inside the trapezoid.
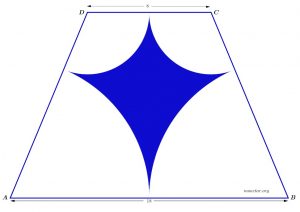
[accordion hideSpeed=”300″ showSpeed=”400″] [item title=”Click here to see the video solution “]
[/item] [/accordion]
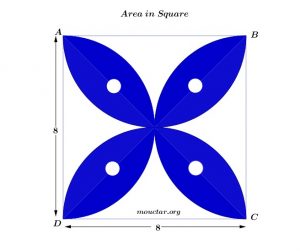
Problem 25:
Find the value of the blue shaded area in the following design. The area is inside a square with a side of 8 meters. The four holes are circles with 600 millimeters as diameter each.
Round your result to the hundredth.
Problem 26
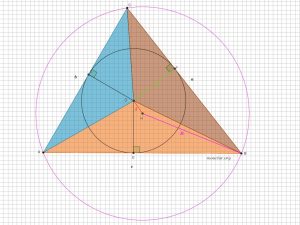
In the following figure the triangle has sides ![]() . The semiperimeter is
. The semiperimeter is ![]()
1. Show that the radius of the inscribed circle can be expressed as:
![]()
2.Show that the area can be expressed as:
![]()
3. Find the radius ![]() of the circumcircle using any of the known formulas.
of the circumcircle using any of the known formulas.
4. What is the distance ![]() between the centers of the two circles?
between the centers of the two circles?
Verify your result using ![]()
5. If ![]() , express the radius
, express the radius ![]() of the incircle as:
of the incircle as:
![]()
6. Show the values of ![]() ,
, ![]() and
and ![]() using the following:
using the following:
a. ![]() ,
, ![]() and
and ![]()
b. ![]() ,
, ![]() and
and ![]()



Be the first to comment