Latest Topics

Inscribed Circles from the Lounge

December 26, 2016 Mouctar Analytic geometry 0

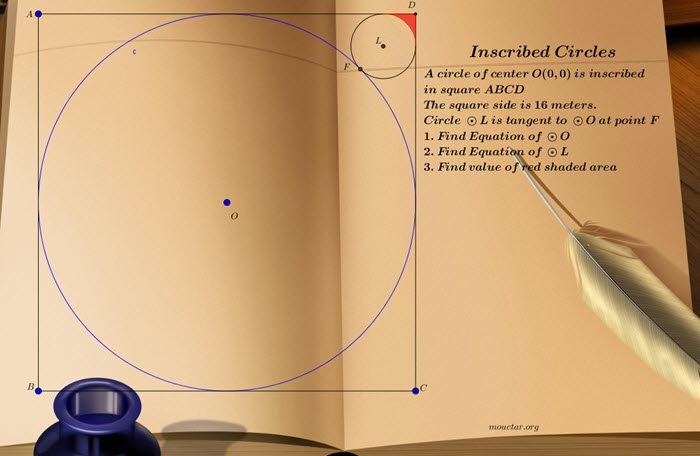
images_lounge23

Inscribed circles, from the lounge

Problem 23:

A circle of center $O(0,0)$ has been inscribed in a square ABCD, of side 16 meters.

In the following figure, a smaller circle of center $L$ and tangent of Circle $\odot O$ at $F$ has been inscribed per figure.

1. What is the equation of $\odot O$ ?
2. What is the equation of the small circle $\odot L$ ?

3.What is the area of the colored area?

(All calculations to be to the thousandth)

SOLUTION

The circle center $O(0,0)$

General Equation of a circle of center $(x_0, y_0)$ is:

$(x-x_0)^{2}+(y-y_0)^{2}=R^{2}$

We can see that the radius is half of the width of the square.

$R=8$

$(x)^{2}+(y)^{2}=8^{2}$

Now let’s draw aline passing through points $O$ and $D$

Points $D$ coordinates $D=(8,8)$

Distance $OD$ :

$OD^{2}=8^2+8^2 \Rightarrow OD=8 \sqrt{2}$

Distance $FD$

$FD=OD-OF=8 \sqrt{2}-8=8(\sqrt{2}-1)$

The line passing through $O \& D$

$y=x$

It’s perpendicular line $k$ has a slope of $m'=-1$ .

That line passes through the tangency point $F$ .

Coordinates of $F$

$\cos \frac{\pi}{4}=\frac{x_F}{R} \Rightarrow x=R \cos \frac{\pi}{4}=\frac{8 \sqrt{2}}{2}=4 \sqrt{2}$

For point $F$ :

$F=(4 \sqrt{2}, 4 \sqrt{2})$

Line $k$ passes through $F$ with a slope of $-1$ . We use the general form:

$y-y_0=m(x-x_0)$

$y-4\sqrt{2}=-1(x-4\sqrt{2})$

$y=-x+4\sqrt{2}+4\sqrt{2}$

$y=-x+8\sqrt{2}$

This is the equation of line $k$ .

$x+y=8\sqrt{2}$

Line $k$ meets the square in two points $G$ and $H$

For point $G$ :

Point $G$ is the intersection of lines $y=8$ and line $k$ or $y=-x+8\sqrt{2}$

We get at $G$ :

$-x+8\sqrt{2}=8$

$x=8\sqrt{2}-8$

$x=8(\sqrt{2}-1)$

Finally:

$G=(8(\sqrt{2}-1), 8)$

Or:

$G=(3.314, 8)$

For point $H$ :

Point $H$ is the intersection of lines $x=8$ and line $k$ or $y=-x+8\sqrt{2}$

Let’s plug in the value of $x$ :

For point $H$ :

$y=-x+8\sqrt{2}=-8+8\sqrt{2}=8(\sqrt{2}-1)$

So:

$H=(8,8(\sqrt{2}-1))$

Or:

$H=(8,3.314)$

Now we can see the triangle $\triangle GDH$

Circle $\odot L$ is inscribed in $\triangle GDH$ with $L$ being the incenter.

Lines from any vertex bisects that vertex.

We see that angle:

$m\angle FGD=\frac{\pi}{4}$

The line from vertex $G$ to $L$ will make an angle of $-\frac{\pi}{8}$

Let’s find it’s tangent or the slope.

$\tan (-\frac{\pi}{8})=-\tan \frac{\pi}{8}$

From our formula page:

$\tan \theta=\frac{1-\cos 2\theta}{\sin 2\theta}$

$\tan \frac{\pi}{8}=\frac{1-\cos \frac{\pi}{4}}{\sin \frac{\pi}{4}}$

$\tan \frac{\pi}{8}=\frac{1-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}=\sqrt{2}-1$

$\tan (-\frac{\pi}{8})=-(\sqrt{2}-1)$ . This is the slope.

The line $m$ passes through $G$

$G=(8(\sqrt{2}-1), 8)$

We use the standard equation:

$y-y_G=m(x-x_G)$

$y-8=-(\sqrt{2}-1)(x-8(\sqrt{2}-1))$

$y=-(\sqrt{2}-1)x+8(2-2\sqrt{2}+1)+8$

$y=-(\sqrt{2}-1)x+8(2-2\sqrt{2}+1+1)$

$y=-(\sqrt{2}-1)x+16(2-\sqrt{2})$

The lines $y=x$ and $y=-(\sqrt{2}-1)x+16(2-\sqrt{2})$ intersect at the incenter $L$ , center of $\odot L$

We get:

$x=-(\sqrt{2}-1)x+16(2-\sqrt{2})$

$x(1-\sqrt{2}-1)=16(2-\sqrt{2})$

$x\sqrt{2}=16(2-\sqrt{2})$

$x=\frac{16(2-\sqrt{2})}{\sqrt{2}}$

$x=\frac{16\sqrt{2}(2-\sqrt{2})}{2}$

$x=8(2\sqrt{2}-2)$

$x=16(\sqrt{2}-1)$

Since the point $L$ is on $y=x$ :

$L=(16(\sqrt{2}-1), 16(\sqrt{2}-1))$

The length $FL$ is the radius of $\odot L$

Let’s calculate that distance:

$F=(4 \sqrt{2}, 4 \sqrt{2})$

$L=(16(\sqrt{2}-1), 16(\sqrt{2}-1))$

$FL=\sqrt{(16\sqrt{2}-16-4\sqrt{2})^{2}+(16\sqrt{2}-16-4\sqrt{2})^{2}}$

$FL=\sqrt{2(16\sqrt{2}-16-4\sqrt{2})^{2}}$

$FL=\sqrt{2}(12\sqrt{2}-16)$

$FL=24-16\sqrt{2}$

If $r$ is the radius of $\odot L$ :

$r=24 -16 \sqrt{2}$

Let’s use decimals to simplify:

$r=1.373$

Equation of the circle:

$(x-16(\sqrt{2}-1))^{2}+(y-16(\sqrt{2}-1))^{2}=( 24-16\sqrt{2})^{2}$

Or in decimals:

$(x-6.627)^{2}+(y-6.627)^{2}=(1.373)^{2}$

Now for the final question we have to take a look at the graph:

The shaded is simply the difference between the areas of $\triangle JID$ and circle segment of arc $IJ$

Let’s calculate that difference.

Triangle $\triangle LJI$ is a right triangle.

The circle segment intercepts an arc with a central angle of $\frac{\pi}{2}$

$Area\;of\;segment=\frac{1}{2}r^{2}(\alpha-\sin \alpha)$ with $\alpha=\frac{\pi}{2}$ in our case.

$Area\;of\;segment=\frac{1}{2}(1.373)^{2}(\frac{\pi}{2}-\sin \frac{\pi}{2})$

$Area\;of\;segment=0.942(\frac{\pi}{2}-1)=0.942(0.571)$

$Area\;of\;segment=0.538$

Area of $\triangle JID$

Let’s calculate the length of segment $LN$

The height of $\triangle JID$ is:

$DN=OD-ON$ with $ON=OF+FL+LN=R+r+LN$

We can see that : $DN=OD-R-r-LN=8\sqrt{2}-8-24+16\sqrt{2}-LN$

$JI=r \sqrt{2}=(24-16\sqrt{2})\sqrt{2}=24 \sqrt{2}-32=1.941$

$NI=\frac{1}{2}JI=0.971$

In the right triangle $\triangle LNI$

$r^2=(NI)^{2}+(LN)^{2}$

$LN=\sqrt{r^{2}-(NI)^{2}{2}}=\sqrt{1.884-(0.971)^{2}}$

$LN=\sqrt{1.884-0.943}=\sqrt{0.941}=0.970$

We can also say that $LN=ND=0.971$ without approximation for $N$ is the intersection of the diagonals of the quadrilateral $DJLI$

Finally:

$DN=8\sqrt{2}-8-24+16\sqrt{2}-0.970=11.314-8-24+22.627-0.970=0.971$

$DN=0.971$

Area of $\triangle JID$ is:

$Area\; \triangle JID=\frac{1}{2}JI \cdot DN=\frac{1}{2}1.941 \times 0.971=0.942\; m^{2}$

Shaded Area:

$Shaded\; Area=0.942-0.538=0.404$

Answer: $Shaded\; Area=0.404\; m^{2}$

Post Views: 71

Leave a Reply Cancel reply

Mouctar.org 2023, All Rights Reserved