
Hyperbolic functions
We have used some hyperbolic functions relations in some of our chapters.
This is a summary of these functions to enable us to use them in future chapters.
We’ll go through their definitions and we’ll use the similarities with the regular trigonometric functions to see most of the formulas.
| Equation | |
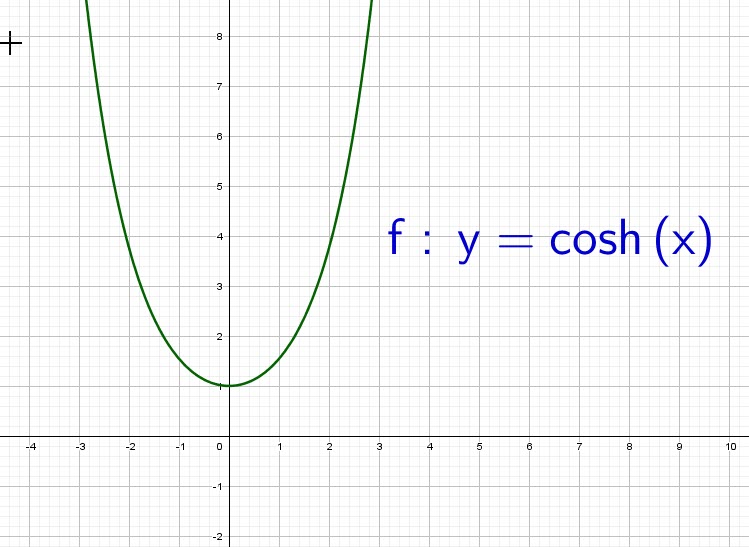
Hyperbolic cosine function
The ![]() noted
noted ![]() is defined as follows:
is defined as follows:
![]()
This straight forward definition will be used to generate other formulas.
Hyperbolic sine function
The ![]() noted
noted ![]() is defined as follows:
is defined as follows:
![]()
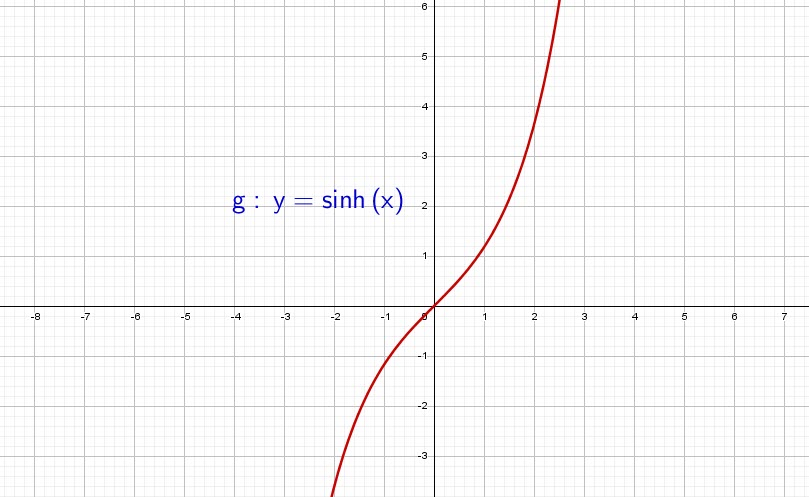
This straight forward definition will be used to generate other formulas.
Other hyperbolic functions
Without any surprise we can write:
![]()
We get
![]()
Please note:
![]()
When we note:
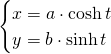
When ![]() changes in the real numbers, the points
changes in the real numbers, the points ![]() follow one branch of the hyperbola.
follow one branch of the hyperbola.
Hyperbolic Trigonometry
![]()
![]()
![]() This shows that
This shows that ![]()
We can also show that:
![]()
Sum and Difference formulas
Using the above relations we can get:
![]()
![]()
![]()
![]()
Double angle
![]()
![]()
For the tangents:
![]()
![]()
![]()
Transformation formulas
From the formulas shown above, we can get:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
If we have ![]()
From above we get:
![]()
![]()
![]()
Inverse hyperbolic functions:
Let ![]()
We can write:
![]() with
with ![]()
But we know:
![]()
We plugin:
![]()
Taking the ![]() of both sides:
of both sides:
![]()
Let ![]()
We can write:
![]() with
with ![]()
But we know:
![]()
We plugin:
![]()
Taking the ![]() of both sides:
of both sides:
![]()
Problem 1:
Prove the sum formula below:
![]()
Solution
To solve this problem we use the following formulas:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The same way we can prove that
![]()
Back to the formula
(1) 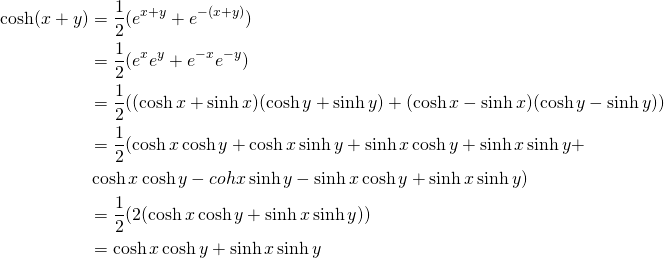


Be the first to comment