Indefinite Integral
We have covered the introduction to derivatives. Another topic would be to find a function if we know it’s derivative.
This very interesting and we won’t spend much time explaining what the antiderivative is in that case.
A function ![]() is an antiderivative of the function
is an antiderivative of the function ![]() if
if ![]() for all
for all ![]() in the domain of
in the domain of ![]() .
.
The only problem is when we calculated the derivative of a constant ![]() , we found
, we found ![]() .
.
Let’s check the following fact:
If we have ![]()
We know that ![]()
But so is: ![]() .
.
And we can add any constant, the derivative will be the same.
We get the theorem:
Theorem: General form of antiderivatives
Let ![]() be an antiderivative of
be an antiderivative of ![]() over an interval
over an interval ![]() . Then,
. Then,
1. For each constant ![]() , the function
, the function ![]() is also an antiderivative of
is also an antiderivative of ![]() over
over ![]() .
.
2. If ![]() is an antiderivative of
is an antiderivative of ![]() over
over ![]() , there is a constant
, there is a constant ![]() for which
for which ![]() over
over ![]() .
.
Meaning, the general form of the antiderivative of ![]() over
over ![]() is
is ![]() .
.
EXAMPLE:
Find the antiderative of ![]()
We can see that it is ![]()
Indefinite Integrals
This is the notation used for the antiderivatives.
![]()
![]() is called the
is called the ![]() and the variable
and the variable ![]() is the
is the ![]()
Fundamental formulas
![]()
![]()
![]() with
with ![]() a constant
a constant
![]()
![]()
![]()
![]() with
with ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Problem 1:
Solve: ![]()
We know that ![]()
From ![]() we can do some inspection
we can do some inspection
![]()
We get
(1) 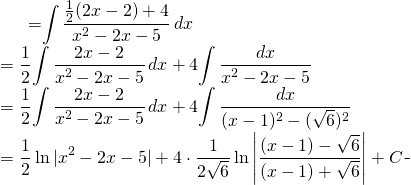
Finally:
![]()
Problem 2:
Solve: ![]()
We know that ![]()
From ![]() we can do some inspection
we can do some inspection
![]()
We get
(2) 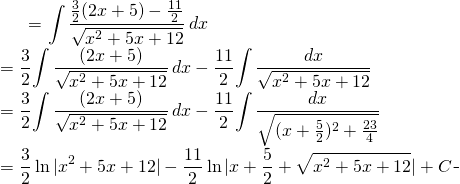
Finally:
![]()


Be the first to comment