
Integration Techniques, multiple pages
In this chapter, we are going to take off the gloves and work harder on the techniques used to solve integral problems.
We will still remain in the area of the indefinite integrals until we complete covering topics like substitution, trigonometrics and hyperbolic functions without omtitting our favorite integration by parts.
This chapter will involve more practice, including videos of some of the solutions.
Tha ability to solve integral equation depends very much on vision, planning and understanding of the concepts.
1.The method of substitution
We start with the method of substitution that we’ll use most of the time.
When we have ![]() , we often replace the variable
, we often replace the variable ![]() with a new variable
with a new variable ![]() or
or ![]() by means of
by means of ![]() .
.
![]() yielding
yielding ![]() . This technique helps us get the basic forms discussed in the previous chapter.
. This technique helps us get the basic forms discussed in the previous chapter.
Let’s investigate some of the forms.
Example:
Problem 3:
Evaluate ![]()
Let ![]()
We get the following form:
(1) 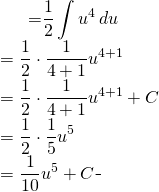
Getting back to the initial variable:
![]()
Problem 4:
Evaluate ![]()
Let ![]()
We get the following form:
![]()
Getting back to the initial variable:
![]()
Problem 5:
Evaluate ![]()
Let ![]()
We get the following form:
(2) 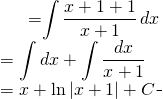
Finally:
![]()
Problem 6:
Evaluate ![]()
No substitution necessary here.
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle \int \frac{x^{2}-6\sqrt[3]{x}}{x} \, dx}&={\displaystyle \int \frac{x^{2}}{x}\, dx}-{\displaystyle 6\int \frac {\sqrt[3]{x}}{x}\, dx}\\ &= {\displaystyle \int x\, dx}-{\displaystyle 6\int \frac {x^{\frac{1}{3}}}{x^{\frac{3}{3}}}\, dx}\\ &={\displaystyle \int x\, dx}-{\displaystyle 6\int x^{\frac{1}{3}} \cdot x^{\frac{-3}{3}}\, dx}\\ &={\displaystyle \int x\, dx}-{\displaystyle 6\int x^{\frac{-2}{3}}\, dx}\\ &={\displaystyle \frac{x^{2}}{2}-6\frac{x^{\frac{1}{3}}}{\frac{1}{3}}}+C \\ &={\displaystyle \frac{x^{2}}{2}-6\frac{x^{\frac{1}{3}}}{\frac{1}{3}} }+C\\ &={\displaystyle \frac{x^{2}}{2}-18 x^{\frac{1}{3}}}+C \\ &={\displaystyle \frac{x^{2}}{2}-18 \sqrt[3]{x} }+C \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-7c4598e3a73f0b6324b5f7da6b756c23_l3.png)
Finally:
![]()
Problem 7
Evaluate: ![]()
We know that ![]()
From ![]()
![]()
We can write
(4) 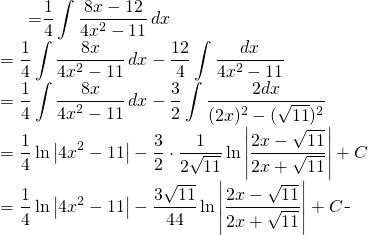
Finally we have:
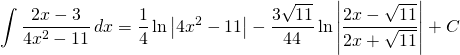
Problem 8
Evaluate: ![]()
![]()
Let ![]()
We get:
![]()
(5) 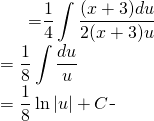
Now back to ![]() :
:
Finally:
![]()
Problem 9
Evaluate: ![]()
(6) 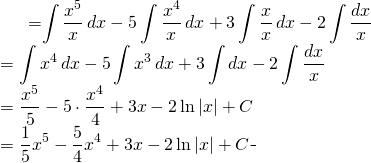
Finally:
![]()
Problem 10
Evaluate: ![]()
We’ll use substitution:
Let ![]()
(7) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle \int \frac{x^{2}}{\sqrt[4]{x^{3}+2}}\, dx}&={\displaystyle \frac{1}{3} \int \frac{3x^{2}}{\sqrt[4]{x^{3}+2}}\, dx}\\ &={\displaystyle \frac{1}{3} \int \frac{du}{\sqrt[4]{u}}}\\&={\displaystyle \frac{1}{3} \int u^{-\frac{1}{4}}du}\\ &=\frac{1}{3}\cdot \frac{u^{-\frac{1}{4}+\frac{4}{4}}}{-\frac{1}{4}+\frac{4}{4}}+C\\&=\frac{4}{9}u^{\frac{3}{4}}+C \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-165c64f06741140b89bf94a8aa8bfeaa_l3.png)
Back to ![]()
(8) ![]()
Finally:
![]()
Problem 11
Evaluate: ![]()
Let ![]()
We can now write:
(9) 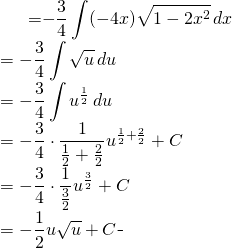
Back to ![]()
![]()
Finally:
![]()
Problem 12
Evaluate: ![]()
(10) 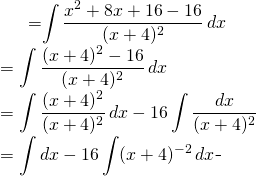
But we notice that ![]()
We get:
(11) 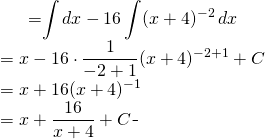
This result can be broken to show how dangerous it is to dismiss results of indefinite integrals involving constants.
(12) 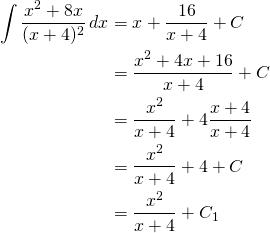
Finally:
![]()


Be the first to comment