Techniques d’Intégration , pages multiples
Ce chapitre va approfondir notre connaissance sur les calculs de primitives.
Dans ce chapitre nous verrons les techniques comme sustitution, integration des fonctions trigonométriques et hyporboliques, sans oublier mon favori, l’intégration par parties
Nous utilserons des videos dans certains des cas pour avoir toute la pratique de ces techniques.
Pour effectuer des calculs d’intégration il nous faut une bonne vision, un bon planning et une bonne comprehension du sujet.
1.Méthode de substitution
Nous commencerons par la méthode de substitution que nous utiliserons pour la plupart du temps.
Quand nous avons ![]() , on remplace souvent la variable
, on remplace souvent la variable ![]() par une autre variable
par une autre variable ![]() ou
ou ![]() par
par ![]() .
.
![]() qui donne
qui donne ![]() . Cette technique permet d’ailleurs de démontrer quelques formules vues dans le chapitre précédent.
. Cette technique permet d’ailleurs de démontrer quelques formules vues dans le chapitre précédent.
Voyons quelques exemples.
Exemple:
Problème 3:
Evaluer ![]()
Soit ![]()
On obtient la forme suivante:
(1) 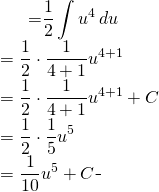
Revenant à la variable initiale:
![]()
Problème 4:
Evaluer ![]()
Let ![]()
Nous obtenons la forme suivante:
![]()
Revenant à la variable initiale :
![]()
Problème 5:
Evaluer ![]()
Let ![]()
Nous obtenons la forme suivante:
(2) 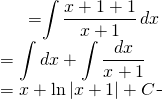
Finalement:
![]()
Problème 6:
Evaluer ![]()
Pas de substitution ici.
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle \int \frac{x^{2}-6\sqrt[3]{x}}{x} \, dx}&={\displaystyle \int \frac{x^{2}}{x}\, dx}-{\displaystyle 6\int \frac {\sqrt[3]{x}}{x}\, dx}\\ &= {\displaystyle \int x\, dx}-{\displaystyle 6\int \frac {x^{\frac{1}{3}}}{x^{\frac{3}{3}}}\, dx}\\ &={\displaystyle \int x\, dx}-{\displaystyle 6\int x^{\frac{1}{3}} \cdot x^{\frac{-3}{3}}\, dx}\\ &={\displaystyle \int x\, dx}-{\displaystyle 6\int x^{\frac{-2}{3}}\, dx}\\ &={\displaystyle \frac{x^{2}}{2}-6\frac{x^{\frac{1}{3}}}{\frac{1}{3}}}+C \\ &={\displaystyle \frac{x^{2}}{2}-6\frac{x^{\frac{1}{3}}}{\frac{1}{3}} }+C\\ &={\displaystyle \frac{x^{2}}{2}-18 x^{\frac{1}{3}}}+C \\ &={\displaystyle \frac{x^{2}}{2}-18 \sqrt[3]{x} }+C \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-7c4598e3a73f0b6324b5f7da6b756c23_l3.png)
Finalement:
![]()
Problème 7
Evaluer: ![]()
Nous savons que ![]()
From ![]()
![]()
On peut écrire
(4) 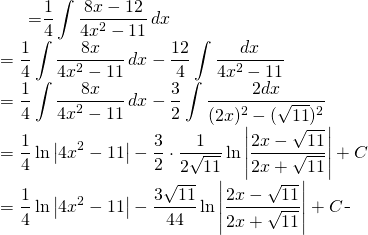
Finalement nous avons:
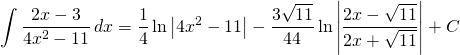
Problème 8
Evaluer: ![]()
![]()
Soit ![]()
Nous avons:
![]()
(5) 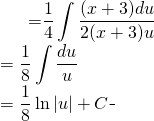
Revenant sur ![]() :
:
Finalement:
![]()
Problème 9
Evaluer: ![]()
(6) 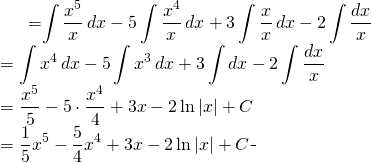
Finalement:
![]()
Problème 10
Evaluer: ![]()
Nous utiliserons la substitution:
Soit ![]()
(7) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \displaystyle \int \frac{x^{2}}{\sqrt[4]{x^{3}+2}}\, dx}&={\displaystyle \frac{1}{3} \int \frac{3x^{2}}{\sqrt[4]{x^{3}+2}}\, dx}\\ &={\displaystyle \frac{1}{3} \int \frac{du}{\sqrt[4]{u}}}\\&={\displaystyle \frac{1}{3} \int u^{-\frac{1}{4}}du}\\ &=\frac{1}{3}\cdot \frac{u^{-\frac{1}{4}+\frac{4}{4}}}{-\frac{1}{4}+\frac{4}{4}}+C\\&=\frac{4}{9}u^{\frac{3}{4}}+C \end{split} \end{equation*}](https://www.mouctar.org/wp-content/ql-cache/quicklatex.com-165c64f06741140b89bf94a8aa8bfeaa_l3.png)
De retour sur ![]()
(8) ![]()
Finalement:
![]()
Problème 11
Evaluer: ![]()
Soit ![]()
Nous avons:
(9) 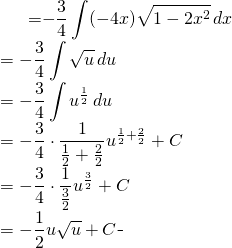
De retour sur ![]()
![]()
Finalement:
![]()
Problème 12
Evaluer: ![]()
(10) 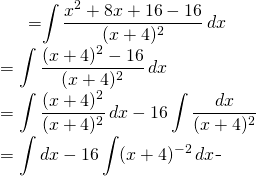
Mais nous remarquons que ![]()
Nous avons:
(11) 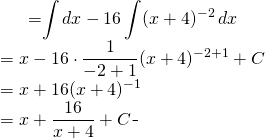
Ce résultat peut être cassé pour montrer comment c’est dangereux de rejetter une réponse du calcul des primitives sans faire des analyses.
(12) 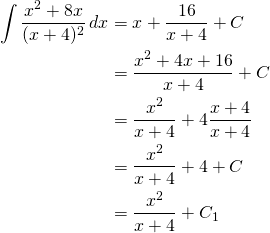
Finalement:
![]()


Be the first to comment