Techniques d’Integration , pages multiples

2.Intégration par paties

Cette technique transforme une intégrale en une autre plus facile à calculer.

La méthode vient de la formule suivante:

$(uv)'=u'v+uv'$

Ceci peut s’écrire:

$uv'=(uv)'-u'v$

Prenant la primitive des deux membres on a::

$\int udv=\int d(uv)-\int vdu$

Ou simplement:

$\int u\, dv =uv-\int v\, du$

Le choix doit être judicieux de façon à ne pas générer une autre forme plus compliquée.

Un exemple favori est le suivant:

Evaluer $\int \ln x\, dx$

Soit $u=\ln x \Rightarrow du=\frac{dx}{x}$

$dv=dx \Rightarrow v=x$

$\int \ln x\, dx=x \ln x-\int x\cdot \frac{dx}{x}=x \ln x-x+C$

Problème 13
Evaluer: $\int xe^{x}\, dx$

Soit $u=x \Rightarrow du=dx$

$dv=e^{x}dx \Rightarrow v=e^{x}$

On obtient:

(1) $\begin{equation*} \begin{split} \displaystyle \int xe^{x}\, dx}&={\displaystyle xe^{x}- \int e^{x}\, dx}\\ &={\displaystyle xe^{x}- e^{x}+C} \end{split} \end{equation*}$

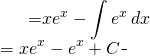
Finalement:

$\int xe^{x}\, dx=(x-1)e^{x}+C$

Problème 14
Evaluer: $\int e^{2x} \sin 3x\, dx$

Soit $u=\sin3x \Rightarrow du=3\cos 3x dx$

$dv=e^{2x}dx \Rightarrow v=\frac{1}{2}e^{2x}$

On a:

(2) $\begin{equation*} \begin{split} \displaystyle \int e^{2x} \sin 3x\, dx}& = {\displaystyle \frac{1}{2} \sin (3x) e^{2x}-\frac{1}{2}\int e^{2x} 3\cos 3x\, dx}\\ &={\displaystyle \frac{1}{2} \sin (3x) e^{2x}-\frac{3}{2}\int e^{2x} \cos 3x\, dx} \end{split} \end{equation*}$

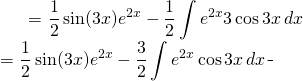
On recommence le processus:

Soit $u=\cos3x \Rightarrow du=-3\sin 3x dx$

$dv=e^{2x}dx \Rightarrow v=\frac{1}{2}e^{2x}$

(3) $\begin{equation*} \begin{split} \displaystyle \int e^{2x} \sin 3x\, dx}&={\displaystyle \frac{1}{2} \sin (3x) e^{2x}-\frac{3}{2}[\frac{1}{2} \cos (3x) e^{2x}+\frac{3}{2}\int e^{2x} \sin 3x\, dx]}\\ &= {\displaystyle \frac{1}{2} \sin (3x) e^{2x}-\frac{3}{4}\cos (3x) e^{2x}-\frac{9}{4}\int e^{2x} \sin 3x\, dx \end{split} \end{equation*}$

Une fraction de l’intégrale d’origine:

$(1+\frac{9}{4})\int e^{2x} \sin 3x\, dx}={\displaystyle \frac{1}{2} \sin (3x) e^{2x}-\frac{3}{4}\cos (3x) e^{2x}+C$

$\frac{13}{4}\int e^{2x} \sin 3x\, dx}={\displaystyle \frac{1}{2} \sin (3x) e^{2x}-\frac{3}{4}\cos (3x) e^{2x}+C$

$\int e^{2x} \sin 3x\, dx}={\displaystyle \frac{2}{13} \sin (3x) e^{2x}-\frac{3}{13}\cos (3x) e^{2x}+C$

$\int e^{2x} \sin 3x\, dx}={\displaystyle \frac{e^{2x}}{13} (2\sin 3x -3\cos 3x )+C$

Finalement:

$\int e^{2x} \sin 3x\, dx}={\displaystyle \frac{e^{2x}}{13} (2\sin 3x -3\cos 3x )+C$

Problème 15
Evaluer: $\int \sin^{-1} x\, dx$

Soit $u=\sin^{-1} x \Rightarrow du=\frac{dx}{\sqrt{1-x^{2}}}$

$dv=dx \Rightarrow v=x$

On écrit:

(4) $\begin{equation*} \begin{split} \displaystyle \int \sin^{-1} x\, dx}&={\displaystyle x sin^{-1} x- \int \frac{x}{\sqrt{1-x^{2}}} \, dx}\\ &={\displaystyle x sin^{-1} x+ \frac{1}{2} \int \frac{-2x}{\sqrt{1-x^{2}}}}\\ &={\displaystyle x sin^{-1} x-\sqrt{1-x^{2}}+C \end{split} \end{equation*}$

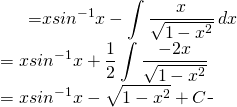
Finalement:

$\int \sin^{-1} x\, dx}={\displaystyle x sin^{-1} x-\sqrt{1-x^{2}}+C$

Problème 16
Evaluer: $\int e^{x} \cos x\, dx$

Soit $u=e^{x} \Rightarrow du=e^{x}\, dx$

$dv=\cos x\,dx \Rightarrow v=\sin x$

On écrit:

$\int e^{x} \cos x\, dx}={\displaystyle e^{x} \sin x - \int e^{x} \sin x\, dx$

On recommence:

Soit $u=e^{x} \Rightarrow du=e^{x}\, dx$

$dv=\sin x\,dx \Rightarrow v=-\cos x$

Revenant à l’équation d’origine:

$\int e^{x} \cos x\, dx}={\displaystyle e^{x} \sin x -[-e^{x} \cos x + \int e^{x} \cos x\, dx]$

$\int e^{x} \cos x\, dx}={\displaystyle e^{x} \sin x + e^{x} \cos x - \int e^{x} \cos x\, dx$

$2\int e^{x} \cos x\, dx}={\displaystyle e^{x} \sin x + e^{x} \cos x + C$

$\int e^{x} \cos x\, dx}={\displaystyle \frac{e^{x}}{2}( \sin x + \cos x )+ C$

Finalement:

$\int e^{x} \cos x\, dx}={\displaystyle \frac{e^{x}}{2}( \sin x + \cos x )+ C$

Problème 17- Cas Spécial
Evaluer: $\int \sec^{n} x \, dx$

Quand $n$ est un grand nombre naturel, on réduit $n$ par $2$ pour créer une situation où on doit intégrer $\sec^{2} x$

Nous posons:

Soit $u=\sec^{n-2}x \Rightarrow du=(n-2)\sec^{n-2} x \tan x \, dx$

$dv=\sec^{2} x \,dx \Rightarrow v=\tan x$

Nous avons:

$\int \sec^{n} x \, dx} ={\displaystyle \sec^{n-2}x \tan x- (n-2) \int \sec^{n-2} x \tan^{2} x \, dx$

Ou:

$\int \sec^{n} x \, dx} ={\displaystyle \sec^{n-2}x \tan x- (n-2) \int \sec^{n-2} x (\sec^{2} x-1) \, dx$

$\int \sec^{n} x \, dx} ={\displaystyle \sec^{n-2}x \tan x- (n-2) \int \sec^{n} x \, dx+ (n-2) \int \sec^{n-2} x \, dx$

Nous retrouvons l’intégrale d’origine à droite. On regroupe et on obtient:

$(n-2+1)\int \sec^{n} x \, dx} ={\displaystyle \sec^{n-2}x \tan x+ (n-2) \int \sec^{n-2} x \, dx$

$(n-1)\int \sec^{n} x \, dx} ={\displaystyle \sec^{n-2}x \tan x+ (n-2) \int \sec^{n-2} x \, dx$

Nous avons:

$\int \sec^{n} x \, dx} ={\displaystyle \frac{ \sec^{n-2}x \tan x}{n-1}+\frac{n-2}{n-1} \int \sec^{n-2} x\, dx$

Formule utile pour la suite:

$\int \sec x \, dx} ={\displaystyle \ln |\sec x+ \tan x | +C$

Problème 18
Evaluer: $\int \sec^{5} x \, dx$

Soit $u=\sec^{5-2}x \Rightarrow du=(5-2)\sec^{5-2} x \tan x \, dx$

Ou bien:

$u=\sec^{3}x \Rightarrow du=3\sec^{3} x \tan x \, dx$

$dv=\sec^{2} x \,dx \Rightarrow v=\tan x$

Nous obtenons:

$\int \sec^{5} x \, dx} = {\displaystyle \frac{1}{4}\sec^{3}x \tan x +\frac{3}{4} \int \sec^{3} x \, dx$

Juste pour blaguer:

$\int \sec^{3} x \, dx} ={\displaystyle \int \sec^{2} x \sec x \, dx$

Soit $u=\sec x \Rightarrow du=\sec x \tan x \, dx$

$dv=\sec^{2} x \,dx \Rightarrow v=\tan x$

$\int \sec^{3} x \, dx} ={\displaystyle \sec x \tan x-\int \sec x \tan x \tan x \,dx$

$\int \sec^{3} x \, dx}={\displaystyle \sec x \tan x-\int \sec x \tan^{2} x \,dx$

$\int \sec^{3} x \, dx}={\displaystyle \sec x \tan x-\int \sec x (\sec^{2} x-1) \,dx$

$\int \sec^{3} x \, dx}={\displaystyle \sec x \tan x-\int \sec^{3} x+ \int \sec x \,dx$

$2\int \sec^{3} x \, dx}={\displaystyle \sec x \tan x+ \int \sec x \,dx$

$2\int \sec^{3} x \, dx}={\displaystyle \sec x \tan x+ \ln| \sec x + tan x |+C$

$\int \sec^{3} x \, dx}={\displaystyle \frac{1}{2}(\sec x \tan x+ \ln| \sec x + tan x |)+C$

Revenant à l’équation d’origine:

$\int \sec^{5} x \, dx} = {\displaystyle \frac{1}{4}\sec^{3}x \tan x +\frac{3}{4}\cdot \frac{1}{2}(\sec x \tan x+ \ln| \sec x + tan x |)+C$

$\int \sec^{5} x \, dx} = {\displaystyle \frac{1}{4}\sec^{3}x \tan x +\frac{3}{8}(\sec x \tan x+ \ln| \sec x + tan x |)+C$

Finalement:

$\int \sec^{5} x \, dx} = {\displaystyle \frac{1}{4}\sec^{3}x \tan x +\frac{3}{8}(\sec x \tan x+ \ln| \sec x + tan x |)+C$

1 2 3 4 5 6 7

Post Views: 834

2.Intégration par paties

$\int u\, dv =uv-\int v\, du$

Be the first to comment

Leave a Reply Cancel reply