3. Substitution trigonométrique
Les expressions algébriques qui suivent nécessitent la méthode de substitution trigonométrique:
![]()
![]()
![]()
Cas trigonométriques
| Integral Involving | Use Substitution | Then Identity |
>
Ou Substitution Hyperbolique :
| Integral Involving | Use Substitution | Then Identity |
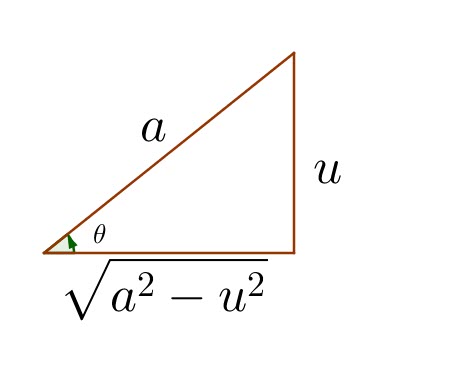
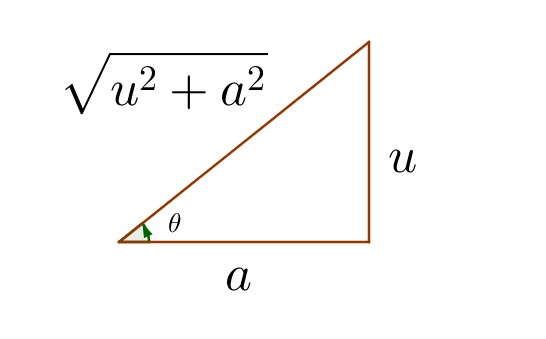
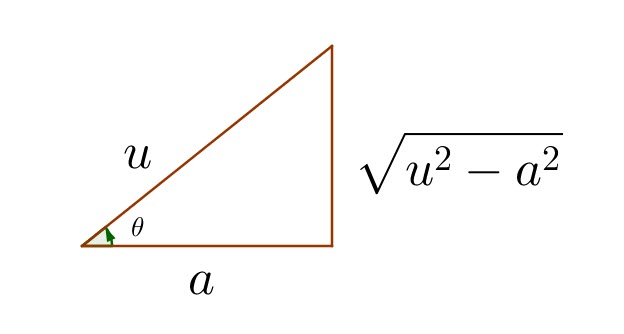
Problème 19
Evaluer: ![]()
Nous retrouvons ![]()
Dans ce cas, ![]()
Soit ![]()
![]()
![]()
De retour à l’équation:
(1) 
Maintenant calculons ce qui suit:
![]()
Combinant avec les méthodes connues:
(2) 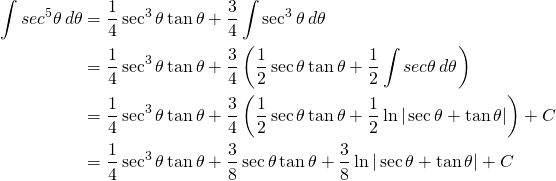
De retour sur ![]() on applique ce qui suit:
on applique ce qui suit:
![]()
![]()
![]()
![]()
![]()
En appliquant au résultat:
![]()
(3) 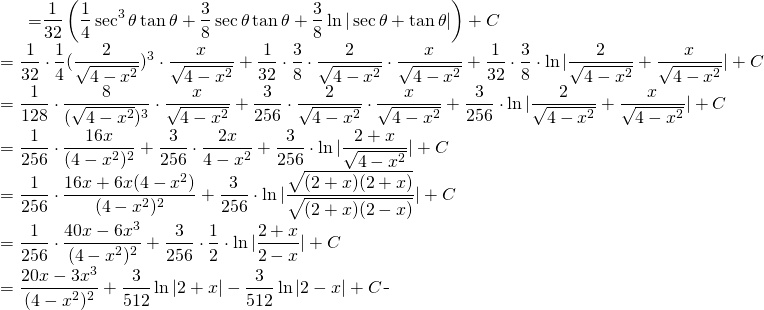
Finalement:
![]()
Problème 20
Evaluer: ![]()
Ce cas contient ![]()
Dans ce cas, ![]()
Ici ![]()
Soit ![]()
![]()
![]()
De retour sur l’équation
(4) 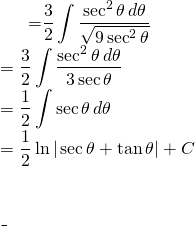
De retour sur ![]()
![]()
![]()
![]()
(5) 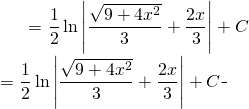
Finalement:
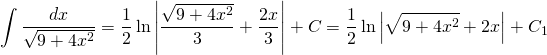
Ou bien:
![]()
En utilisant simplement la substitution hyperbolique:
Ici ![]()
Soit ![]()
Nous avonst ![]()
![]()
On remplace:
(6) 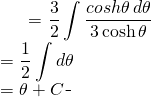
Mais nous avons vu que:
![]()
Alors:
![]()
Problème 21
Evaluate: ![]()
Ce cas contient ![]()
Ici, ![]()
Alors ![]()
Soit ![]()
![]()
![]()
De retour sur l’équation
(7) 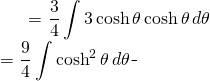
Mais nous savons que:
![]()
![]()
(8) 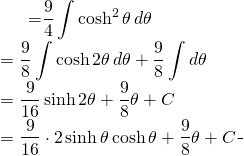
De retour sur ![]()
![]()
![]()
Sur l’équation d’origine:
(9) ![]()
![]()
Finalement:
![]()
OU:
![]()
Problème 22
Evaluer: ![]()
Avec la substitution trigonométrique
Ce cas contient ![]()
Ici, ![]()
Alors ![]()
Soit ![]()
![]()
![]()
![]()
![]()
De retour sur l’équation
(10) 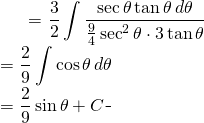
![]()
![]()
Nous obtenons:
![]()
Finalement:
![]()
Problème 23
Evaluer: ![]()
Utilisant la substitution hyperbolique
Ce cas contient ![]()
Ici, ![]()
Alors ![]()
Soit ![]()
![]()
![]()
![]()
![]()
De retour sur l’équation
(11) 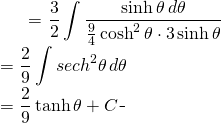
![]()
![]()
![]()
![]()
Sur l’équation d’origine:
![]()
Finalement:
![]()


Be the first to comment