4.Intégration avec des quadratiques au dénominator
C’est la forme:
![]()
Quelques formules de rappel:
Nous avons les vidéos.
![]()
![]()
Nous savons que
![]()
![]()
Ces formules nous serviront ici.
![]() peut se mettre sous l’une des formes:
peut se mettre sous l’une des formes:
![]() OU
OU ![]() en fonction du signe de
en fonction du signe de ![]()
Ce qui nous permet d’utiliser l’une ou l’autre de ces formules.
Problème 24
Evaluer:
![]()
Prenons soins de la quadratique:
![]()
On applique notre formule:
(1) 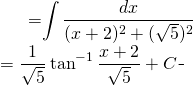
Finalement:
![]()
Problème 25
Evaluer:
![]()
Nous pouvons écrire:
![]()
Soit:
![]()
![]()
De retour sur ![]()
![]()
Finalement:
![]()
Problème 26
Evaluer:
![]()
On peut écrire:
![]()
Soit:
![]()
![]()
De retour sur ![]()
![]()
Finalement:
![]()
Problème 27
Evaluer: ![]()
Ce cas contient ![]()
Ici, ![]()
Alors ![]()
Let ![]()
![]()
![]()
De retour sur l’équation
(2) 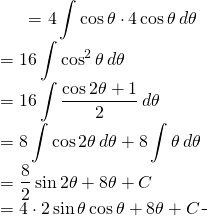
Mais nous savons que:
![]()
![]()
![]()
De retour sur l’équation:
(3) 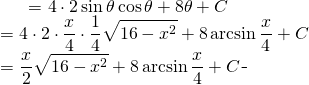
Finalement:
![]()


Be the first to comment